Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Проверим каждое из утверждений.
1) «Против большей стороны треугольника лежит больший угол» — верно, по свойству треугольника.
2) «Любой прямоугольник можно вписать в окружность» — верно; выпуклый четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов этого четырёхугольника равна 180°.
3) «Площадь треугольника меньше произведения двух его сторон» — верно, поскольку площадь треугольника можно вычислить по формуле 
, где a и b — стороны треугольника, а 
— угол между этими сторонами. Так как 
не может быть больше 1, то и S не может превышать полупроизведения сторон.
Видео:Напротив большей стороны лежит больший уголСкачать
Четвертый признак равенства треугольников
Четвертый признак равенства треугольников — это признак,
c помощью которого можно доказать, что треугольники равны.
С помощью четвертого признака равенства можно решить
любую из задач, где требуется доказать, что треугольники равны.
Формулировка:
Если две стороны и угол, лежащий против большей из сторон
одного треугольника соответственно равны двум сторонам и углу,
лежащему против большей из сторон другого треугольника,
то такие треугольники равны.
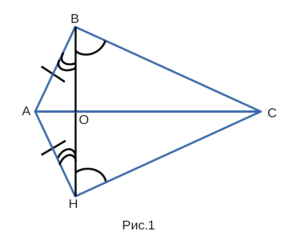
Докажем, что △ABC и △FHE равны между собой. Для этого
совместим их так, как показано на рисунке 1.
Доказательство:
- Рассмотрим △ABC и △FHE, которые наложились друг на друга,
AВ = AH,∠ABO = ∠AHO, ∠BOC = ∠HOC. Докажем, что △ABC = △FHE. - △ABH — равнобедренный (AB = AH), значит ∠ABO = ∠AHO.
- ∠BOC = ∠HOC, так как остатки равных углов.
- △BHC — равнобедренный(∠BOC = ∠HOC), а так как углы при боковых
сторонах HC и BC равны, значит HC = BC. - Итак, △ABC = △FHE по двум сторонам и углу, лежащему
против большей из сторон.
Видео:Почему напротив большей стороны в треугольнике лежит больший угол?Скачать
Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника помогают сравнивать углы треугольника, зная соотношение его сторон, и наоборот.
(соотношения между сторонами и углами треугольника).
В треугольнике:
1) против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
1) Дано : ∆ ABC, AC>AB.
Отложим на стороне AC отрезок AK: AK=AB.
Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.
Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.
Значит, у него углы при основании равны: ∠ABK=∠AKB.
Для треугольника BCK ∠AKB — внешний.
Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.
angle ABK\ angle ABK = angle AKB\ angle AKB > angle C end right> Rightarrow angle ABC > angle C.]» title=»Rendered by QuickLaTeX.com»/>
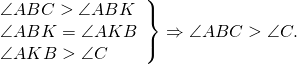
(методом от противного).
Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо AC
Если AC=AB, то треугольник ABC — равнобедренный с основанием BC и у него углы при основании равны: ∠B=∠C, что противоречит условию.
По доказанному в пункте 1), против большей стороны лежит больший угол. Поэтому, если AC
Значит, выдвинутое нами предположение неверно. Следовательно, AC>AB.
Что и требовалось доказать .
Видео:Почему в треугольнике против большей стороны - больший угол ➜ ДоказательствоСкачать
2 Comments
опечатка!
В треугольнике:
1) против большей стороны лежит больший угол;
1) против большего угла лежит большая сторона.
📸 Видео
Соотношения между сторонами и углами треугольника. 7 класс.Скачать
Против большей стороны треугольника лежит больший угол. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать
Против большего угла лежит большая сторона.Скачать
Против большей стороны лежит больший угол, против большего угла лежит большая сторонаСкачать
Найдите угол: задача по геометрииСкачать
Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать
В треугольнике против большей стороны лежит ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать
Как я использую дюймы в пэчворке и не пересчитываюСкачать
7 класс. Глава5. Против большей стороны лежит больший уголСкачать
Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать
Неравенство треугольникаСкачать
SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать
Теорема о большей стороне | Задачи 1-8 | Решение задач | Волчкевич | Уроки геометрии в задачах 7-8Скачать
📒«Соотношения между сторонами и углами треугольника» Геометрия 7 класс 📒Скачать
