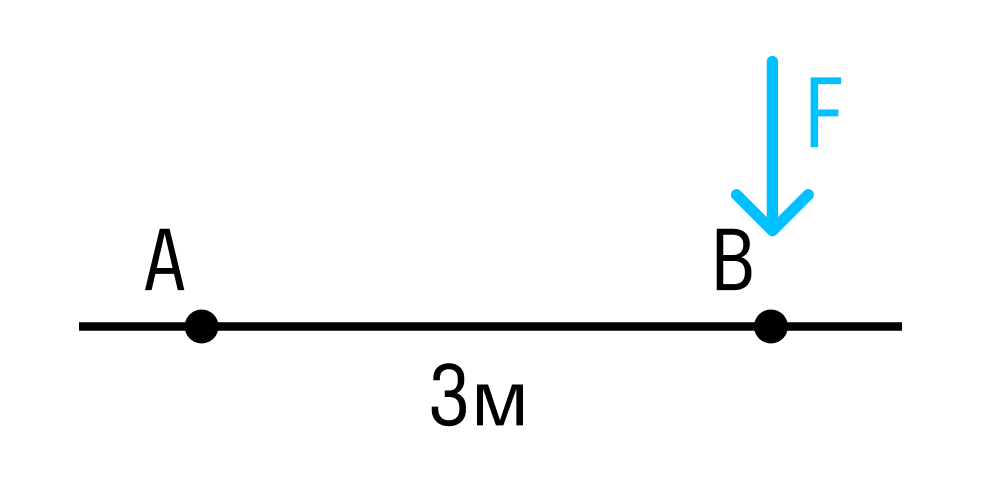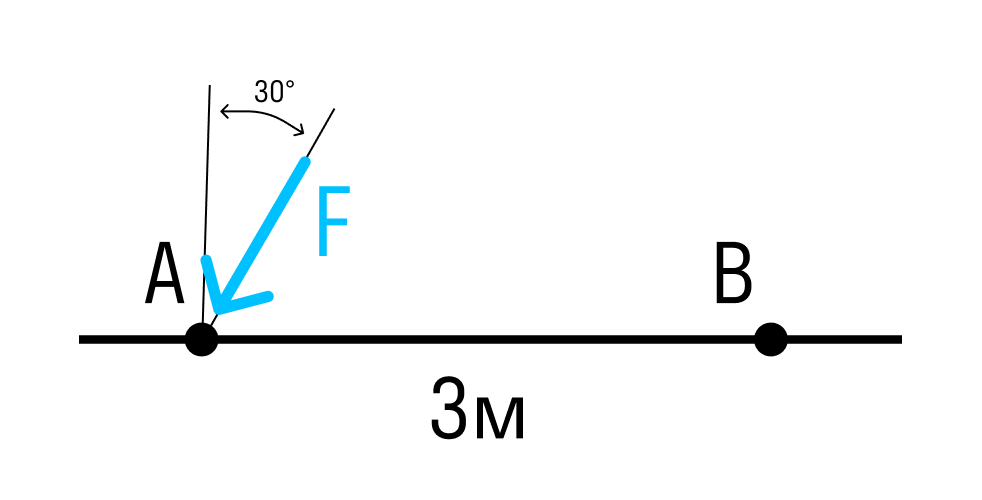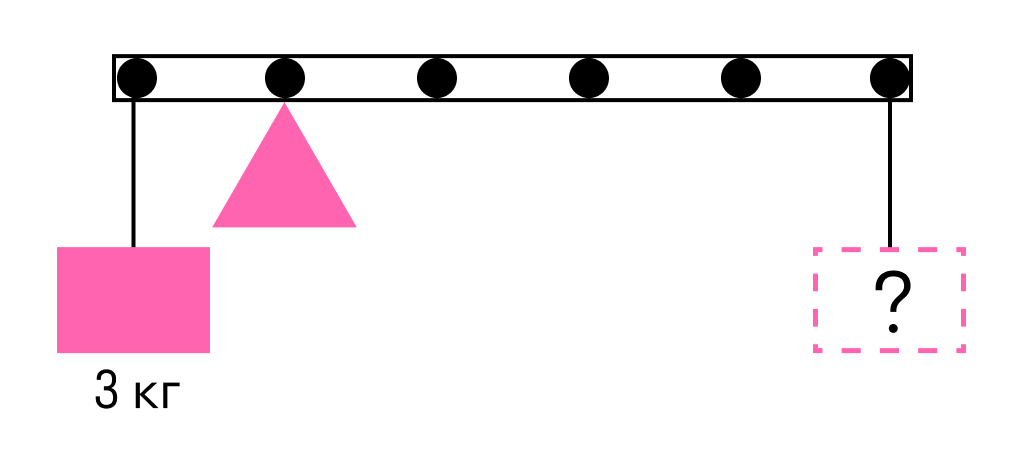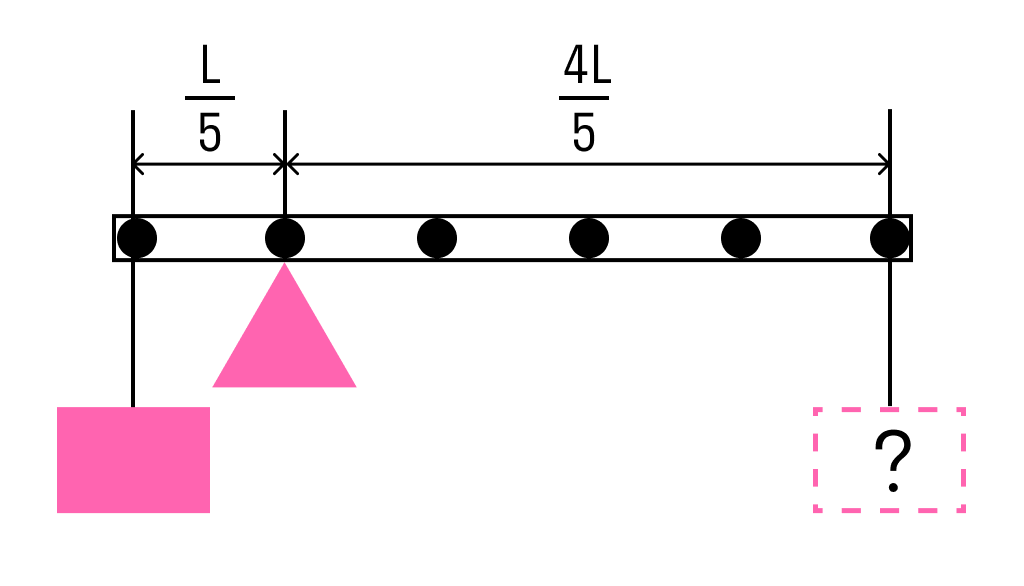Нарисовать вектор тормозящей силы (6 видео)

лабораторных работ по физике

Сборник

Вопросов и задач для самостоятельной подготовки к защите

лабораторных работ по физике

Раздел 1 «Механика»

(для студентов всех специальностей)

Настоящий сборник является первой частью «Сборника вопросов и задач для самостоятельной подготовки к защите лабораторных работ по общей физике» и содержит билеты к лабораторным работам №1, №2, №5, №10. В каждом билете содержится один теоретический вопрос и одна задача.

Нумерация работ соответствует принятой на кафедре физики МГУПП.

ЛАБОРАТОРНАЯ РАБОТА 1

ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТЕЛ ПРАВИЛЬНОЙ

1. Расскажите о штангенциркуле и о проведении измерений с помощью этого прибора.

2. Вычислить объем шара, если его радиус R= (15,73 + 0,02) мм.

1. Расскажите о микрометре и о проведении измерений с помощью этого прибора.

2. Вычислить предельную абсолютную погрешность измерения плотности куба, если его ребро a = (10,12 + 0,08) мм, а масса m = (7,3 + 0,1) г.

1. Каким образом определяется погрешность прямых измерений? В каком виде записывается окончательный результат измерения, и каков физический смысл такой записи?

2. Найти площадь квадрата, если его сторона a = (24,2 + 0,3) мм. Чему равна относительная погрешность измерения площади квадрата?

1. Что называется ценой деления, точностью прибора? Как можно определить эти величины? Чему равна приборная погрешность инструментов, которыми Вы пользовались?

2. Вычислить предельную абсолютную погрешность измерения плотности цилиндра, если его объем V = (105 + 1) ×10 2 мм 3 , а масса m = (85,2 + 0,6) г.

1. Какие погрешности называют систематическими, случайными? Как они возникают?

2. Найти плотность материала куба, если его масса m = (1,50 + 0,02) г, высота ребра h = (5,91 + 0,01) мм.

1. Какие измерения называются прямыми? Как определяется предельная погрешность этих измерений? Как правильно записывается результат этих измерений? Приведите примеры.

2. Определить относительную погрешность измерения площади шара, если его радиус R = (8,80 + 0,02) см.

1. Какие измерения называются косвенными? Как определяется абсолютная и относительная погрешности этих измерений?

2. Найти площадь боковой поверхности цилиндра, если радиус его основания R = (38,4 + 0,8) мм, а высота h = (80,1 + 0,9) мм.

1. Какая величина называется предельной относительной погрешностью результата измерения? С какой целью вводится эта величина? Какие численные значения e допустимы в лабораторных измерениях?

2. Определить предельную относительную погрешность измерения объема куба, если его ребро 15,3 см, приборная погрешность 0,05 см, а средняя абсолютная погрешность 0,03 см.

1. Как проводятся измерения приборами, снабженными нониусом? Какова была приборная погрешность штангенциркуля, которым Вы пользовались при выполнении этой лабораторной работы?

2. Найти объем конуса, если радиус основания R = (15,22 + 0,04) см, а высота h = (48,1 + 0,8) см.

1. Как определяется объем кольца? Как вычислялись относительная и абсолютная погрешности объема кольца?

2. Найти объем параллелепипеда, если его основанием является квадрат со стороной a = (22,4 + 0,6) мм, а его высота h = (88,8 + 0,8) мм.

1. Какая величина называется плотностью вещества? В каких единицах она измеряется в системе СИ?

2. Найти объем цилиндра, если радиус основания R = (58,4 + 0,5) мм, а высота его равна h = (122,8 + 0,2) мм.

1. Как определяется предельная абсолютная погрешность прямых измерений? Приведите примеры из лабораторной работы 1.

2.Найти плотность материала пирамиды, если ее объем

V = (118 + 2)×10 2 мм 3 , а ее масса m = (93,4 + 0,7) г.

1. Какие погрешности называют систематическими, случайными? Какова природа возникновения этих ошибок, и как они учитываются в лабораторной работе 1?

2. Найти площадь ромба, если его сторона a = (31,4 + 0,9) мм, а высота h = (56,4 + 0,2) мм.

1. Какие измерения называются косвенными? Как определяются абсолютная и относительная погрешности этих измерений? Приведите примеры таких измерений из лабораторной работы 1.

2. Найти площадь параллелепипеда, если его основанием является прямоугольник со сторонами a = (14,3 + 0,5) мм и b = (18,6 + 0,8) мм, а его высота h = (34,6 + 0,1) мм.

1. Как определяются предельная абсолютная и относительная погрешности прямых измерений? Приведите примеры из лабораторной работы 1.

2. Вычислить площадь боковой поверхности куба, если его ребро h = (39,2 + 0,8) мм.

ЛАБОРАТОРНАЯ РАБОТА 2

ИССЛЕДОВАНИЕ ЗАКОНОВ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ И ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ

1.Как в работе проверялась формула скорости равноускоренного движения?

2. Тело массой 200 г падает вертикально вниз с ускорением 920 см/с 2 . Чему равна сила сопротивления воздуха?

1. Как в работе проверялось соотношение V₁:V₂:V₃ = t₁:t₂:t₃? Откуда оно следует?

2. Чему равен вес человека, который равноускоренно начал подниматься в лифте с ускорением 1 м/с 2 . Масса человека 70 кг.

1. Как в работе осуществлялась проверка основного закона динамики материальной точки?

2. Найти ускорение, с которым будут двигаться грузы с

массами m и 3m. Массами блока и нитей пренебречь,

трение не учитывать.

Ответ: 4,9 м/с 2 .

m 3m

1. Как в работе осуществлялась проверка формулы пути равноускоренного движения?

2. Тело скользит равномерно по наклонной плоскости с углом наклона45°. Определить коэффициент трения тела о плоскость.

2. Тело брошено горизонтально с некоторой высоты со скоростью 20 м/с. Какова его скорость через 2 с?

1. Напишите уравнение движения и формулу скорости для равно-

переменного движения. Какая величина называется мгновенной скоростью и ускорением? Как определяется средняя скорость движения?

2. Массы грузов соответственно равны m₁ = 1,5 кг,

m₂ = 0,5 кг. Груз 2 удерживался электромагнитом.

После его отключения система пришла в движение.

Найти ускорение грузов. Трением в блоке и массой блока пренебречь.

Ответ: 4,9 м/с 2

m₁

m₂

Билет 7.

1. В каком движении участвуют грузы при выключении магнита? Как меняется их движение при прохождении одним из грузов первой платформы? Напишите уравнения этих движений и постройте графики зависимости скорости от времени.

2. Чему равен вес человека, который равноускоренно начал опускаться в лифте с ускорением 1 м/с 2 ? Масса человека 70 кг.

Билет 8.

1. Сформулируйте 3 – й закон Ньютона. Чем отличается сила тяжести от веса тела?

2.Уравнение движения тела имеет вид: x = (5t + 0,8t 2 ) м. Определить среднюю скорость в интервале времени от 2 с до 5 с.

Билет 9.

1. Во второй части работы проверялось соотношение F₁t₁:F₂t₂:F₃t₃ = V₁:V₂:V₃. Откуда оно следует? Как осуществлялось изменение силы F? Какое условие должно было соблюдаться при этом?

2. Тело брошено горизонтально с некоторой высоты со скоростью 20 м/с. Каково перемещение этого тела в пространстве за 2 с от начала движения?

Билет 10.

1. Как в работе проверялось соотношение S₁:S₂:S₃ = t₁ 2 :t₂ 2 :t₃ 2 ? Откуда оно следует?

2. Тело массой 2 кг брошено вертикально вверх со скоростью V₀ = 10 м/с. На какую максимальную высоту оно поднимется если 1) трением о воздух пренебречь; 2) трение о воздух равно 5 Н?

Ответ: 5,1 м; 4,1 м.

Билет 11.

1. Что называется импульсом материальной точки? Какая величина называется импульсом системы? Сформулируйте основной закон динамики для материальной точки?

2. Уравнение движения тела имеет вид: x = (0,5t 4 – 27t 2 ) м. Через сколько времени после начала движения ускорение тела станет равно 6 м/с 2 ?

Билет 12.

1. В каком движении участвуют грузы при выключении магнита? Напишите уравнение этого движения и дайте определение величин, которые в него входят. Постройте графики зависимости координаты от времени и скорости от времени для этого вида движения.

2. Небольшой ящик тянут за веревку по гладкой поверхности (без трения). Веревка натянута под углом 45°к направлению движения. Определить величину приложенной силы, если она придает ящику ускорение 0,5 м/с 2 , масса ящика 2 кг.

Билет 13.

1. Дайте определение массы и веса, назовите единицы их измерения в системе СИ. Какую величину мы измеряем, вставая на напольные весы?

2. Мяч брошен с некоторой высоты горизонтально со скоростью 15 м/с. Найти нормальное и тангенциальное ускорения мяча через одну секунду после начала движения. Сопротивление воздуха не учитывать.

Ответ: 8,2 м/с 2 ; 5,4 м/с 2

Билет 14.

1. Какой закон динамики материальной точки называется основным? Как в работе 2 осуществлялась его проверка?

2. Тело движется вдоль оси X так, что зависимость координаты от времени задано уравнением x = ( 6 – 3t + 2t 2 ) м. Найти средние скорость и ускорение тела за промежуток времени от 2 до 4 с.

Ответ: 9 м/с; 4 м/с 2

Билет 15.

1. Для проверки основного закона динамики используется соотношение F₁t₁:F₂t₂:F₃t₃ = V₁:V₂:V₃. Из какого уравнения находились скорости V₁, V₂, V₃? Откуда оно следует?

2. Автомобиль массой 1 т поднимается по шоссе с уклоном 30° под действием силы тяги 7 кН. Найти ускорение автомобиля, если коэффициент трения равен 0,1.

ЛАБОРАТОРНАЯ РАБОТА 5

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА

Билет 1.

1.Как в лабораторной работе осуществлялась проверка соотношения М₁/М₂ =e₁/e₂ ?

2. Шкив диаметром 20 см делает 300 оборотов за 5 мин. Определить период вращения шкива, угловую и линейную скорости на ободе шкива.

Ответ: 1с; 6,28 рад/с; 0,628 м/с.

Билет 2.

1. Как связаны линейные и угловые скорости и ускорения точки, движущейся по окружности?

2. Найти радиус вращающегося колеса, если известно, что линейная скорость точек, лежащих на ободе, в 2,5 раза больше линейной скорости точек, лежащих на 5 см ближе к оси колеса.

Ответ: 8,3 см.

Билет 3.

1.Напишите зависимость угла поворота и угловой скорости от времени при равноускоренном и равнозамедленном движении материальной точки по окружности.

2. Нарисуйте вектор тормозящей силы, действующей на

обод вращающего колеса, и постройте вектор момента

этой силы относительно точки О, лежащей на оси

1. Запишите основной закон динамики для твердого тела, вращающегося вокруг неподвижной оси.

2. Вал начинает вращаться и за первые 10 с совершает 50 оборотов. Считая вращение вала равноускоренным, определите угловое ускорение и угловую скорость вала через 10 с после начала вращения.

Ответ: » 6,28 рад/с 2 ; » 62,8 рад/с

Билет 5.

1. Как в работе рассчитывались моменты инерции дополнительных грузов I_г1, I_г2?

2. Точка А вращается равноускоренно под действием силы .

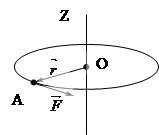
Показать направление момента силы

относительно точки О, лежащей на оси вращения, и

направления векторов d , и точки А. Написать

уравнение движения точки А.

1. Как в работе рассчитывалось линейное ускорение опускающегося груза и угловое ускорение крестовины?

2. Колесо при вращении имеет начальную частоту 5 с –1 , после торможения в течение 10 с частота уменьшилась до 3 с –1 . Найти угловое ускорение колеса и число оборотов, сделанных за время торможения.

Ответ: »1,256 рад/с 2 ; 40

1. Как в работе рассчитывается момент силы, действующей на крестовину, относительно оси вращения крестовины?

2. Точка А вращается равнозамедленно по окружности

в направлении, указанном стрелкой.

Показать направление угловой и линейной скорости,

а также углового и линейного ускорения точки А.

Написать уравнение движения точки А.

1. Как в работе рассчитывается угловое ускорение крестовины?

2. Построить вектор линейной скорости и линейного

ускорения точки А, вращающейся по окружности

с центром в точке О, если на рисунке показано

направление угловой скорости точки А. Движение

точки А – ускоренное.

1. Как будет изменяться момент инерции крестовины с дополнительными грузами, если грузы переместить дальше от оси вращения?

2. Построить вектор момента импульса (относительно точки

О) материальной точки А, вращающейся по окружности

с центром в точке О в направлении, указанном стрелкой.

Написать уравнение движения точки А, считая движение

1. Как рассчитывается момент импульса твердого тела, вращающегося вокруг неподвижной оси?

2.Колесо вращается по закону j = А + Bt – Ct 3 , где А = 4 рад, В = 5 рад/с,

С = 1 рад/с 3 . Найти для момента времени t = 1 с угловую скорость колеса, линейную скорость и полное ускорение точек, лежащих на ободе колеса. Радиус колеса 2 см.

Ответ: 2 рад/с; 0,04 м/с; 0,14 м/с 2

1. Как рассчитывается момент силы относительно точки и относительно оси? Под действием момента какой силы вращалась крестовина при опускании груза?

2. Зависимость угловой скорости от времени для вращающегося тела имеет вид w = A + Bt, где А = 2 рад/с, В = 0,5 рад/с 2 . Найти полное число оборотов, совершенное телом за 20 с после начала вращения.

Ответ: 22 оборота.

1.Как рассчитывают момент импульса материальной точки относительно неподвижной точки и момент импульса твердого тела относительно не- подвижной оси?

2. Материальная точка движется по окружности радиусом 81 см согласно уравнению S = At 3 , где А = 2 м/с 3 . В какой момент времени нормальное ускорение точки будет равно тангенциальному? Чему будет равно полное ускорение точки в этот момент времени?

Ответ: 0,65 с; 11 м/с 2

1. Как рассчитывается момент инерции материальной точки, твердого тела? Сформулируйте теорему Штейнера.

2. Колесо вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Ответ: 3,2 рад/с 2

1. Как формулируется основной закон динамики для тела, вращающегося относительно неподвижной точки, неподвижной оси?

2. Материальная точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением 5 см/с 2 . Через сколько времени после начала движения нормальное ускорение точки будет равно тангенциальному?

1. Рассчитайте по результатам лабораторной работы момент импульса крестовины (без дополнительных грузов) относительно ее оси вращения в момент касания грузом пола, если леска наматывалась на малый шкив.

2. Маховик, момент инерции которого равен 63,5 кг×м 2 , вращается с постоянной угловой скоростью 31,4 рад/с. Найти момент тормозящей силы, под действием которого маховик останавливается через 20 с.

Ответ: 100 Н×м

ЛАБОРАТОРНАЯ РАБОТА 10

ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА ЗАТУХАНИЯ И ПРИВЕДЕННОЙ ДЛИНЫ ФИЗИЧЕСКОГО МАЯТНИКА

1. Выведите формулу для периода колебаний математического маятника.

2. Найти максимальную скорость и максимальное ускорение материальной точки, колеблющейся по закону x = 2 sin (pt / 4 + p / 4) см.

Ответ: 1,57 см/с; 1,23см/с 2

1. Напишите уравнение свободных гармонических колебаний и его решение.

2. Определите амплитуду, период и путь, проходимый колеблющейся материальной точкой за время 1/48 с от начала движения, если колебания происходят по закону x = 10 sin (8pt + p / 6) см.

Ответ: 10 см; 0,25 с; 3,7 см.

1. Какими параметрами характеризуются затухающие колебания?

2. Логарифмический декремент затухания математического маятника равен 0,2. Во сколько раз уменьшится амплитуда колебаний за время одного колебания маятника?

Ответ: 1,22.

1. Как рассчитывается приведенная длина физического маятника?

2. На пружине подвешен груз массой 10 кг. Определить период вертикальных колебаний груза, если известно, что под действием груза массой 1 кг пружина растягивается на 0,5 см.

Ответ: 0,4 с.

1. Нарисуйте график затухающих колебаний. Какие параметры таких колебаний Вы определяли в работе?

2. Амплитуда затухающих колебаний математического маятника за первую минуту уменьшилась в два раза. Во сколько раз она уменьшится за 3 минуты от начала колебаний?

1. Напишите уравнение вынужденных колебаний и его решение.

2. Начальная фаза свободного гармонического колебания материальной точки равна нулю. Через какую долю периода скорость колеблющейся точки будет равна половине ее максимальной скорости? Колебания совершаются по закону синуса.

1. Вывести формулу для периода колебаний пружинного маятника.

2. Чему равен логарифмический декремент затухания математического маятника с длиной нити 1м, если за 1 минуту амплитуда колебаний уменьшилась в два раза?

Ответ: 0,023.

1. Вывести формулу для периода колебаний физического маятника.

2. Амплитуда гармонических колебаний материальной точки равна 2 см, полная энергия колебаний 3 · 10 -7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила 2,25 · 10 -6 Н?

1. Вывести формулу, связывающую логарифмический декремент и коэффициент затухания.

2. Записать уравнение свободных гармонических колебаний, если известно, что амплитуда колебаний 5 см, период равен 4 с, начальная фаза равна нулю. Найти амплитуду скорости и ускорения. Колебания совершаются по закону синуса.

Ответ: х = 5 sin(pt / 2) см; »7,85 см/с; »12,3 см/с 2

1. Как изменится период затухающих колебаний физического маятника, если закрепить тормозящую пластину выше ее первоначального положения?

2. Материальная точка массой 10 г колеблется по закону x = 5 sin(wt) см. Период колебаний равен 5 с. Найти максимальную силу, действующую на эту материальную точку, и полную энергию колебания.

Ответ: 0,8 мН; 20 мкДж.

1. Как связана частота собственных колебаний с частотой затухающих колебаний?

2. Период свободных гармонических колебаний равен 5 с, начальная фаза p/5. Чему равна фаза колебания в момент времени 4 с?

1. Что называется резонансом? Вывести формулу для резонансной амплитуды.

2.Амплитуда синусоидальных гармонических колебаний 10 см, период 12 с, начальная фаза равна нулю. Найти смещение, скорость и модуль ускорения колеблющегося тела через 3 с после начала колебаний.

Ответ: 10 см; 0; 2,7 см/с 2

1. Вывести формулу для определения резонансной частоты колебаний.

2. Материальная точка совершает гармонические колебания. Максимальная скорость точки 10 см/с, максимальное ускорение 100см/с 2 . Найти циклическую частоту, период колебаний и амплитуду.

Ответ: 10 с –1 ; »0,628 см; 1см.

1.Чему равен сдвиг фаз колебаний физического и математического маятников при резонансе?

2. Уравнений колебаний точки задано в виде x = sinwt, период Т = 12 с. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.

Ответ: 6·n с; 3(2n + 1) c, n = 0,1,2,3 …

1. Какой физический смысл имеет логарифмический декремент затухания?

2. Период собственных колебаний пружинного маятника равен 0,55 с. В вязкой среде период затухающих колебаний этого же маятника стал равным 0,56 с. Определить резонансную частоту n_рез колебаний.

Ответ: 1,75 Гц.

1. Савельев И.В. Курс общей физики в 3т., т.2, т.3 – М.: Наука, 1982

2. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа,1999.

3. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Физматлит, 2001.

4. Волькенштейн В.С. Сборник задач по общему курсу физики. – М.: Наука, 1979.

5. Сборник заданий для индивидуальной самостоятельной работы студентов ФАО и групп очно- заочной формы обучения / Под ред. В.В. Соковишина и Л.В. Спиридоновой МГУПП. – М.: МГУПП, 1997.

6. Лабораторный практикум по механике и молекулярной физике./ Под ред. Л.В. Спиридоновой – М.: МГУПП, 2002.

Лабораторная работа 1. Определение плотности тел правильной геометрической формы . . . . . . . .3

Лабораторная работа 2. Исследование законов поступательного движения

и проверка основного закона динамики . . . . .7

Лабораторная работа 5. Изучение законов вращательного движения на маятнике Обербека . . . . . . . . .12

Лабораторная работа 10. Определение логарифмического декремента затухания и приведенной длины физического маятника . .17

Лабораторные работы №1 и №2 – к.т.н. доцент Спиридонова Л.В.

Лабораторные работы №5 и №10 – к.физ.-мат.н. доцент Соковишин В.В.

Содержание

Вектор силы (Определение, Пример)
ЧТО ТАКОЕ ВЕКТОР СИЛЫ
Опыт по определению вектора силы
Равновесие сил
Равновесие трех сил, треугольник сил
Похожие страницы:
Чему равен вектор силы
Векторная сила
Задача обучения
Основные пункты
Термины
Момент силы
Сила: что это за величина
Плечо силы
Рычаг
Момент силы
Расчет момента силы
Правило моментов
Вектор силы (Определение, Пример)
ЧТО ТАКОЕ ВЕКТОР СИЛЫ
Опыт по определению вектора силы
Равновесие сил
Равновесие трех сил, треугольник сил
Похожие страницы:
💡 Видео

Видео:Построение проекции вектора на осьСкачать

Вектор силы (Определение, Пример)

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

ЧТО ТАКОЕ ВЕКТОР СИЛЫ

Это то, что тянет и толкает; силы мы чувствуем, когда они на нас действуют; силы растягивают пружины, заставляют тело двигаться быстрее. Мы будем измерять силы при помощи пружинных весов. Поскольку эти приборы обычно градуируют в килограммах силы мы будем пока выражать силу тоже в килограммах силы.

При сооружении и проектировании мостов, зданий, кранов, машин инженеров очень заботит сложение сил или же разность сил для определения силы, необходимой для достижения равновесия. Можно показать, что силы — это векторы, т. е. они подчиняются правилу геометрического сложения.

Векторному сложению и разложению уравновешенных сил посвящен раздел физики, называемый «статикой». Это большой, но скучный раздел физики, и большинство учебников уделяет ему много места, излагая приемы решения задач инженерной статики. Мы ограничимся лишь несколькими примерами, и даже их, пожалуй, лучше было бы опустить, чтобы уделить больше времени изучению силы и движения.

Прежде всего мы должны удостовериться в том, что силы — это векторы. Сказать, что они должны быть векторами, поскольку они характеризуются величиной и направлением, недостаточно. Это не убеждает нас в том, что силы складываются геометрически.

Хотя это утверждение кажется вполне правдоподобным, особенно тем, кто имеет дело с канатами и веревками на кораблях или кому приходится заниматься разбивкой палаток, мы же должны проворить его непосредственно.

Опыт по определению вектора силы

Часто прибегают еще к одному способу проверки. Этот способ проще, но его косвенный характер порой (не совсем добросовестно) игнорируют. К узлу прикладывают две тянущие силы F_А и F_В (применяют гири и блоки или пружинные весы), а третья сила F_С удерживает узел в покое. Затем при помощи построения определяется сумма сил F_А и F_В .

Она равна и проти воположна силе F_С. Это требует дополнительного доказательства, поскольку F_С не равнодействующая (сумма) двух других сил, а «равновесная» сила, необходимая, чтобы им противостоять.

Рис. Косвенная проверка векторного сложения сил.

Равновесие сил

Если на какую-нибудь деталь крана или моста действует несколько сил сразу, а инженеру нужно, чтобы она была и оставалась в состоянии покоя, то для этого сумма всех действующих сил должна быть равна нулю. Тогда в соответствии с представлением Галилея эта деталь должна либо постоянно двигаться, либо постоянно оставаться в состоянии покоя.

В этом случае мы говорим, что силы находятся «в равновесии». Если сумма нескольких сил равна нулю, то это должно быть видно на диаграмме векторного сложения; длина линии, соединяющей исходную точку диаграммы с конечной, должна быть равна нулю. Это означает, что векторная диаграмма должна представлять собой замкнутую фигуру.

Таким образом, если сумма сил равна нулю, то конец векторного многоугольника должен прийти обратно к началу. Это иллюстрирует рис. 3. Условие равенства нулю равнодействующей для постоянного равновесия сил должно выполняться для всей конструкции, например для всего крана или моста, но оно должно также выполняться для каждой отдельной детали конструкции, находящейся в состоянии равновесия.

Применяя это условие к какой-нибудь определенной детали, например к стреле крана, к одной опоре моста, к заклепке, связывающей воедино несколько различных деталей моста, или к грузу маятника, нужно быть внимательным и учитывать все силы, действующие на данную деталь. Тогда мы сможем утверждать, что имеем полный набор сил, образующих замкнутую векторную диаграмму, если, конечно, деталь находится в равновесии.

При решении задач не следует включать в рассмотрение силы, приложенные к другим деталям. Сначала выберите и пометьте выбранную деталь, которая, как вы считаете, находится в равновесии.

Равновесие трех сил, треугольник сил

Если три силы находятся в равновесии, то их векторная диаграмма должна представлять собой замкнутый треугольник (рис. 4). Если известны две силы, то можно вычислить величину и направление третьей.

а — три силы в равновесии) б — три силы не находятся в равновесии.

Этим пользуются при решении инженерных задач. Во многих конструкциях на каждую деталь, играющую важную роль, действуют как раз три силы. Чтобы конструкция была устойчивей, каждая деталь должна оставаться в состоянии покоя; сумма всех действующих на нее сил должна быть равна нулю. Таким образом, если к любой детали приложены три силы, мы строим для них замкнутый треугольник.

Чему равен вектор силы

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Векторная сила

Физика > Сила в двух измерениях

Силы действуют в определенном направлении и характеризуются размерами, зависящими от того, насколько сильным был толчок или тяга.

Видео:Физика | Ликбез по векторамСкачать

Задача обучения

Объяснить, почему силы классифицируются как векторные величины.

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Основные пункты

При вычислении результата двух действующих сил, нужно знать величину и направление обоих.
Чтобы определить общую силу от двух действующих, необходимо воспользоваться правилом параллелограмма сложение векторов.
Диаграммы свободного тела выступают удобным способом отслеживания действующих сил.

Видео:Как построить проекцию вектора?Скачать

Термины

Результирующий – вектор, выступающий векторной суммой квадратных векторов.
Диаграмма свободного тела – графическое изображение действующих сил.
Вектор – направленное количество, обладающее величиной и направлением (между двумя точками).

Силы действуют в определенном направлении и обладают размером, зависящем от силы, приложенной к толчку или тяге. Это векторные силы. Чтобы определить результат действия двух сил, нужно знать их величины и направление. Например, два человека тянут за веревку с известной силой, но в неизвестных направлениях. Они могут отображать перетягивание каната или тянуть вместе. Если мы не узнаем, то остается неясным, что делать дальше: суммировать или вычитать.

Диаграммы свободного тела объекта на наклонной плоскости

Когда две силы воздействуют на точечную частичку, то результирующая сила (чистая) определяется правилом параллелограмма сложения векторов: добавление двух векторов, отображенных сторонами параллелограмма, дают эквивалентный результирующий вектор. Его величина зависит от разности величин двух сил.

Можно также использовать диаграммы (график) свободного тела. Их отображают с учетом углов и относительных величин векторов силы.

Видео:Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Момент силы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Вычитание векторов. 9 класс.Скачать

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

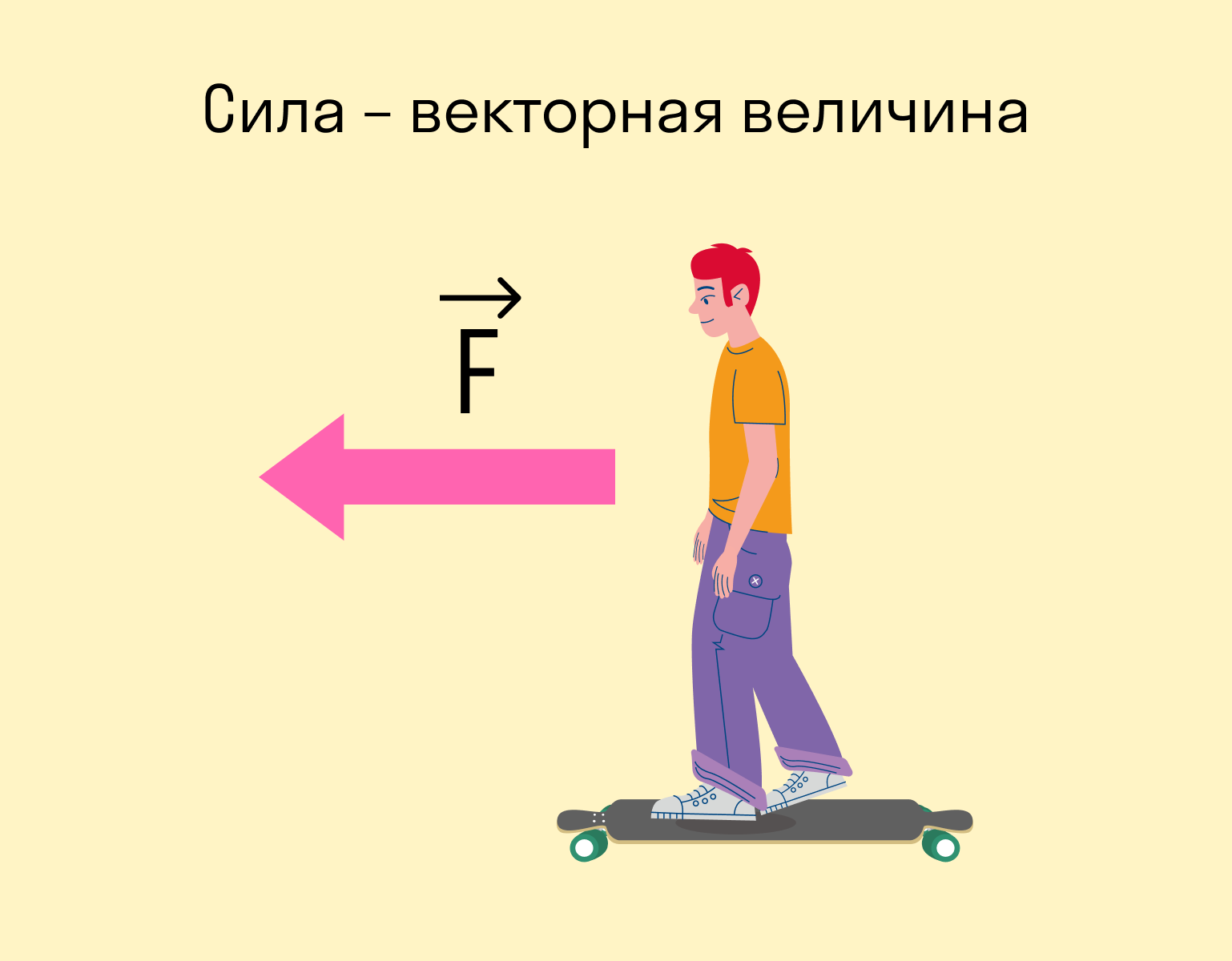
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Видео:Как проецировать вектор сил на оси | ЕГЭ Физика | Николай Ньютон. ТехноскулСкачать

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Видео:Тренировочные задания по теме: "Результирующая сила"Скачать

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы

M = Fl

M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]

Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.

Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.

На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.

То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

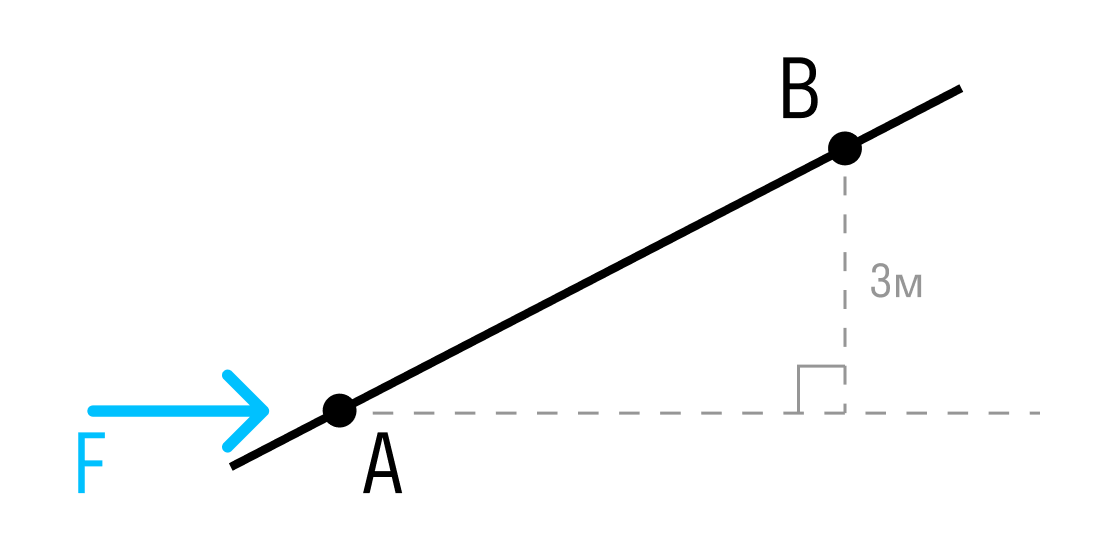
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

Видео:Сложение векторов. 9 класс.Скачать

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов

M1 + M2 +. + Mn = M’1 + M’2 +. + M’n

M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

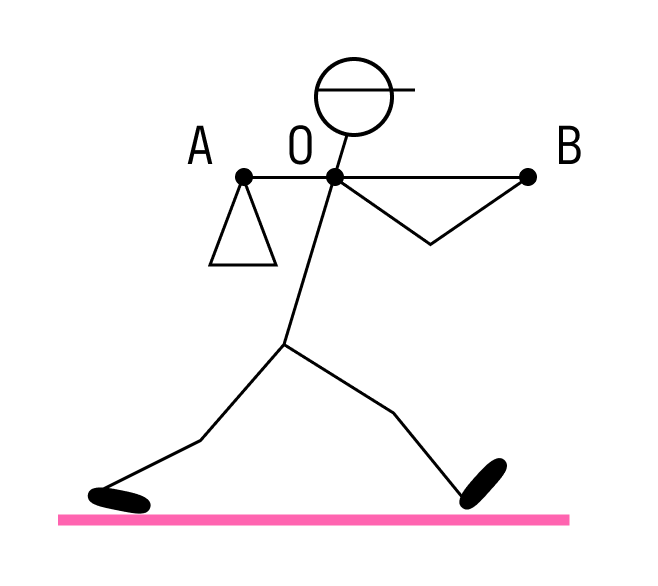
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

Ответ: расстояние ОА равно 30 см

Задача 3

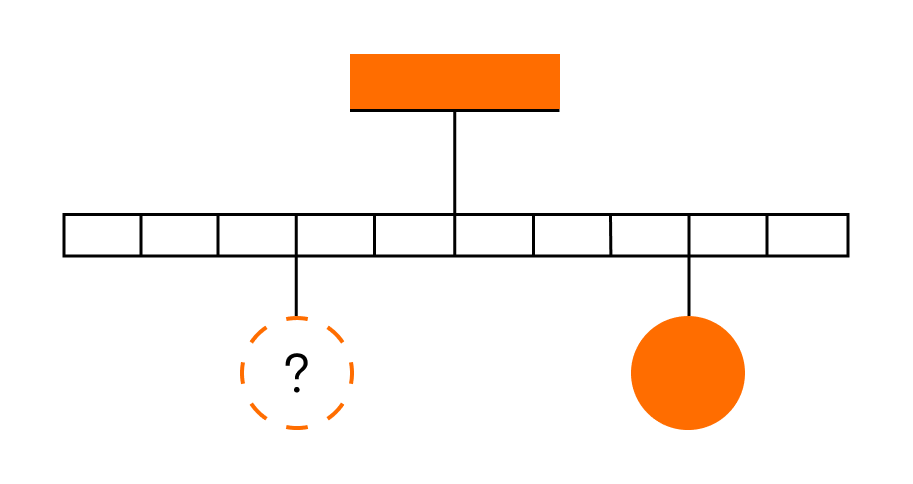
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

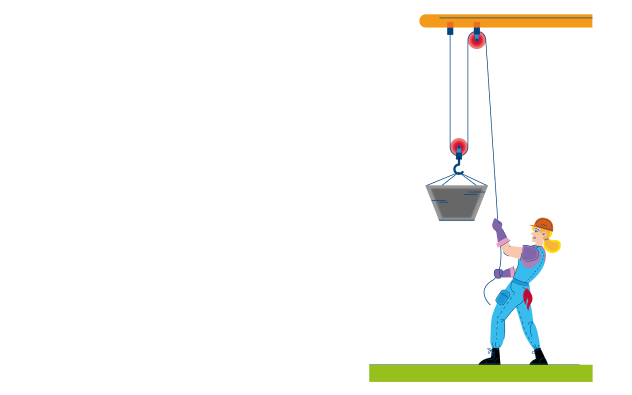
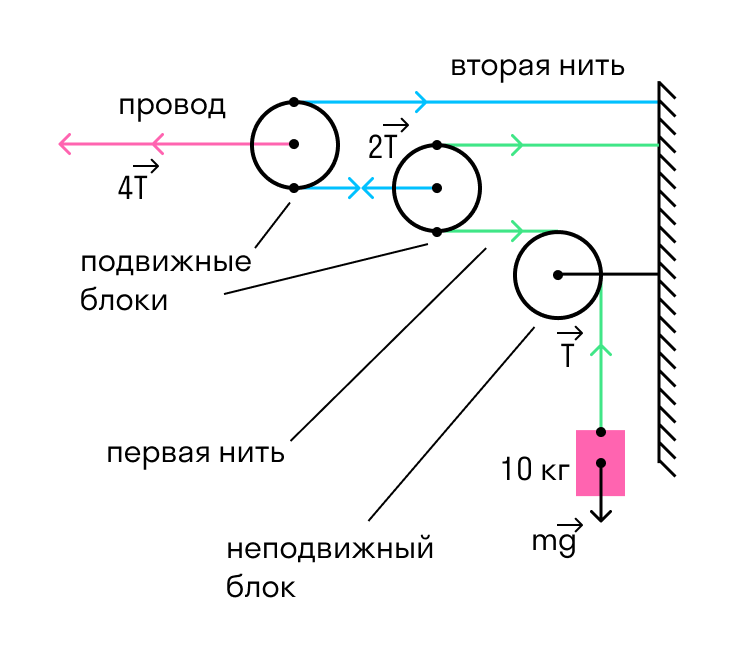
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Вектор силы (Определение, Пример)

Видео:Построение векторной диаграммы. Цепь RLCСкачать