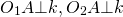Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

We are checking your browser. mathvox.ru
Видео:Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d75ffb8ca3e75af • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Видео:Касание окружностей | Задачи 16-21 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Касание двух окружностей
Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.
Общая точка двух окружностей называется точкой касания окружностей.
Касание окружностей может быть внешним и внутренним.
Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной.
Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.
Касающиеся окружности имеют только одну общую точку — точку касания.
Центры касающихся окружностей и их общая точка касания лежат на одной прямой.
При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания:
По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k.
Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой.
Что и требовалось доказать .
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами окружностей равно разности радиусов:
Видео:ОГЭ Задание 25 Внешнее касание двух окружностейСкачать

Окружность. Относительное взаимоположение окружностей.
Если две окружности имеют только одну общую точку, то говорят, что они касаются.
Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.
Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).
Теорема.
Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.
Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.
Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.
Следствие.
Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.
Теоремы.
1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.
2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.
Признаки различных случаев относительного положения окружностей.
Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.
Эти окружности могут находиться в следующих 5-ти относительных положениях:
1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .
2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.
3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.
4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.
5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,
d R + R1, то окружности расположены одна вне другой, не касаясь.
2. Если d = R + R1, то окружности касаются извне.
3. Если d R — R1, то окружности пересекаются.
4. Если d = R — R1, то окружности касаются изнутри.
5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.
🌟 Видео
Касание окружностейСкачать

Касание окружностей | Задачи 11-15 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Касание окружностей | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Радиус, проведенный в точку касания, перпендикулярен данной касательной. Доказательство. #геометрияСкачать

Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

ЕГЭ Задание 16 Внутреннее касание двух окружностейСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Три окружности касаются прямой и друг друга внешним образомСкачать
Геометрия. 8 класс. Урок 02 Касательные к окружностиСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Теорема о числе точек пересечения двух окружностейСкачать

ЕГЭ Задание 16 Две касающиеся окружностиСкачать
Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

1 2 4 сопряжение окружностейСкачать