- Аннотация научной статьи по физике, автор научной работы — Михляев С. В.
- Похожие темы научных работ по физике , автор научной работы — Михляев С. В.
- Investigation of a non-iterative technique of least squares circle fitting
- Текст научной работы на тему «Исследование неитерационного метода наименьших квадратов для оценивания параметров аппроксимирующей окружности»
- Метод наименьших квадратов
- В чем именно заключается МНК (метод наименьших квадратов)
- Как вывести формулы для вычисления коэффициентов
- Как изобразить МНК на графике функций
- Доказательство метода МНК
- Математика на пальцах: методы наименьших квадратов
- Минимум квадратичной формы
- Уравнение Лапласа с граничным условием Дирихле
- Уравнение Пуассона
- Пример из жизни
- 📹 Видео
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Аннотация научной статьи по физике, автор научной работы — Михляев С. В.
Приведены аналитические выражения для смещений оценок параметров аппроксимирующей окружности, получаемых при использовании неитерационного метода наименьших квадратов. Для компенсации смещений предложена комбинированная схема оценивания по выборкам из различного количества точек.
Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать

Похожие темы научных работ по физике , автор научной работы — Михляев С. В.
Видео:Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Investigation of a non-iterative technique of least squares circle fitting
Analytical expressions for least squares estimation of parameters of the fitted circle and their biases produced by a non-iterative technique are given. To compensate biases, the complex estimation technique utilizing samples of various quantities of approximated points is offered.
Видео:Метод наименьших квадратов. Квадратичная аппроксимацияСкачать

Текст научной работы на тему «Исследование неитерационного метода наименьших квадратов для оценивания параметров аппроксимирующей окружности»
Исследование неитерационного метода наименьших квадратов для оценивания параметров аппроксимирующей окружности
Институт автоматики и электрометрии СО РАН Новосибирск, Россия
Analytical expressions for least squares estimation of parameters of the fitted circle and their biases produced by a non-iterative technique are given. To compensate biases, the complex estimation technique utilizing samples of various quantities of approximated points is offered.
Необходимость оценки параметров окружности, аппроксимирующей данные измерений, возникает в различных задачах, связанных с техническим контролем, обработкой изображений и т.д. 4. В силу нелинейности решаемой при этом оптимизационной задачи, для определения радиуса и координат центра аппроксимирующей окружности, как правило, применяются различные итерационные алгоритмы, основанные, в частности, на методе наименьших квадратов (МНК) и минимизирующие среднеквадратичное отклонение точек от аппроксимирующей окружности 10. Основной недостаток таких алгоритмов — значительные вычислительные затраты, которые не всегда допустимы в практических приложениях. Возможно также использование прямого неитерационного метода оценки параметров окружности (МНК2), являющегося по сути методом наименьших квадратов, примененным не к расстояниям, а к квадратам расстояний между точками [1, 10]. МНК2 позволяет получить решение в аналитическом виде, но дает смещенные оценки параметров [9, 10]. Смещение особенно существенно при аппроксимации фрагмента окружности в виде дуги с небольшим значением центрального угла. Для уменьшения смещения оценок параметров разработаны различные подходы, требующие, однако, дополнительных вычислительных ресурсов [10].
В работе [5] показано, что существенное уменьшение величины смещения оценок в МНК2 (МНК2-оценок) обеспечивается при использовании четырехточечной схемы аппроксимации дуги окружности. Погрешность определения параметров окружности при этом может быть допустимой для различных практических приложений. Результаты работы [5] получены путем численного моделирования в предположении независимости законов распределения погрешностей задания координат аппроксимируемых точек по координатным осям x и у.
В настоящей работе полученные в [5] результаты обобщены на случай независимых распределений погрешностей задания положений аппроксимируемых точек по радиальным и угловым координатам. Приведены аналитические выражения для смещений МНК2-оценок координат центра и радиуса окружности в зависимости от погрешностей
© Институт вычислительных технологий Сибирского отделения Российской академии наук, 2008.
определения координат аппроксимируемых точек (дисперсии шума), их количества, углового распределения вдоль аппроксимирующей дуги, центрального угла дуги. Предложена комбинированная схема оценки параметров, использующая выборки из различного количества аппроксимируемых точек и обеспечивающая получение несмещенных оценок. Теоретические результаты подтверждены численными расчетами.
1. Анализ смещений оценок параметров аппроксимирующей окружности
Критерий оптимизации в рассматриваемом методе МНК2 записывается в следующем виде:
— Хо)2 + (уз- Уо)2 — — хо)2 + (у — Уо)2)) >> (1)
Л = — хо)2 + (у* — уо)2), (2)
где (хг, уг) — координаты исходных точек (г = 1. , N), Л2 — средний квадрат радиуса аппроксимирующей окружности, (хо,уо) — координаты центра окружности. Соотношение (1) имеет аналитическое решение:
Л2 = х2 + у2 — 2(хоХ + уоУ) + Хо + у^, (3)
где черта сверху означает усреднение по выборке из N точек. Координаты центра окружности вычисляются по формулам
Хо = (&1С2 — С1&2)/( , а угловые скобки обозначают усреднение по множеству реализаций при фиксированном значении i.
Величины смещений ДЯ2 и ДЯ для среднего квадрата Я2 и радиуса Я соответственно определяются из выражений (2)-(5) при усреднении по множеству N-точечных выборок:
ДЯ2 = -1 = a2 — 2 + , (7)
где параметр Я в (8) определяется из выражения (3).
Нелинейная зависимость соотношений (4) от Дi не позволяет выполнить усреднение непосредственно в выражениях (7), (8). Для решения этой проблемы воспользуемся разложениями xo и yo в ряды по степеням Д^
A 1 / „ „ „ Bi „ Bi „ B2 „ /Вл2
xo = 2B K 2B^(Ao + Ai — AoB0 + a2 — AiB0 — AoB0 + Ч^) + •••), (9)
У0 = 2B M 2B0(Po + pi — p0f + p2 — piB — p0Bo + Mf )’2 + . . .), (10)
где в соответствии с (4) использованы разложения
A = (biC2 — cib2)/2N2 « Ao + A^) + А2(Д2) + .
В = (ai&2 — b1)/2N2 « Bo + Bi(^) + В2(Д2) + . (11)
P = (bici — aiC2)/2N2 « Po + Pi(^) + Р2(Д2) + • • •
Из выражений (5), (9)-( 11) можно получить следующие результаты для средних значений:
/a2 = cos di/C — 2(1 — 2cos2 9i + cos 9i )(cos3 9i — cos 9i cos2 9^/sin2 9i/C2, (12)
=0, = a2/(CN), = a2/(Nsin2 9i), (13)
= a2/N + cos 9i; = a2/N, (14)
где введено обозначение
C = cos2 9i — cos 9i •
Соответствующее (10) среднее значение = 0 обусловлено выбранной симметричной схемой задания угловых координат исходных точек: sin 9i = 0.
Отметим, что при получении выражений (12)-(14) было использовано соотношение
справедливое для любых зависящих от 9 функций /1(й) и /2(9).
Подставляя (12)—(14) в (7), можно получить требуемое аналитическое выражение для величины смещения оценки среднего квадрата радиуса окружности ДЯ2:
ДЯ2 = a2[1 — 4/N + 1/(NC) + 1 /sin2 0¿/N] — 2cos 9i • (15)
Величина смещения оценки радиуса АЛ (8) может быть получена аналогичным образом, при разложении выражения для радиуса окружности Л = J1 + а в ряд по степеням А*, где
а = 2А + А2 — 2(xoX + yoy) + x0 + y2.
Можно показать, что
АЛ = а2/2[1/2 — 4/N + (1 — cos 0* (2 — cos2 0*))/sin2 0*/С] — cos 0* . (16)
Выражения (12), (15), (16) определяют требуемые аналитические зависимости оцениваемых параметров и их смещений от количества исходных точек, их углового распределения по дуге аппроксимирующей окружности, величины центрального угла дуги и дисперсии шума координат аппроксимируемых точек.
2. Результаты моделирования
Для проверки справедливости полученных аналитических соотношений, исследования статистических характеристик оценок и их зависимостей от вариаций различных параметров проводилось численное моделирование МНК2. При моделировании для получения статистических характеристик использовалось 106 выборок исходных аппроксимируемых точек, координаты которых задавались, в соответствии с соотношениями (5),
с аддитивным нормально распределенным шумом N(0, а2) при нулевом среднем и дис-2
На рис. 1 и 2 представлены расчетные данные, полученные в результате численного моделирования и вычисленные согласно полученным выше аналитическим оценкам, для небольших значений N и Л = 20 мм, а = 0.3 мм. Отметим, что характер изменения приведенных зависимостей при вариациях Л и а близок к представленному нами в работе [5]. Абсолютные значения оцениваемых параметров, использовавшиеся при расчетах, получаются из аналитических оценок для относительных величин путем следующих замен: АЛ ^ ЛАЛ, АЛ2 ^ Л2 А Л2, x0 ^ Лх0, y0 ^ Лу0, а ^ Ла. Поведение показанных на этих рисунках зависимостей при больших значениях N не представляет интереса из-за значительных величин смещений оцениваемых параметров, присущих рассматриваемому методу аппроксимации. Для удобства сравнения оценок (7) и (8) на рис. 2 приведены зависимости для параметра АЛ1 = V — Л.
Из рис. 1 следует, что при 00 + )/2 — Л, где нижние индексы соответствуют четырех- и пятиточечной схеме аппроксимации. Из рис. 3 следует, что комбинированная схема обеспечивает получение практически несмещенных оценок для квадрата радиуса окружности при различных значениях 00. Незначительные для практических приложений отклонения расчетных данных от аналитических оценок для малых значений 00 обусловлены возрастанием дисперсии и погрешностей численных вычислений при уменьшении центрального угла аппроксимирующей дуги 00.
Рис. 1. Зависимости смещения АЯ оценки радиуса окружности от количества аппроксимируемых точек N при различных значениях центрального угла дуги 0о: сплошные линии — аналитические оценки, символы — результаты моделирования
Рис. 2. Зависимости параметра АЯ1 = у/ -Я от количества аппроксимируемых точек N при различных значениях центрального угла дуги сплошные линии — аналитические оценки, символы — результаты моделирования
Рис. 3. Зависимости смещения AR45 при комбинированной схеме оценки радиуса окружности от центрального угла дуги во: сплошная линия — аналитические оценки, символы — результаты моделирования
Расчеты показывают, что введение дополнительного шума в угловое распределение точек со среднеквадратичным отклонением (СКО) в несколько градусов слабо сказывается на полученных результатах.
При выводе выражений для оценок параметров предполагалось симметричное относительно оси x расположение аппроксимируемых точек, при этом не накладывалось никаких ограничений на угловые координаты точек. Полученные соотношения поэтому могут быть использованы для исследования зависимости оцениваемых параметров от вариаций углового положения точек. Наиболее интересными представляются случаи с малым количеством аппроксимируемых точек N = 4 и N = 5, обеспечивающими достаточно малое смещение параметров при значениях в0 20°. Для N = 5 смещение оценки радиуса при ^ > 20° прак-
Рис. 4. Зависимости смещения АЯ и СКО-оценки радиуса окружности от углового отклонения р внутренних аппроксимируемых точек от крайних при N = 4, N = 5 и во = 90°: символы — результаты моделирования; сплошные и штриховые линии для АЯ — аналитические оценки
Рис. 5. Зависимости смещения АЯ45 при комбинированной схеме оценки радиуса окружности от углового отклонения р внутренних аппроксимируемых точек от крайних при одинаковых значениях р для N = 4 и N = 5: сплошная линия — аналитические оценки, символы — результаты моделирования
тически постоянно и по абсолютной величине существенно превосходит аналогичный показатель для N = 4.
Зависимости смещения ДЯ45 от р показаны на рис. 5. Отметим, что на этом рисунке, в отличие от рис. 3, угловые положения внутренних точек для N = 4 и N = 5 одинаковы, и аппроксимируемые выборки точек для различных N отличаются лишь центральной точкой при в = 0. Для во = 90° минимальное смещение достигается в окрестности значения р = 30°, соответствующего равномерному угловому распределению точек при N = 4.
Расчеты показывают, что наличие шумовой составляющей в несколько градусов в угловом положении точек слабо влияет на характер представленных на рис. 4 и 5 зависимостей. Значительные изменения имеют место лишь для N = 4 при близком расположении внутренних и крайних точек, соответствующем малым значениям
Несмещенные оценки ДЯ45 в комбинированной схеме могут быть получены для различных сочетаний значений углов р = и р = соответствующих N = 4 и N = 5, что поясняется рис. 6. На этом рисунке показаны зависимости и от р для N = 4 и N = 5, из которых следует, что компенсация смещения оценки достигается для любой пары значений углов соответствующих одинаковым значениям ДЯ; = = из заштрихованной области. В частности, значению ДЯ; = 0.8 соответствуют два угла = 34.7° и = 17.4°. Заметим, что при одина-
Рис. 6. Зависимости смещений и при комбинированной схеме оценки радиуса окружности от углового отклонения р внутренних аппроксимируемых точек от крайних для N = 4 и N = 5: сплошные линии — аналитические оценки, символы — результаты моделирования
ковом угловом расположении внутренних точек р = р5 = 17.4°, как следует из рис. 5, смещение ДЯ45 существенно превосходит нулевое значение и составляет около 0.02 мм.
Приведенные выше результаты соответствуют независимому распределению шума координат аппроксимируемых точек по Я и 0, что подтверждает общие закономерности, полученные нами ранее для независимого закона распределения шума по х- и у-координатам [5]. Выводы относительно величин смещений оценок параметров окружности, обеспечиваемые для малых значений N при МНК2-аппроксимации, остаются справедливыми и в случае зависимости дисперсии шума по координатам х и у, отличной от (6). Интерес представляют, в частности, задачи, связанные с обработкой изображений и измерением координат точек границ объектов (контуров) вдоль скан-линий, соответствующих анализируемым сечениям изображения х = хс или у = ус. Расчеты показывают, что, в предположении пропорциональной зависимости дисперсии измеряемой координаты границы от ширины контура изображения в анализируемом сечении, величины смещений и дисперсии МНК2-оценок для малых N существенно возрастают лишь с приближением скан-линий к положениям касательных к границе.
Полученные аналитические оценки хорошо совпадают с результатами численного моделирования и подтверждают сделанные нами ранее выводы об эффективности применения неитерационного МНК-оценивания и четырехточечной схемы аппроксимации для оценки радиуса и координат центра аппроксимирующей окружности [5]. Метод аппроксимации МНК2 при N = 4 обеспечивает минимальные смещения оценок, близкие к нулевым значениям, и может применяться в условиях ограниченных вычислительных ресурсов для аппроксимации дуги окружности. Справедливость данного положения подтверждается результатами численного моделирования различных практически важных координатных зависимостей дисперсии шума координат аппроксимируемых точек.
Приведенные в работе аналитические оценки могут использоваться для исследования зависимости оцениваемых параметров от углового положения точек и оптимизации схемы аппроксимации.
Предложенная комбинированная схема аппроксимации по выборкам из различного количества исходных точек позволяет получать несмещенные оценки среднего квадрата радиуса окружности и может применяться в различных прикладных задачах для оценки как радиуса, так и площади круга, ограниченного аппроксимирующей окружностью. В частности, применение такой схемы в системах технического зрения, используемых при автоматическом выращивании кристаллов, позволяет оперативно контролировать площадь кристалла в процессе выращивания, что необходимо для реализации алгоритмов автоматического регулирования и получения кристаллов с заданной геометрией.
Автор выражает признательность В.П. Косых за полезные дискуссии.
[1] Баранов В.Г., Ильясов Н.Ю., Котляр Р.В. и др. Бесконтактное измерение радиуса кривизны сферических поверхностей // Распознавание образов и анализ изображений: новые информационные технологии (РОАИ-5-2000). Тр. Междунар. конф. Самара, 2000. Т. 3. С. 458-462.
[2] Гривов М.Г., ХАЧУМОВ В.М. Определение геометрических параметров объектов по растровым изображениям // Автометрия. 2001. № 1. С. 40-49.
[3] Demeyere M., Dereine E., Eugene C., Naydenoy V. Measurement of cylindrical objects through laser telemetry: application to a new forest caliper // IEEE Trans. Instrument. Measur. 2002. Vol. 51, N. 4. P. 645-649.
[4] Mikhlyaey S.V. Method for measuring the diameter of a growing crystal // Pattern Recogn. Image Analysis. 2005. Vol. 15, N. 4. P. 690-693.
[5] МихляЕВ С.В. Аппроксимация окружности при измерении диаметра кристалла // Вы-числ. технологии. 2007. Т. 12, № 1. С. 61-71.
[6] Zhang Z. Parameter estimation techniques: a tutorial with application to conic fitting // Image Vision Comput. 1997. Vol. 15, N. 1. P. 59-76.
[7] Marquardt D. An Algorithm for least squares estimation of nonlinear parameters // SIAM J. Appl. Math. 1963. Vol. 11. P. 431-441.
[8] Landau U.M. Estimation of a circular arc center and its radius // Comput. Vision, Graphics Image Proces. 1987. Vol. 38. P. 317-326.
[9] Spath H. Least-squares fitting by circles // Comput. 1996. Vol. 57, N. 2. P. 179-185.
[10] Chernov N., Lesort C. Least squares fitting of circles //J. Math. Imaging Vision. 2005. Vol. 23. P. 239-251.
Видео:Метод наименьших квадратов. ТемаСкачать

Метод наименьших квадратов
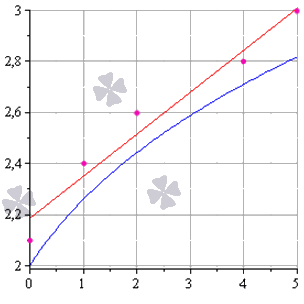
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Видео:Метод наименьших квадратов (МНК)Скачать
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
Видео:Метод наименьших квадратовСкачать

Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Видео:ЦОС Python #1: Метод наименьших квадратовСкачать

Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Видео:Метод наименьших квадратовСкачать

Математика на пальцах: методы наименьших квадратов
Я математик-программист. Самый большой скачок в своей карьере я совершил, когда научился говорить:«Я ничего не понимаю!» Сейчас мне не стыдно сказать светилу науки, что мне читает лекцию, что я не понимаю, о чём оно, светило, мне говорит. И это очень сложно. Да, признаться в своём неведении сложно и стыдно. Кому понравится признаваться в том, что он не знает азов чего-то-там. В силу своей профессии я должен присутствовать на большом количестве презентаций и лекций, где, признаюсь, в подавляющем большинстве случаев мне хочется спать, потому что я ничего не понимаю. А не понимаю я потому, что огромная проблема текущей ситуации в науке кроется в математике. Она предполагает, что все слушатели знакомы с абсолютно всеми областями математики (что абсурдно). Признаться в том, что вы не знаете, что такое производная (о том, что это — чуть позже) — стыдно.
Но я научился говорить, что я не знаю, что такое умножение. Да, я не знаю, что такое подалгебра над алгеброй Ли. Да, я не знаю, зачем нужны в жизни квадратные уравнения. К слову, если вы уверены, что вы знаете, то нам есть над чем поговорить! Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
Знаете ли вы, что такое производная? Вероятнее всего вы мне скажете про предел разностного отношения. На первом курсе матмеха СПбГУ Виктор Петрович Хавин мне определил производную как коэффициент первого члена ряда Тейлора функции в точке (это была отдельная гимнастика, чтобы определить ряд Тейлора без производных). Я долго смеялся над таким определением, покуда в итоге не понял, о чём оно. Производная не что иное, как просто мера того, насколько функция, которую мы дифференцируем, похожа на функцию y=x, y=x^2, y=x^3.
Я сейчас имею честь читать лекции студентам, которые боятся математики. Если вы боитесь математики — нам с вами по пути. Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написан. Я утверждаю, что нет ни одной области математики, о которой нельзя говорить «на пальцах», не теряя при этом точности.
Задача на ближайшее время: я поручил своим студентам понять, что такое линейно-квадратичный регулятор. Не постесняйтесь, потратьте три минуты своей жизни, сходите по ссылке. Если вы ничего не поняли, то нам с вами по пути. Я (профессиональный математик-программист) тоже ничего не понял. И я уверяю, в этом можно разобраться «на пальцах». На данный момент я не знаю, что это такое, но я уверяю, что мы сумеем разобраться.
Итак, первая лекция, которую я собираюсь прочитать своим студентам после того, как они в ужасе прибегут ко мне со словами, что линейно-квадратичный регулятор — это страшная бяка, которую никогда в жизни не осилить, это методы наименьших квадратов. Умеете ли вы решать линейные уравнения? Если вы читаете этот текст, то скорее всего нет.
Итак, даны две точки (x0, y0), (x1, y1), например, (1,1) и (3,2), задача найти уравнение прямой, проходящей через эти две точки:
Эта прямая должна иметь уравнение типа следующего:
Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:
Можно записать это уравнение в матричном виде:
Тут следует сделать лирическое отступление: что такое матрица? Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит. Это зависит от нас, как именно интерпретировать некую матрицу. Периодически я буду её интерпретировать как линейное отображение, периодически как квадратичную форму, а ещё иногда просто как набор векторов. Это всё будет уточнено в контексте.
Давайте заменим конкретные матрицы на их символьное представление:
Тогда (alpha, beta) может быть легко найдено:
Более конкретно для наших предыдущих данных:
Что ведёт к следующему уравнению прямой, проходящей через точки (1,1) и (3,2):
Окей, тут всё понятно. А давайте найдём уравнение прямой, проходящей через три точки: (x0,y0), (x1,y1) и (x2,y2):
Ой-ой-ой, а ведь у нас три уравнения на две неизвестных! Стандартный математик скажет, что решения не существует. А что скажет программист? А он для начала перепишет предыдующую систему уравнений в следующем виде:
И дальше постарается найти решение, которое меньше всего отклонится от заданных равенств. Давайте назовём вектор (x0,x1,x2) вектором i, (1,1,1) вектором j, а (y0,y1,y2) вектором b:
В нашем случае векторы i,j,b трёхмерны, следовательно, (в общем случае) решения этой системы не существует. Любой вектор (alpha*i + beta*j) лежит в плоскости, натянутой на векторы (i, j). Если b не принадлежит этой плоскости, то решения не существует (равенства в уравнении не достичь). Что делать? Давайте искать компромисс. Давайте обозначим через e(alpha, beta) насколько именно мы не достигли равенства:
И будем стараться минимизировать эту ошибку:
Очевидно, что ошибка минимизируется, когда вектор e ортогонален плоскости, натянутой на векторы i и j.
Иными словами: мы ищем такую прямую, что сумма квадратов длин расстояний от всех точек до этой прямой минимальна:
UPDATE: тут у меня косяк, расстояние до прямой должно измеряться по вертикали, а не ортогональной проекцией. Вот этот комментатор прав.
Совсеми иными словами (осторожно, плохо формализовано, но на пальцах должно быть ясно): мы берём все возможные прямые между всеми парами точек и ищем среднюю прямую между всеми:
Иное объяснение на пальцах: мы прикрепляем пружинку между всеми точками данных (тут у нас три) и прямой, что мы ищем, и прямая равновесного состояния есть именно то, что мы ищем.
Видео:Численные методы: Метод наименьших квадратовСкачать

Минимум квадратичной формы
Итак, имея данный вектор b и плоскость, натянутую на столбцы-векторы матрицы A (в данном случае (x0,x1,x2) и (1,1,1)), мы ищем вектор e с минимум квадрата длины. Очевидно, что минимум достижим только для вектора e, ортогонального плоскости, натянутой на столбцы-векторы матрицы A:
Иначе говоря, мы ищем такой вектор x=(alpha, beta), что:
Напоминаю, что этот вектор x=(alpha, beta) является минимумом квадратичной функции ||e(alpha, beta)||^2:
Тут нелишним будет вспомнить, что матрицу можно интерпретирвать в том числе как и квадратичную форму, например, единичная матрица ((1,0),(0,1)) может быть интерпретирована как функция x^2 + y^2:
Вся эта гимнастика известна под именем линейной регрессии.
Видео:11 1 Метод наименьших квадратов ВведениеСкачать

Уравнение Лапласа с граничным условием Дирихле
Теперь простейшая реальная задача: имеется некая триангулированная поверхность, необходимо её сгладить. Например, давайте загрузим модель моего лица:
Изначальный коммит доступен здесь. Для минимизации внешних зависимостей я взял код своего софтверного рендерера, уже подробно описанного на хабре. Для решения линейной системы я пользуюсь OpenNL, это отличный солвер, который, правда, очень сложно установить: нужно скопировать два файла (.h+.c) в папку с вашим проектом. Всё сглаживание делается следующим кодом:
X, Y и Z координаты отделимы, я их сглаживаю по отдельности. То есть, я решаю три системы линейных уравнений, каждое имеет количество переменных равным количеству вершин в моей модели. Первые n строк матрицы A имеют только одну единицу на строку, а первые n строк вектора b имеют оригинальные координаты модели. То есть, я привязываю по пружинке между новым положением вершины и старым положением вершины — новые не должны слишком далеко уходить от старых.
Все последующие строки матрицы A (faces.size()*3 = количеству рёбер всех треугольников в сетке) имеют одно вхождение 1 и одно вхождение -1, причём вектор b имеет нулевые компоненты напротив. Это значит, я вешаю пружинку на каждое ребро нашей треугольной сетки: все рёбра стараются получить одну и ту же вершину в качестве отправной и финальной точки.
Ещё раз: переменными являются все вершины, причём они не могут далеко отходить от изначального положения, но при этом стараются стать похожими друг на друга.
Всё бы было хорошо, модель действительно сглажена, но она отошла от своего изначального края. Давайте чуть-чуть изменим код:
В нашей матрице A я для вершин, что находятся на краю, добавляю не строку из разряда v_i = verts[i][d], а 1000*v_i = 1000*verts[i][d]. Что это меняет? А меняет это нашу квадратичную форму ошибки. Теперь единичное отклонение от вершины на краю будет стоить не одну единицу, как раньше, а 1000*1000 единиц. То есть, мы повесили более сильную пружинку на крайние вершины, решение предпочтёт сильнее растянуть другие. Вот результат:
Давайте вдвое усилим пружинки между вершинами:
Логично, что поверхность стала более гладкой:
А теперь ещё в сто раз сильнее:
Что это? Представьте, что мы обмакнули проволочное кольцо в мыльную воду. В итоге образовавшаяся мыльная плёнка будет стараться иметь наименьшую кривизну, насколько это возможно, касаясь-таки границы — нашего проволочного кольца. Именно это мы и получили, зафиксировав границу и попросив получить гладкую поверхность внутри. Поздравляю вас, мы только что решили уравнение Лапласа с граничными условиями Дирихле. Круто звучит? А на деле всего-навсего одну систему линейных уравнений решить.
Видео:Метод Наименьших Квадратов (МНК)Скачать

Уравнение Пуассона
Давайте ещё крутое имя вспомним.
Предположим, что у меня есть такая картинка:
Всем хороша, только стул мне не нравится.
Разрежу картинку пополам: 
И выделю руками стул:
Затем всё, что белое в маске, притяну к левой части картинки, а заодно по всей картинке скажу, что разница между двумя соседними пикселями должна равняться разнице между двумя соседними пикселями правой картинки:
Код и картинки доступны здесь.
Видео:Метод наименьших квадратовСкачать

Пример из жизни
Я специально не стал делать вылизанные результаты, т.к. мне хотелось всего-навсего показать, как именно можно применять методы наименьших квадратов, это обучающий код. Давайте я теперь дам пример из жизни:
У меня есть некоторое количество фотографий образцов ткани типа вот такой:
Моя задача сделать бесшовные текстуры из фотографий вот такого качества. Для начала я (автоматически) ищу повторяющийся паттерн:
Если я вырежу прямо вот этот четырёхугольник, то из-за искажений у меня края не сойдутся, вот пример четыре раза повторённого паттерна:
Вот фрагмент, где чётко видно шов:
Поэтому я вырезать буду не по ровной линии, вот линия разреза:
А вот повторённый четыре раза паттерн:
И его фрагмент, чтобы было виднее:
Уже лучше, рез шёл не по прямой линии, обойдя всякие завитушки, но всё же шов виден из-за неравномерности освещения на оригинальной фотографии. Вот тут-то и приходит на помощь метод наименьших квадратов для уравнения Пуассона. Вот конечный результат после выравнивания освещения:
Текстура получилась отлично бесшовной, и всё это автоматически из фотографии весьма посредственного качества. Не бойтесь математики, ищите простые объяснения, и будет вам инженерное счастье.
📹 Видео
Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

аппроксимация точек окружностьюСкачать

Метод наименьших квадратов. Регрессионный анализ.Скачать

Метод наименьших квадратов, урок 2/2. Квадратичная функцияСкачать

Математика это не ИсламСкачать

Аппроксимация точек 3d окружностьюСкачать