Медиана делит площадь треугольника пополам
Два треугольника называются равновеликими. Если они имеют одинаковую площадь.
Теорема 1. Медиана делит треугольник на два равновеликих треугольника.
Пусть ВМ – медиана треугольника АВС. Докажем, что

Проведем высоту BH треугольника АВС. Тогда


Так как ВМ – медиана треугольника АВС, то АМ=МС, поэтому



Что и требовалось доказать.
Теорема 2. Медианы треугольника разбивают его на шесть равновеликих треугольников.
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Из теоремы, в частности следует, что если точку пересечения медиан треугольника соединить со всеми его вершинами, то треугольник разобьется на три равновеликие части.
Задача 1 Две медианы треугольника взаимно перпендикулярны и равны соответственно 3 и 4. Найти площадь треугольника.
Пусть в треугольнике АВС медианы АМ и ВЕ равны 3 и 4 соответственно, 


Так как треугольник АВК прямоугольный с прямым углом ВКА, то 
Так как медиан делят треугольник на 6 равновеликих частей, то 
Задача 2 Медианы треугольника равны 6, 8 и 10, найти площадь треугольника.
Пусть медианы АM, BE и CD данного треугольника соответственно равны 6, 8 и 10, К – точка их пересечения. Отложим на продолжении луча ВЕ за точку Е отрезок EF=KE. Соединим точки С, F и A.
Рассмотрим треугольник KAF.

то

Далее, 

Так как 


Вычислим площадь треугольника AKF:

Теперь сравним площади треугольников AKF и АВС: так как AE – медиана треугольника AKF, то




Отметим, что задачу можно решить по-другому, если воспользоваться тем фактом, что:
площадь треугольника, образованного медианами данного треугольника составляет 
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Вопросы для самопроверки:
1. Какие треугольники называются равновеликими?
2. Площадь треугольника равна S. Чему равна площадь каждого из треугольников, на которые его разбивает медиана, проведенная к какой-либо стороне этого треугольника?
3. На сколько равновеликих частей разбивают треугольник проведенные в нем три медианы?
4. Площадь треугольника равна S. Цент тяжести этого треугольника соединили с его вершинами. Чему равна площадь каждого из получившихся треугольников?
5. Площадь треугольника равна 48, чему равна площадь треугольника, составленного из медиан этого треугольника?
6. Площадь треугольника, составленного из медиан некоторого треугольника равна 24, чему равна площадь треугольника?
Задачи для самостоятельного решения:
1. Две медианы треугольника взаимно перпендикулярны и равны соответственно 6 и 8. Найти площадь треугольника.
2. Медианы треугольника равны 3, 4 и 5 найти площадь треугольника.
3. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС.
4. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей, равна 5. Найдите площадь треугольника.
Видео:Найдите площадь треугольника, если его медианы равны 3, 4 и 5Скачать
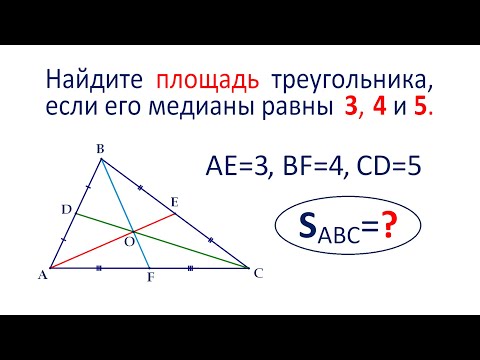
Медиана и площадь треугольника
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` — углы треугольника`ABC`; `a`, `b` и `c` — противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` — высоты к этим сторонам; `r` — радиус вписанной окружности;`R` — радиус описанной окружности; `2p=(a+b+c)` — периметр треугольника; `S` — площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` — формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь — найти косинус, например, угла `M`. По теореме косинусов
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.^$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
$$ 2.^$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
$$ 2.^$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC
DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` — точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` — середина стороны `BC` (рис. 7б), по утверждению $$ 2.^$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.^$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.^$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL«||«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«||«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«||«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` — точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` — площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
| `S_(m_am_bm_c)=3/4S_(abc)`. |
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` — середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
| `x=(2ab)/(a+b)cos varphi/2`. |
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` — точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
Видео:Найдите площадь треугольника, если его медианы равны 12, 15 и 21.Скачать

Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна S
Пусть АМ, ВК, СN – медианы треугольника АВС, О – точка их пересечения.
Площадь треугольника АВО в 3 раза меньше площади треугольника АВС (высота треугольника АВО в 3 раза меньше высоты треугольника АВС).
Тогда площадь треугольника АNO равна площади треугольника АВС (медианы треугольника делят его на 6 равновеликих, то есть равных по площади, треугольников).

Мы получили, что
Построим треугольник DЕF, стороны которого равны медианам треугольника АВС.
EF = АМ, DF = ВК и DE = СN. В этом треугольнике угол DEF равен , и его площадь
Видео:Задача найти площади треугольников при пересечении медианСкачать

Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
🎬 Видео
8. Медиана треугольника и её свойства.Скачать

Медианы и площадь треугольника.Скачать

Все свойства медианы в одной задаче.Скачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Медианы делят треугольник на меньшие треугольникиСкачать
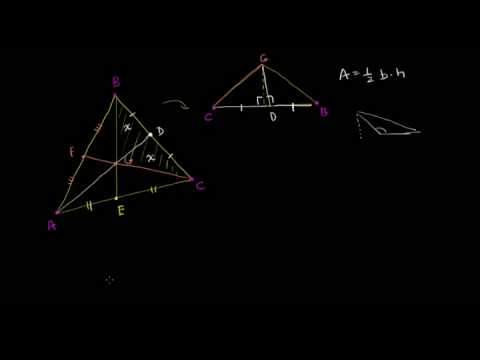
Длина медианы треугольникаСкачать

Все факты о медиане треугольника для ЕГЭСкачать

Площадь треугольника по трем медианам!Скачать

Свойство медианы в прямоугольном треугольнике #shortsСкачать
В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать

Задание 24 Треугольник Медианы Площадь Метаморфозы чертежаСкачать
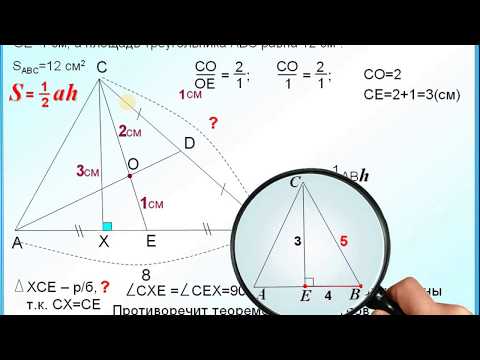
Медиана делит треугольник на два равновеликих. ДоказательствоСкачать

Формулы равностороннего треугольника #shortsСкачать

Найти площадь треугольника если известны сдве его стороны и медианаСкачать
ВЫСОТА ТРЕУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать










