Продолжение сторон ав и сд четырехугольника авсд

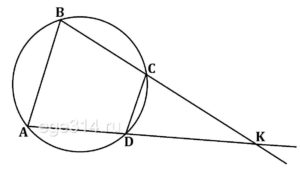
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.

Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.

Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Продолжения сторон AB и CD вписанного четырёхугольника ABCD пересекаются в точке P, а продолжения BC и AD — в точке Q. Докажите, что точки пересечения биссектрис углов AQB и BPC со сторонами четырёхугольника являются вершинами ромба.

Пусть P₁ и P₂ — точки пересечения биссектрисы угла BPC с окружностью, описанной около четырёхугольника ABCD, а Q₁ и Q₂ — биссектрисы угла AQB, причём точка P₁ лежит между P и P₂, Q₁ — между Q и Q₂. Тогда

AP₂ — BP₁ = DP₂ — CP₁, DQ₂ — AQ₁ = CQ₂ — BQ₁,

AP₂ + CP₁ = DP₂ + BP₁, AQ₁ + CQ₂ = DQ₂ + BQ₁.

Сложив почленно эти два равенства, получим, что

AP₂ + AQ₁ + CP₁ + CQ₂ = DP₂ + DQ₂ + BP₁ + BQ₁ = 180 o .

Если K — точка пересечения указанных биссектрис, то

PKQ = P₁KQ₁ = ( AP₂ + AQ₁ + CP₁ + CQ₂) = 90 o .

Если M и N — точки пересечения прямой Q₁Q₂ со сторонами AB и CD, то треугольник PMN — равнобедренный, т.к. его биссектриса PK является высотой. Поэтому MK = KN. Аналогично докажем, что K — середина второй диагонали полученного четырёхугольника. Следовательно, это ромб.

Видео:Геометрия Известно, что около четырехугольника ABCD можно описать окружность и что продолжениеСкачать

Решение №1222 Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС …

Известно, что около четырехугольника АВСD можно описать окружность и что продолжения сторон АD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники КАВ и КСD подобны.

Источник: ОГЭ Ященко 2021 (36 вар)

В ΔКАВ и ΔКСD ∠К общий.
Четырёхугольник АВСD вписан в окружность сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180º
∠ABC = 180º – ∠ADC

∠ADC и ∠СDK смежные их сумма равна 180º:

∠ADC + ∠СDK = 180º
∠СDK = 180º – ∠ADC

Из этих двух равенств получаем:

∠ABC = ∠СDK

Тогда ΔКАВ и ΔКСD подобны по двум равным углам.
Что и требовалось доказать.

📸 Видео

№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

Геометрия Продолжение боковых сторон AB и CD в трапеции ABCD пересекаются в точке E. НайдитеСкачать

Геометрия Стороны AB и CD выпуклого четырехугольника ABCD равны. Через середины диагоналей AC и BDСкачать

[ОГЭ] Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120Скачать

ОГЭ по математике. Задача 25-2Скачать

ОГЭ по математике. Задание 15Скачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

В трапеции ABCD AB=CD, ∠BDA=35° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

2128 в четырёхугольник ABCD вписана окружность AB = 7 BC = 12 CD = 9Скачать

В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать

Задание 24 из Варианта Ларина №229 обычная версия ОГЭ-2020.Скачать

В трапеции ABCD AB=CD, AC=AD и ∠ABC=95° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Геометрия Продолжение боковых сторон AB и CD трапеции ABCD пересекаются в точке M. Найдите AM, еслиСкачать

Геометрия Боковые стороны AB и CD трапеции ABCD равны соответственно 28 и 35, а основание BC равно 7Скачать

ОГЭ по математике, задание 26, тренировочный вариант 1Скачать

🔴 В трапеции ABCD известно, что AB=CD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

В четырёхугольник ABCD вписана окружность. AB = 23 ,BC = 9 ,CD = 13 .Найдите четвертую сторонуСкачать