Векторы зачем они нам (7 видео) | Курс школьной геометрии

Вектор

В математике и физике, вектор является величиной, которая характеризуется своим направлением, а также численным значением. Когда же используются векторы и зачем они нужны? Векторы используют для записи тех величин, которые обыкновенными числами записать невозможно. Допустим, нам необходимо описать положение предмета относительно некоторой точки. Разумеется, мы можем вычислить расстояние между точкой и предметов и записать его обыкновенным числом, но это не будет полной характеристикой. А вот если мы запишем данную величину вектором, то помимо расстояния, мы будем еще знать направление, в котором данный предмет находится относительно заданной точки.

Графически все векторы изображаются, как направленные отрезки определенной заданной длины.

Что же такое свободные векторы? По-другому свободные векторы можно еще назвать и равными. Это такие векторы, у которых совпадает, как модульная величина (то есть отрезок по значению одинаковый), так и направление.

А теперь поговорим не много о действиях над векторами. Зачем вообще придумали слаживать вектора? На самом-то деле, просто решили, что можно вывести один вектор, который бы оказывал тоже воздействие, что и два других вектора. Как вы догадались, два других вектора, это наши слагаемые, а один вектор, который оказывает такое же воздействие – это наша сумма. Вектора складываются несколькими способами, в математики они называются «правилами». Первый – «правило треугольника», второй – «правило «параллелограмма». Стоит отметить и то, что мы можем сложить и три, и четыре , и пять векторов, но делать это надо постепенно, то есть попарно.

Содержание

Знакомимся с вектором
Линейная алгебра
Что такое вектор
Как записывать
Скаляр
Как изображать
И зачем нам это всё
Что дальше
Проектная работа. Вектор. 9 класс
Почти одновременно с ним исследованиями в том же направлении занимался английский математик — Уильям Кингдон Клиффорд (1845–1879)
📽️ Видео

Видео:Что такое векторы?Скачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Векторы в математикеСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Что такое вектор

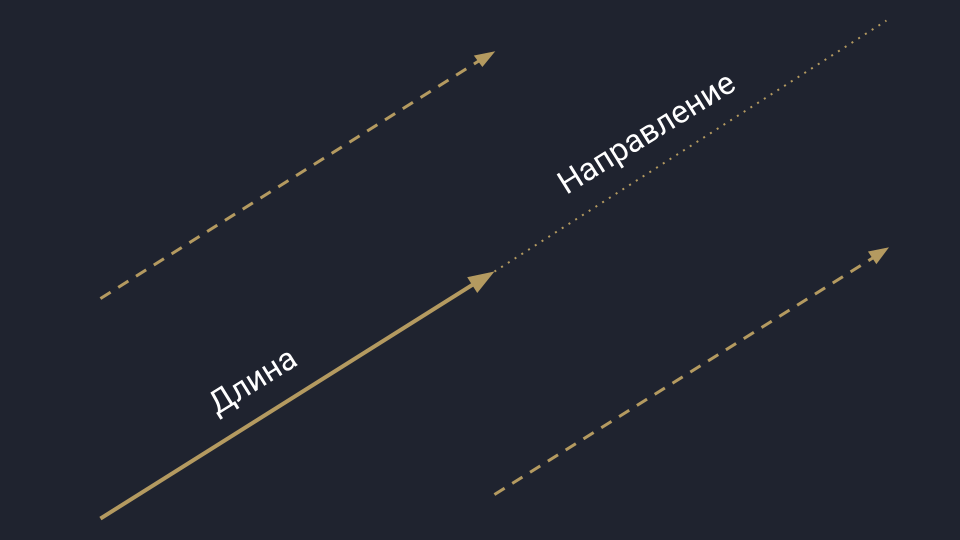
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

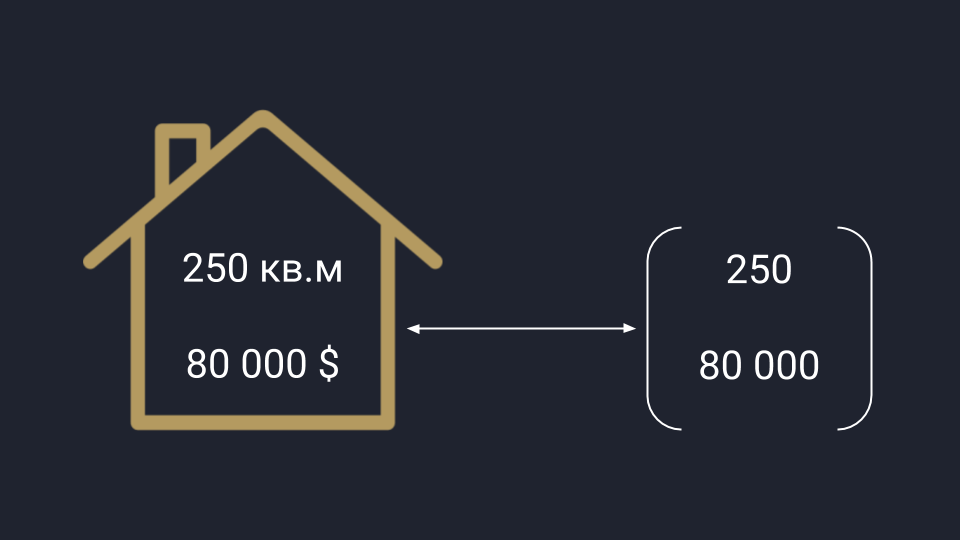
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

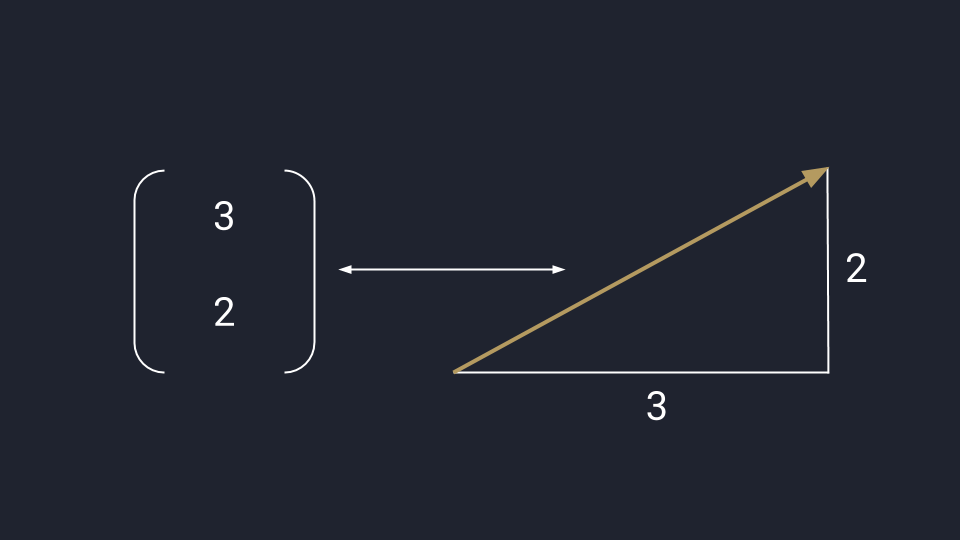
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

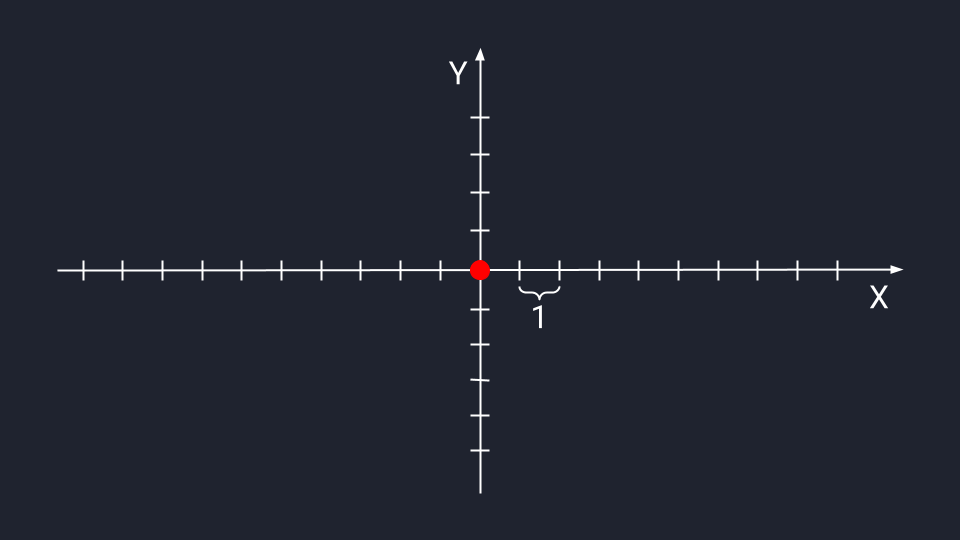
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:Действия с векторамиСкачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

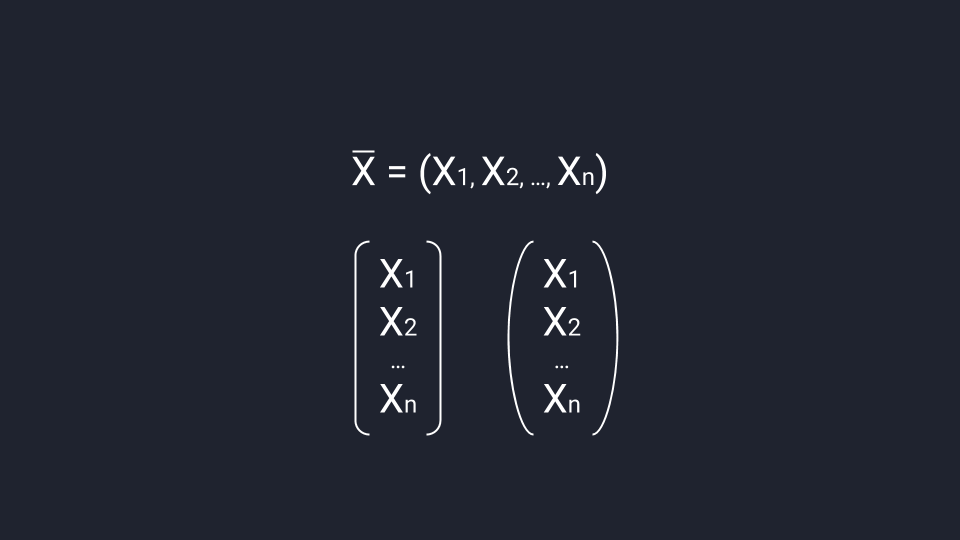
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

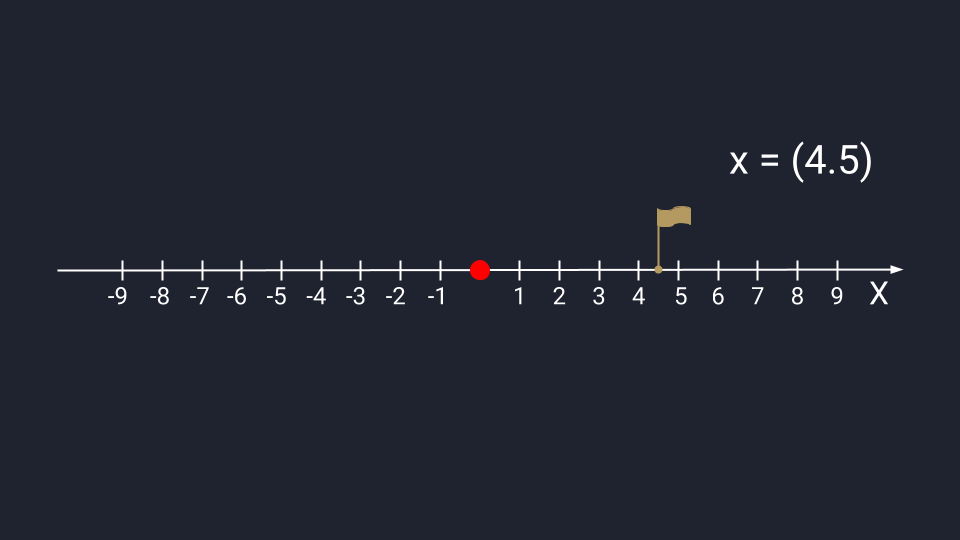
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

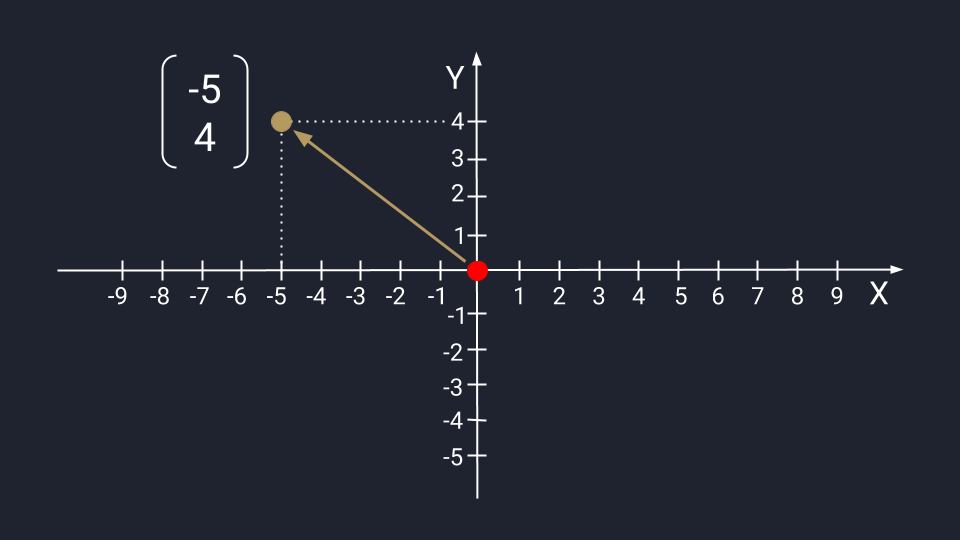
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

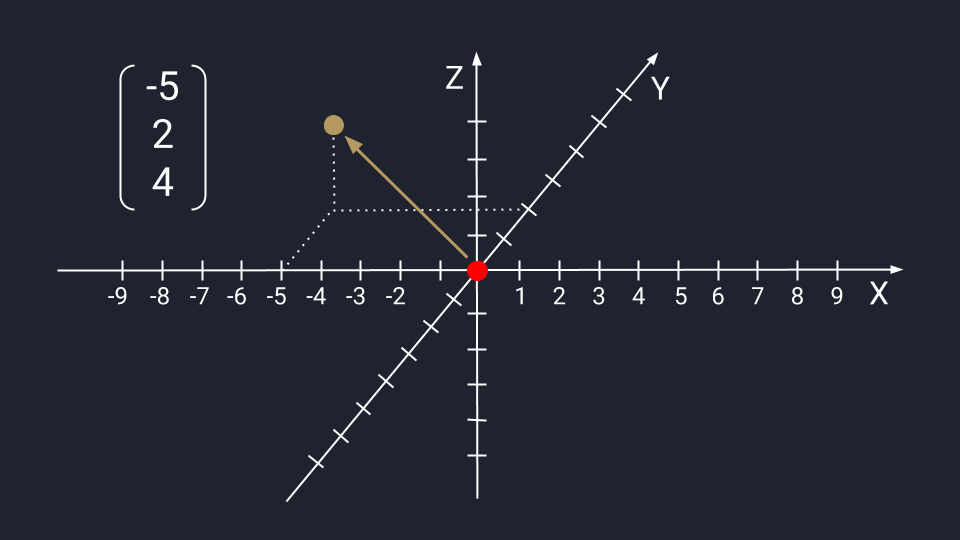
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Вектор: Зачем Он Нужен. Что Такое Вектор? Palsan Показал свое лицо.Скачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:Векторы в физикеСкачать

Проектная работа. Вектор. 9 класс

МБОУ Одинцовская гимназия №13

Проектная работа по теме

Выполнили ученики 9А класса

Руководитель учитель математики

Что такое вектор и действия над векторами.

Векторы в геометрии, в физике, в других науках.

Векторы в повседневной жизни.

С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор.

Далее, в процессе работы над данным проектом, Мы приведём ещё интересные примеры с векторами.

Вообще, мы считаем, что математика – это интереснейшая наука, в познании которой нет границ.

Мы выбрали тему о векторах не случайно, нас очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, мы думаем, что эта тема весьма актуальна. В физике, химии, психологии, биологии, экономике и многих других науках употребляют понятие «вектор».

Цель проекта – подготовить раздел школьной энциклопедии «Вектор».

Задачами д анного проекта являются:

— познакомить с историей возникновения понятия «вектор»;

— дать понятие –вектор, продемонстрировать действий над векторами;

— показать применение векторов в решении задач по геометрии и физике;

— научить видеть необычное в обычном;

— выработать внимательное отношение к окружающему миру.

История возникновения понятия «вектор».

Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а также в технике.

Вектор относительно новое математическое понятие.

Интуитивно вектор понимается как объект, имеющий величину, направление и точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел ( Гаусс, 1831).

Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа.

Гамильтону принадлежат и термин «скаляр», он определил в качестве операций над новыми объектами скалярное и векторное произведение.

Гибсс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.

Образ Гиббса запечатлён в «Галерее славы великих американцев». Его имя присвоено многим величинам и понятиям химической термодинамики: энергия Гиббса, парадокс Гиббса, правило фаз Гиббса, уравнения Гиббса — Гельмгольца, уравнения Гиббса — Дюгема, лемма Гиббса, треугольник Гиббса — Розебома и др.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Почти одновременно с ним исследованиями в том же направлении занимался английский математик — Уильям Кингдон Клиффорд (1845–1879)

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками.

Ве́ктор (от лат. vector , «несущий») — в простейшем случае математический объект , характеризующийся величиной и направлением. В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом [1] .

Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними. Другой распространённый способ записи: выделение символа вектора жирным шрифтом.

Вектор в геометрии естественно сопоставляется переносу ( параллельному переносу ), что, очевидно, проясняет происхождение его названия ( лат. vector , несущий ).

Длина вектора – это и есть длина этого отрезка. Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Единичным называется вектор, длина которого равна 1. Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором. У такого вектора конец и начало совпадают. Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются сонаправленными векторами только тогда, когда их направления совпадают друг другу (направлены в одну сторону): a↑↑b

Противоположно направленные вектора – два коллинеарных вектора a и b называются противоположно направленными векторами, только когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной плоскости или те, которые лежат на одной плоскости. С компланарными векторами мы встретимся в 10-11 классах.

Равные вектора. Вектора a и b будут равными, если они будут лежать на одной либо параллельных прямых и их направления и длины одинаковые. То есть, такой вектор можно перенести параллельно ему в каждое место плоскости. Таким образом, два вектора равны, если они коллинеарные, сонаправленые и имеют одинаковые длины:

Действия над векторами.

Суммой векторов: , …называется вектор, получающийся после ряда последовательных сложений: к вектору прибавляется вектор , к полученному вектору прибавляется вектор и так далее.

Это правило многоугольника или правило цепи, которое формулируется из правила треугольника. Из произвольного начала О откладываем вектор , из точки А ₁ , как из начала, откладываем вектор , из точки А ₂ строим вектор и так далее. Вектор есть сумма векторов .

Теорема. Для любых векторов , справедливы равенства:

1) + = + (переместительный закон).

2) ( + ) + = + ( + ) (сочетательный закон)

Эти законы сложения векторов позволяют нам находить сумму векторов в любом удобном порядке.

Умножение вектора на число

Для векторов существует три вида умножения векторов: скалярное и векторное произведение двух векторов и смешанное произведение трех векторов. Результатом первого и последнего есть число, а результатом векторного произведения – вектор.

Векторы в геометрии.

В геометрии под векторами понимают направленные отрезки. Эту
интерпретацию часто используют в компьютерной графике, строя карты освещения, с помощью нормалей к поверхностям. Так же с помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов, а также объёмы тел: тетраэдра и параллелепипеда. Иногда с вектором отождествляют направление.

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: · = · cos . Если один из векторов нулевой, то скалярное произведение равно нулю.

Таким образом, длина (модуль) произведения векторов численно равна площади параллелограмма, построенного на векторах a и b

Смешанное произведение векторов называется скалярное произведение вектора на векторное произведение векторов и

Геометрический смысл смешанного произведения — модуль смешанного произведения численно равен объему параллелепипеда, образованного векторами ,.

Перечисленные выше свойства векторных операций во многом похожи на свойства сложения и умножения чисел. В этом состоит удобство векторных операций: вычисления с векторами выполняются по хорошо известным правилам. В то же время вектор – геометрический объект, и в определении векторных операций используются такие геометрические понятия, как длина и угол; этим и объясняется польза векторов в геометрии (и её приложений к физике и другим областям знания).

Однако для решения геометрических задач с помощью векторов необходимо прежде всего научиться «переводить» условие геометрической задачи на векторный «язык». После такого «перевода» осуществляются алгебраические вычисления с векторами, а затем полученное векторное решение снова «переводится» на геометрический «язык». В этом и состоит векторное решение геометрических задач.

C помощью векторов решаются задачи геометрии. Многие задачи не могли бы решаться иначе, либо решение их было очень затруднительным.

Приведём примеры некоторых из них:

Задача №2 Найти угол, лежащий против основания равнобедренного треугольника, если медианны, проведённые к боковым сторонам, взаимно перпендикулярны.

Задача №3 Дан равнобедренный треугольник МК N . Из вершины К проведена высота КР. Из вершин М и N проведены медианы MF и NE . КР =80, MN = 40. Найти MF и NE .

Маргарита Алигер, биография которой вызывает искренний интерес у поклонников ее творчества, – знаменитая советская поэтесса, удостоившаяся Сталинской премии второй степени за поэму «Зоя» о бесстрашном подвиге советской девушки Зои Космодемьянской. После семилетки училась в химическом техникуме. С детства писала стихи.

Векторы в физике.

О, физика, наука из наук!
Все впереди!
Как мало за плечами!
Пусть химия нам будет вместо рук,
Пусть станет математика очами .
Не разлучайте этих трех сестер,
Познания всего в подлунном мире.
Тогда лишь будет ум и глаз остер,
И знанье человеческое шире.

Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей.

Немецкий физик, математик и филолог. (1809-1877)

В области физики Грассману принадлежат работы по акустике и магнитному взаимодействию токов. Общие идеи Грассмана об абстрактных векторных пространствах привели его к открытию
важного положения – возможности рассматривать цветовые ощущения как трехмерные векторы, что лежит в основе современного учения о цвете. (Чёрный цвет имеет координаты (0,0,0), каждому цвету можно поставить в соответствие координаты точки трёхмерного пространства.
Интерпретация вектора, как параллельного переноса, позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного

применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число .

Джеймс Клерк Максвелл — английский физик, создатель классической электродинамики, один из
основоположников статистической физики, выдвинул идею электромагнитной природы света, установил первый статистический закон — закон распределения молекул по
скоростям, названный его именем. Альберт Эйнштейн однажды сказал, что » работа Джеймса клерка Максвелла изменила мир навсегда. «Действительно, Максвелл предоставил первую цветную фотографию и заложил основу для будущего развития телевизионных, радиолокационных, микроволновых и инфракрасных технологий.
Но в каждом учебном предмете вектор рассматривается так, как это удобно для изучаемого вопроса, но суть – одна.

Проведём сравнительный анализ понятия “вектор” и действий над векторами в математике и физике.

Мальчик массой 50 кг, стоя на гладком льду, бросает груз массой

8 кг под углом 60 0 к горизонту со скоростью 5 м/с. Какую скорость приобретет мальчик?

На парашютиста массой 90 кг в начале прыжка действует сила сопротивления воздуха, проекции которой на оси координат Х и Y равны 300 Н и 500 Н. Найти равнодействующую всех сил.

Вектор используются везде, даже там, где мы их не замечаем, например в литературе : вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу равна нулю. А сила, как известно, векторная величина.

В химии. Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца. Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее, основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».

Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы. Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

Векторы в экономике

Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора. Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.

Векторы в психологии

На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов. Системно-векторная психология позиционируется не как отрасль классической психологии или определенное течение, а как отдельная наука изучения типологии личности.

Вектор – это симбиоз физиологических и психологических качеств человека. Это — характер, темперамент, здоровье, привычки индивида.

Векторы в повседневной жизни

Мы обратили внимание, что векторы, помимо точных наук, встречаются нам каждый день, т.е. повседневно. Векторы – указатели, которые помогают нам быстро найти тот или иной объект, отдел и сэкономить время, или стрелки дорожных знаков.

Базовое понятие «вектор», рассмотренное нами на уроках геометрии в 9 классе, является основой для изучения, а главное понимания других школьных предметов: физики, химии, биологи, экономики. Мы считаем, что этот раздел математики очень пригодится тем, кто планирует получать образование в любой профессии.

1. Векторы необходимы нам для изучения не только математики, но и других наук.

2. Каждый образованный человек должен знать, что такое вектор, потому что сталкивается с этим понятием не только во время учёбы, но и в повседневной жизни.

Учебник Геометрия 7-9 авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев, Е.Г. Позняк, И.И. Юдина; издательство «Просвещение» 2016

Геометрия: задачи на готовых чертежах для подготовки к ГИА и ЕГЭ: 7-9/Э.Н. Балаян. Изд. 7-е –Ростов н/Д; Феникс, 2015.

Энциклопедический словарь юного математика для среднего и старшего школьного возраста.

Составитель А.П. Савин.- М.: Педагогика,, 1985.-352 с.,ил.

http ^// gruzdoff . ru / wiki /Вектор (математика)