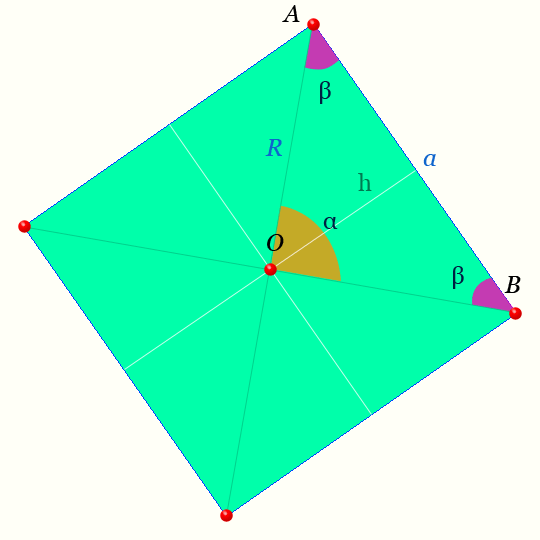
Правильный четырехугольник все формулы

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Правильный четырехугольник

Правильный четырехугольник — это такой четырехугольник у которого все четыре стороны равны и его четыре угла равны. Правильный четырехугольник это квадрат.

Центр правильного четырехугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA , OB — радиусы правильного четырехугольника.

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Обозначения на рисунке для правильного четырехугольника

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Основные формулы для правильного четырехугольника

Периметр правильного четырехугольника

Полупериметр правильного четырехугольника

Центральный угол правильного четырехугольника в радианах

Центральный угол правильного четырехугольника в градусах

Половина внутреннего угла правильного четырехугольника в радианах

Половина внутреннего угла правильного четырехугольника в градусах

Внутренний угол правильного четырехугольника в радианах

Внутренний угол правильного четырехугольника в градусах

Площадь правильного четырехугольника

Или учитывая формулу Площади квадрата получим

Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Правильный многоугольник

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a 1 = a 2 = a 3 = … = a n-1 = a n ,

α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

1. Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
2. Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
3. Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольникаO.
4. Сумма всех углов n-угольника равна: 180° · n — 2
5. Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
7. В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .

Видео:№1080. Докажите, что любой правильный четырехугольник является квадратом.Скачать

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Видео:Запомни: все формулы для площади треугольникаСкачать

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Видео:Свойства правильного шестиугольника. Сравнение площадей. Разбор задачи из стереометрии.Скачать

Площадь четырехугольника

Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

Видео:9 класс, 21 урок, Правильный многоугольникСкачать

Площадь четырехугольника по диагоналям и углу между ними

Видео:Правильные треугольник, четырехугольник и шестиугольник (вывод основных формул)Скачать

Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Видео:23-04 геом 9 правильный четырехугольникСкачать

Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Таблица с формулами площади четырехугольника

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	диагональ и угол между ними
2	стороны и углы между этими сторонами
3	стороны (по Формуле Брахмагупты)
4	стороны и радиус вписанной окружности
5	стороны и углы между ними

Видео:Четырехугольники. Вебинар | МатематикаСкачать

Площадь частных случаев четырехугольников

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

📺 Видео

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Алгебра 7. Урок 4 - Формулы сокращенного умножения и как их запомнить.Скачать