Плотность вероятностей случайного вектора x y имеет вид (5 видео)

Двумерная непрерывная случайная величина

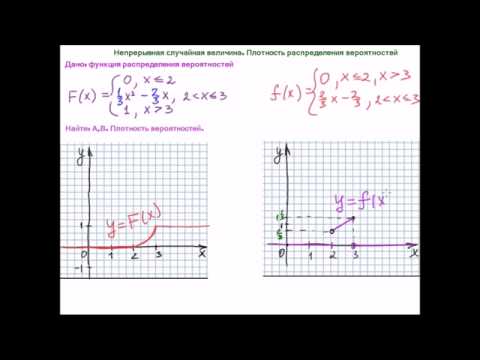
Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю — двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.

Содержание

Система непрерывных случайных величин: теория
Примеры решений
Решебник по теории вероятности онлайн
Распределение случайного вектора
f(x,y) – плотность вероятности случайного вектора (X,Y); fX(x) и fY(y) – плотности вероятностей координат этого вектора
Ваш ответ
решение вопроса
Похожие вопросы
📹 Видео

Видео:Функция распределения и плотность распределенияСкачать

Система непрерывных случайных величин: теория

Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(Xlt x, Ylt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:

Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:

Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:

$$P(x_1 le X le x_2, y_1 le Y le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$

Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:

Если для всех значений $(x,y)$ выполняется равенство

то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:

Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:

В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).

Видео:Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

Примеры решений

Задача 1. Дана плотность распределения вероятностей системы $$ f(x)= left< begin C, mbox O(0,0), A(4,0), B(4,1)\ 0, mbox \ end right. $$ Найти:
$C, rho_1(x), rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_, F(2,10), M[X|Y=1/2]$.

Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ — плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=csqrt, quad A(0;0), B(-1;-1), C(-1;0) $$

Задача 3. Интегральная функция распределения случайного вектора (X,Y): $$ F(x)= left< begin 0, mbox x le 0 mbox yle 0\ (1-e^)(1-e^), mbox x gt 0 mbox ygt 0\ end right. $$ Найти центр рассеивания случайного вектора.

Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У) $$f(x,y)=C e^$$ Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.

Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 sin(x+y)$ в квадрате $0 le x le pi/2$, $0 le y le pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).

Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 le x le pi/2$, $0 le y le pi/2$, если функция распределения системы $F(x,y)=sin x sin y$.

Задача 7. Плотность вероятности системы случайных величин равна $$f(x,y) = c(R-sqrt), quad x^2+y^2 lt R^2.$$ Определить:
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $alt R$, если центры обоих кругов совпадают с началом координат.

Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y $$f(x,y)=frac.$$ Найти величину $с$; определить законы распределения $F_1(x)$, $F_2(y)$, $f_1(x)$, $f_2(y)$, $f(x/y)$; построить графики $F_1(x)$, $F_2(y)$; вычислить моменты $m_x$, $m_y$, $D_x$, $D_y$, $K_$.

Видео:Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Видео:Функция распределения дискретной случайной величиныСкачать

Распределение случайного вектора

Распределения векторных случайных величин представляются теми же основными формами, что и распределения скалярных. В дальнейшем ограничимся рассмотрением этих форм применительно лишь к двумерному случайному вектору (системе двух случайных величин).

Функция вероятности используется только для случайных векторов с дискретными компонентами и обычно задается таблицей, где указываются возможные значения х. и у. компонент X и Y случайного вектора , а также вероятности р(х., у.) всех пар этих значений (табл. 2.3).

Очевидно, что при этом