Правильную пирамиду в основании которой лежит четырехугольник (4 видео)

Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида

Когда человек слышит слово «пирамида», то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .

Содержание

Что такое пирамида в общем случае?
Правильная четырехугольная пирамида
Четыре основных линейных параметра
Площадь и объем фигуры
Свойства правильной усеченной четырехугольной пирамиды
Геометрия. 10 класс
Пирамида
Пирамида
В основании лежит треугольник
В основании лежит четырехугольник
Прямоугольник
Трапеция
Теорема Пифагора
💡 Видео

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Что такое пирамида в общем случае?

В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

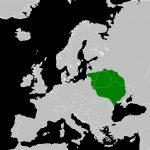
Мы видим что первая фигура имеет треугольное основание, вторая — четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

в основании должен находиться правильный многоугольник;
боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Правильная четырехугольная пирамида

Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Видео:Геометрия 10 класс (Урок№15 - Пирамида.)Скачать

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Видео:Демо-вариант ЕГЭ по математике (базовый уровень) #16-3Скачать

Площадь и объем фигуры

Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

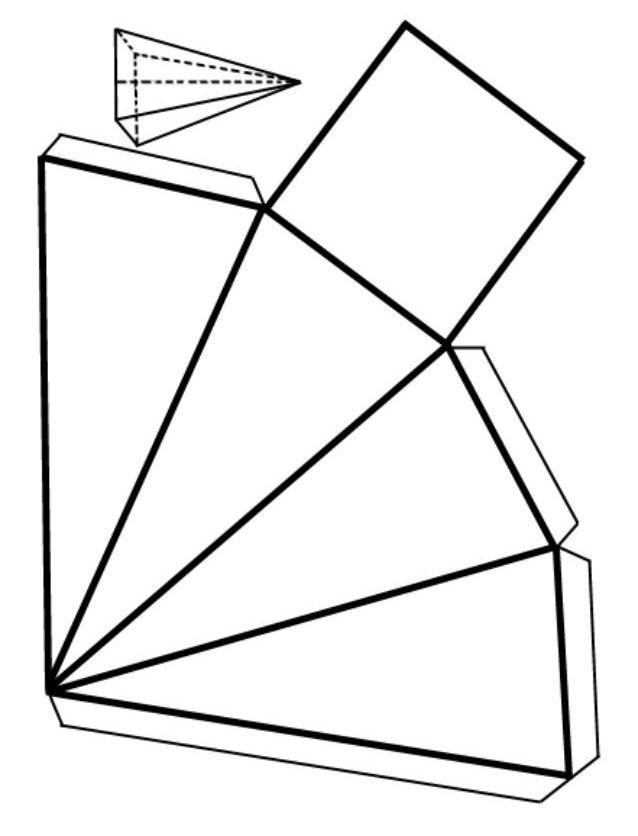
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

Видео:9 класс, 40 урок, ПирамидаСкачать

Свойства правильной усеченной четырехугольной пирамиды

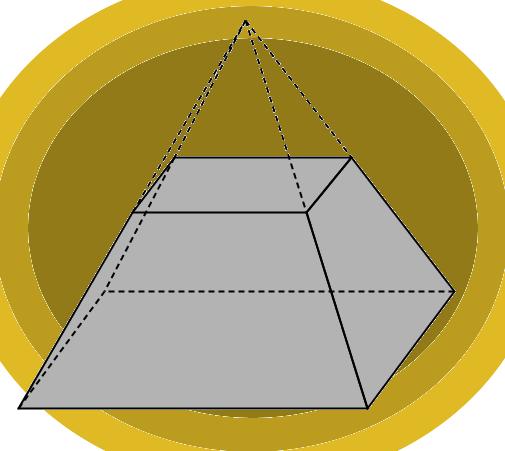
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание — это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Здесь h — расстояние между основаниями фигуры, So1, So2 — площади нижнего и верхнего оснований.

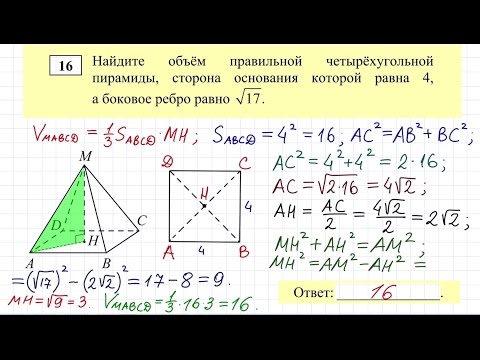
Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Геометрия. 10 класс

Пирамида

Необходимо запомнить

На этом уроке мы ввели понятие пирамиды. Пирамидой будем называть многогранник, составленный из n-угольника и n треугольников, при этом n-угольник называется основанием пирамиды, а треугольники – боковыми гранями. Высотой пирамиды будем называть перпендикуляр, проведенный из вершины пирамиды к плоскости основания. Высота может лежать как внутри пирамиды, так вне ее, в боковой грани или являться ребром.

Название пирамиды зависит от многоугольника, лежащего в основании. Например, пирамида, в основании которой лежит четырехугольник, называется четырехугольной.

Среди пирамид выделяют правильные пирамиды, прямоугольные и усеченные пирамиды.

Также на уроке мы доказали некоторые свойства пирамид, и вывели формулу для вычисления площади боковой поверхности правильной пирамиды.

Пирамида

Пирамиды – одна из загадок человечества. По всему миру было возведено множество пирамид: пирамиды были найдены в Египте, Индии, Мексике и в других странах.

В основном эти постройки выполняли роль храма или усыпальницы. Но почему они имеют именно такую форму? На этот счет ведется много споров, по некоторым из предположений, пирамида – простое в строительстве сооружение, которое отличается от обычных домов, имеющих форму прямоугольного параллелепипеда. Другие утверждают, что пирамида символизирует устремление к солнцу и свету.

Одни из наиболее известных и величественных – пирамиды в Египте.

Размеры пирамиды Хеопса удивляют даже современного человека. Ее основание занимает огромную площадь в 53 тыс. квадратных метров, что соразмерно десяти футбольным полям. Не менее поражают и другие параметры: длина основания – 230 м, длина бокового ребра – столько же, а площадь боковой поверхности – 85,5 тыс. квадратных метров.

Сейчас высота пирамиды Хеопса равна 138 метрам, однако изначально она достигала 147 метров, что можно сравнить с пятидесятиэтажным небоскребом.

На строительство пирамиды пошло около 2 300 000 каменных блоков, объемом свыше 1 м3 каждый.

В настоящее время, чтобы перевезти все камни, из которых сложена пирамида Хеопса понадобится 20 тысяч товарных поездов по 30 вагонов в каждом!

Для площади боковой поверхности усеченной пирамиды верна следующая теорема.

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Площадь боковой поверхности – сумма площадей боковых граней, то есть сумма площадей трапеций. Площадь трапеции вычисляется как произведение полусуммы оснований на высоту. Поскольку трапеции равны, то и длину апофемы d можно вынести за скобки. В скобках останется сумма длин сторон верхнего и нижнего оснований. То есть периметры верхнего и нижнего оснований.

Что и требовалось доказать.

Формула для вычисления площади боковой поверхности усеченной пирамиды будет выглядеть следующим образом:

Видео:Найти площадь поверхности правильной четырехугольной пирамидыСкачать

Пирамида

Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей :

$АВ=an$ — сторона правильного многоугольника

$R$ — радиус описанной окружности

$r$ — радиус вписанной окружности

$n$ — количество сторон и углов

В зависимости от многоугольника, лежащего в основании, пирамиды могут быть треугольными, четырехугольными и т.д.

У треугольной пирамиды есть еще одно название – тетраэдр (четырехгранник).

Формулы вычисления объема и площади поверхности произвольной пирамиды.

Чтобы были понятны формулы, введем обозначения:

$P_$ -периметр основания;

$S_$ — площадь основания;

$S_$ — площадь боковой поверхности;

$S_$ — площадь полной поверхности;

В произвольной пирамиде боковые грани могут быть разными треугольниками, поэтому площадь боковой поверхности равна сумме площадей всех боковых граней, найденных по отдельности.

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.