Поток вектора электрического смещения через замкнутую поверхность (6 видео)

Поток вектора электрического смещения.

Теорема Остроградского — faycca для D

Аналогично потоку для вектора можно ввести

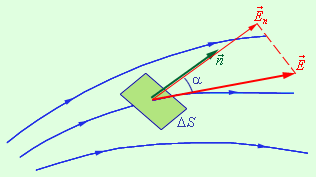
понятие «поток вектора электрического смещения» Ь(Ф_D). Пусть произвольную площадку S пересекают линии вектора электрического смещения D под углом а к нормали п (рис. 1.4.10):

В однородном электростатическом поле Ф₀ = DScosa = D_nS. Теорему Остроградского — Гаусса для вектора D получим из теоремы Остроградского — Гаусса для вектора Е:

так как то

Теорему Остроградского — Гаусса для D можно записать в следующем виде:

Поток вектора D через любую замкнутую поверхность определяют только свободные заряды, а не все заряды внутри объема, ограниченного данной поверхностью. Это позволяет не рассматривать связанные (поляризованные) заряды, влияющие на Ё,_и упрощает решение многих задач. В этом смысл введения вектора D.

Содержание

Изменение Ё и D на границе раздела двух диэлектриков
КОНТРОЛЬНЫЕ ВОПРОСЫ. УПРАЖНЕНИЯ
Теорема Гаусса
Поток вектора напряженности
Теорема Гаусса. Доказательство
Применение теоремы Гаусса
Теорема Гаусса в интегральной форме
Теорема Гаусса в интегральной форме
📺 Видео

Видео:45. Электрическое смещениеСкачать

Изменение Ё и D на границе раздела двух диэлектриков

Рассмотрим простой случай (рис. 1.4.11): два бесконечно протяженных диэлектрика се, и е₂, имеющих общую границу раздела, пронизывает внешнее электростатическое поле Ё₀. Пусть е₂ > е,. Из п. 1.4.3следует,что Е_<п/Е_2п=г₂/г₁ и Е_и = Е_2х.

Образовавшиеся поверхностные заряды изменяют только нормальную составляющую Ё, а тангенциальная составляющая остается постоянной (см. рис. 1.4.11):

т.е. направление вектора Ё изменяется. Это закон преломления вектора напряженности электростатического поля.

— и

Рис. 1.4.11 Рис. 1.4.12

Изменение вектора D и его проекций — D_n и D_x приведены на рис. 1.4.11. _

Так как D = г_пгЁ, то

нормальная составляющая вектора D, не изменяется);

(тангенциальная составляющая

вектора D увеличивается в е₂/е, раз).

Следовательно, закон преломления вектора D имеет следующий вид:

Закон преломления для векторов Ё и D показан на рис. 1.4.13. Как видно из рис. 1.4.13 , при переходе из одной диэлектрической среды в другую вектор D преломляется на тот же угол, что и Ё(5 = ег₀Ё). Входя в диэлектрик с большей диэлектрической проницаемостью, линии D и Ё удаляются от нормали.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

КОНТРОЛЬНЫЕ ВОПРОСЫ. УПРАЖНЕНИЯ

1. Указать виды поляризации.
2. Что показывает диэлектрическая проницаемость среды?
3. Вывести связь между диэлектрической восприимчивостью вещества и проницаемостью среды.
4. В чем различие поляризации диэлектриков с полярными и неполярными молекулами?
5. Есть ли свободные заряды в идеальном диэлектрике?
6. Какие виды поляризуемости существуют?
7. Назвать три основных класса веществ в соответствии с их способностью проводить электрический ток.
8. Определить, где диэлектрическая проницаемость при построении рис. 1 больше, меньше.

9. Что представляет собой вектор электрического смещения?
10. Сформулировать теорему Остроградского — Гаусса для электростатического поля в диэлектрике.
11. Вывести и прокомментировать условия для векторов ? и D на границе раздела двух диэлектрических сред.
12. Сформулируйте закон преломления для векторов Ё л D.

Видео:Поток векторного поля через замкнутую поверхностьСкачать

Теорема Гаусса

Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.

Видео:Билет №31 "Ток смещения"Скачать

Поток вектора напряженности

Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка Δ S .

Элементарный поток вектора напряженности (через площадку S ) – это физическая величина, равная произведению модуля вектора E → , площади Δ S и косинуса угла α между вектором и нормалью к площадке:

Δ Φ = E Δ S cos α = E n Δ S.

В данной формуле E n является модулем нормальной составляющей поля E → .

Рисунок 1 . 3 . 1 . Иллюстрация элементарного потока Δ Φ .

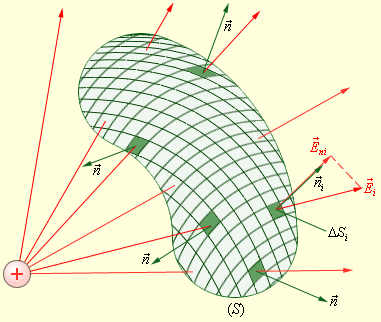
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S . Разобьем заданную поверхность на площадки небольшого размера Δ S i , рассчитаем элементарные потоки Δ Φ i поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1 . 3 . 2 ):

Φ = ∑ ∆ Φ i = ∑ E m ∆ S i

Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.

Рисунок 1 . 3 . 2 . Расчет потока Ф через произвольную замкнутую поверхность S .

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Теорема Гаусса. Доказательство

Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.

Поток вектора напряженности электростатического поля E → через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .

Уравнение Гаусса имеет вид:

Φ = 1 ε 0 ∑ q в н у т р

Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S . В центре заданной поверхности расположен точечный заряд q . Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:

E = E n = 1 4 π ε 0 · q R 2 ,

где R является радиусом сферы.

Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4 π R 2 . Тогда: Φ = 1 ε 0 q .

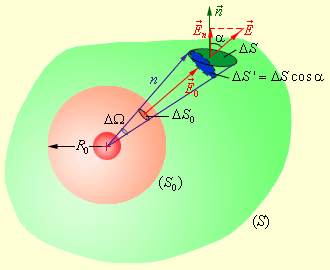
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R 0 (рис. 1 . 3 . 3 ).

Рисунок 1 . 3 . 3 . Поток электрического поля точечного заряда через произвольную поверхность S , окружающую заряд.

Возьмем для рассмотрения конус с малым телесным углом Δ Ω при вершине. Рассматриваемый конус задаст на сфере малую площадку Δ S 0 , а на поверхности S – площадку Δ S . Элементарные потоки Δ Φ 0 и Δ Φ через эти площадки являются одинаковыми. В самом деле:

Δ Φ 0 = E 0 Δ S 0 , Δ Φ = E Δ S cos α = E Δ S ‘ ,

где выражением Δ S ‘ = Δ S cos α определяется площадка, которая задастся конусом с телесным углом Δ Ω на поверхности сферы радиуса n .

Поскольку ∆ S 0 ∆ S ‘ = R 0 2 r 2 , то ∆ Φ 0 = ∆ Φ . Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:

Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q , поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1 . 3 . 2 . Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φ i электрических полей отдельных зарядов. Когда заряд q i расположен внутри поверхности S , он дает вклад в поток, равный q i ε 0 . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.

Так, мы доказали теорему Гаусса.

Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.

Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).

Видео:Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

Применение теоремы Гаусса

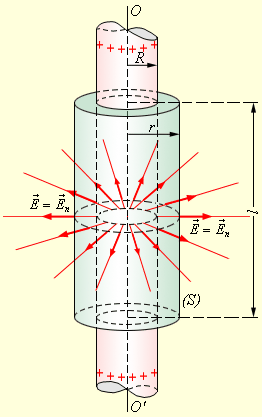
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R . Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l , закрытого с обоих торцов (рис. 1 . 3 . 4 ).

Рисунок 1 . 3 . 4 . Иллюстрация поля однородно заряженного цилиндра. O O ‘ – ось симметрии.

Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:

Φ = E 2 π r l = τ l ε 0 .

В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:

Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.

Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r R . В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ = E 2 π r l . Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.

Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.

К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).

При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.

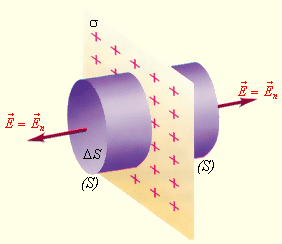
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1 . 3 . 5 ).

Рисунок 1 . 3 . 5 . Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.

Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:

2 E ∆ S = σ ∆ S ε 0 или E = σ 2 ε 0 .

Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.

Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.

Видео:Поток через замкнутую поверхность. Формула Остроградского-ГауссаСкачать

Теорема Гаусса в интегральной форме

Видео:Билет №02 "Теорема Гаусса"Скачать

Теорема Гаусса в интегральной форме

Интегральная форма теоремы Гаусса. Поток вектора электрического смещения через замкнутую поверхность, окружающую конкретный объем, равен алгебраической сумме свободных зарядов на этой поверхности. (13.16)

Поскольку SD = eoerE, теорема Гаусса для однородных и изотропных сред имеет вид (5Åds-, (13.17) J «o *), то есть замкнутая поверхность представляет собой

сумму свободных зарядов на этой поверхности. Людмила Фирмаль

В отличие от теоремы Гаусса (13.17), равной произведенному на eoeg произведению, которое в обоих случаях используется для записи, поток вектора E через замкнутую поверхность является суммой свободных зарядов.

Мало того, что он создается суммой объединенных зарядов на поверхности (связь), замкнутая поверхность равна алгебраической сумме связанных зарядов внутри этой поверхности, взятой с противоположным знаком.

Напомним, что ka и вакуум равны модулю вектора поляризации, на рисунках 402 и b показано положение диполя в поляризованном диэлектрике длиной L, сечение S. Совмещенный заряд находится на обоих концах диэлектрика.

Образуются на их поверхности Плотность обозначена o. Длинные положительные и отрицательные заряды взаимно компенсируются, поэтому заряд os концентрируется на обоих концах, 402, b, длина L * диполя.

учитывая поляризационный диэлектрик Людмила Фирмаль

Электрический момент всего диэлектрика длиной L равен usL, поэтому электрический момент объема диэлектрического блока равен, а плотность связанных зарядов на обоих концах поляризованного диэлектрика равна модулю вектора поляризации P. (Вектор P перпендикулярен ребру.)

Взгляните на диаграмму: 402, c, которая показывает свободный положительный заряд, который вызвал поляризацию окружающего диэлектрика. Рассчитайте некомпенсированный заряд связи, который упал внутри. Некомпенсированный заряд связи — это заряд диполя, который пересекает поверхность $.

Поскольку их поверхностная плотность равна ct, — (f ods— $ Pds, вперед, теорема Гаусса (Уравнение 13.16 или U ^ fx — электростатическое поле

Обратите внимание, что это также относится к определенным условиям и к переменным электромагнитным полям, где точка, где требуется растянуть расстояние от заряда, генерирующего электромагнитное поле, намного короче электромагнитной длины (подробности) (Подробнее см. § 481.) D.

Максвелл расширил теорему Гаусса на переменные электромагнитные поля: уравнения Максвелла (13.17) и (13.17x) имеют разные правые части, или ИЛИ, поэтому уравнение (13.16) имеет вид

Следовательно, eo fÅds Yasvob cfe -g Chsvob 4 и simplicity все еще являются замкнутой поверхностью для зарядов, расположенных в замкнутой поверхности через эту точку, поэтому вся эта поверхность

Если условие равенства точек (симметричное) может быть реализовано, оно используется для определения интенсивности и электрического смещения в любой точке поля. Такие поверхности обычно представляют собой сферы (если заряд представляет собой точку) или стороны цилиндра (если заряд является «линейным»).

Кроме того, из-за симметричного положения всех точек на поверхности относительно заряда значения напряженности поля в разных точках на этой поверхности будут одинаковыми.