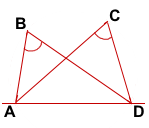
Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности
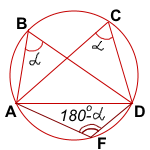
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Видео:ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Метод вспомогательной окружности. 9-й класс
Разделы: Математика
Класс: 9
Один мудрец сказал “ Высшее проявление духа – это разум, Высшее проявление разума – это геометрия, Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою”.
Рассмотрим один из основных геометрических методов решения задач – метод вспомогательной окружности. Предлагаю набор задач, который поможет понять и разобраться в этом методе.
При решении некоторых задач может оказаться полезной следующая теорема.
Т.1 Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:
а) точки М и К расположены по одну сторону от прямой АВ и при этом 0 , то точки А, В, М, К расположены на окружности с диаметром АВ. (Это свойство вписанных углов сформулированное в более удобном виде для решения задач) Сформулированные выше предложения можно назвать свойства четырех точек окружности.
Т1 и Т2 и свойства вписанных углов позволяют решать некоторые интересные геометрические задачи с помощью метода, который называют методом вспомогательной окружности.
Суть метода проиллюстрируем на решении следующих задач.
В треугольнике АВС проведена высота СК. Найти длину отрезка, соединяющего точку К с серединой АС, если АС = 10см.
Проведем высоту АМ, тогда углы АКВ и АМВ равны по 90 0 , значит точки А, К, М, В лежат на одной окружности и АВ – диаметр.(На рисунке окружность изображена штриховой линией, хотя ее можно и вообще не изображать, а “представлять в уме”) Точка О – середина АС по условию
Следовательно, АО = ОВ = КО = r = 5 см. (рис. 3)

Рис. 3
В выпуклом четырехугольнике АВСD диагонали АС и ВD пересекаются в точке О.
0 , 0 , 0 . Найти углы САD и АDС.

Рис. 4
0 – 49 0 = 62 0 .Таким образом В и С лежат по одну сторону от АD и углы АВО и АСD равны значит точки А, В, С, D лежат на одной окружности. 0 , отсюда 0 – 111 0 = 69 0 .
2. дуга АDС равна 222 0 . Значит дуга DС равна 222 0 – 124 0 = 98 0 . Угол САD вписанный и равен 49 0 . Ответ: 0 0
В окружности проведены параллельные хорды АВ, FC, ED известно, что AD ∩ CE = M,
BE ∩FD = N доказать, что МN ║ АВ.
Обозначим равные дуги АF и ВС – α, тогда , то около четырехугольника ARHQ можно описать окружность, приняв отрезок АН за диаметр. Построив ее, замечаем, что 0 , то точки В, Н, А1 и С1 лежат на одной окружности с диаметром ВН. Следовательно, 0 , что и требовалось доказать.
 |  |
б) Рисунок 9 иллюстрирует случай, когда в треугольнике АВС один угол (угол В) тупой. Рассуждение является точно таким же. Только точки В1 и Н как бы меняются местами. В этом случае точка пересечения высот оказывается расположенной вне треугольника.
Для прямоугольного треугольника точкой пересечения высот является вершина прямого угла.
Таким образом, рассмотренные задачи помогают понять суть метода вспомогательной окружности, использование которого помогает решать геометрические задачи.
- И.Ф.Шарыгин. Геометрия Дрофа М.: 2007.
- И.Ф.Шарыгин. Решение задач. Просвещение. М.: 2007.
Видео:Доказать, что точки лежат на одной окружностиСкачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Первое условие принадлежности четырех точек одной окружностиСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:ОГЭ 2021 Задание 24Скачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство 📸 ВидеоОГЭ Задание 25 Условие принадлежности четырёх точек одной окружностиСкачать  2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  ✓ Степень точки в ЕГЭ | Резерв досрока ЕГЭ-2022. Задание 16. Профильный уровень | Борис ТрушинСкачать  2020 точка О центр окружности на которой лежат точки A B и C известно что Угол ABC равен 62 градусаСкачать  Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать  Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать  ВПИСАННЫЙ УГОЛ окружности ТЕОРЕМА 8 класс АтанасянСкачать  16 задание ОГЭ 2024 по математике #маттайм #математикаогэ #окружность #дуги #угол #треугольникСкачать  №8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать  Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  ОКРУЖНОСТЬ (признак принадлежности четырех точек одной окружности) ЧАСТЬ 4Скачать  |