Найдите координаты точек числовой окружности 37п 3 (4 видео)

Найдите координаты точек числовой окружности 37п 3

Вопрос по алгебре:

Найдите координаты точек числовой окружности:
45П/4= 45/4* П= (10+5/4)*П
-37П/3= -37/3* П= (12+1/3)* П
Не понятно действие в скобках, откуда взялось 10 и 5/4? Аналогично и со вторым, объясните.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Содержание

Как написать хороший ответ?
Конспект урока по алгебре 10 класс на тему Числовая окружность на координатной прямой
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
п.2. Числовая окружность
п.3. Градусная и радианная мера угла
п.4. Свойства точки на числовой окружности
п.5. Интервалы и отрезки на числовой окружности
п.6. Примеры
📹 Видео

Ответы и объяснения 1

45П/4= 45/4* П= (10+5/4)*П=5/4*π=π+π/4 3 четверть,
координаты (-√2/2;-√2/2)
45/4=10 5/4=10+5/4

-37П/3= -37/3* П=- (12+1/3)* П=-π/3 4 четверть,
координаты (1/2;-√3/2)
————————————————-
координата х определяется по косинусу угла,а координата у по синусу угла

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Как искать точки на тригонометрической окружности.Скачать

Конспект урока по алгебре 10 класс на тему Числовая окружность на координатной прямой

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

МБОУ Калининская СОШ

анализа 10 класс

«Числовая окружность на координатной плоскости»

Тема Числовая окружность на координатной плоскости

Что будем изучать:
1. Определение.
2. Важные координаты числовой окружности.
3. Как искать координату числовой окружности?
4. Таблица основных координат числовой окружности.
5. Примеры решения задач.
Определение числовой окружности на координатной плоскости

Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
1) при x>0x>0, у>0у>0 – в первой четверти;
2) при х 0у>0 – во второй четверти;
3) при х 0х>0, у Запомните уравнение числовой окружности: x2+y2=1×2+y2=1 .

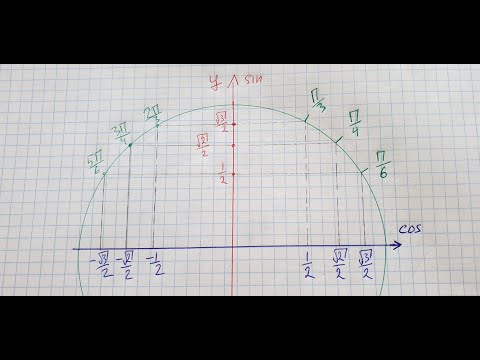
Нам важно научиться находить координаты точек числовой окружности, представленных на рисунке.

Найдем координату точки π4π4

Точка М(π4)М(π4) – середина первой четверти. Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∠ MOP=45° ∠ MOP=45°.
Значит, треугольник OMP – равнобедренный прямоугольный треугольник и OP=MPOP=MP, т.е. у точки M абсцисса и ордината равны: x=yx=y.
Так как координаты точки M(х;y)M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
<x2+y2=1,x=y.<x2+y2=1,x=y.
Решив данную систему, получаем: y=x=√22y=x=22.
Значит, координаты точки M, соответствующей числу π4π4, будут M(π4)=M(√22;√22)M(π4)=M(22;22).
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.
Координаты точек числовой окружности

Пример 1.
Найти координату точки числовой окружности: Р(45π4)Р(45π4).
Решение:
Т.к. числам tt и t+2π ∗ kt+2π ∗ k, где k-целое число, соответствует одна и та же точка числовой окружности то:
45π4=(10+54) ∗ π=10π+5π4=5π4+2π ∗ 545π4=(10+54) ∗ π=10π+5π4=5π4+2π ∗ 5.
Значит, числу 45π445π4 соответствует та же точка числовой окружности, что и числу 5π45π4. Посмотрев значение точки 5π45π4 в таблице, получаем: P(45π4)=P(−√22;−√22)P(45π4)=P(−22;−22).
Пример 2.
Найти координату точки числовой окружности: Р(−37π3)Р(−37π3).
Решение:
Т.к. числам tt и t+2π ∗ kt+2π ∗ k, где k-целое число, соответствует одна и та же точка числовой окружности то:
−37π3=−(12+13) ∗ π=−12π–π3=−π3+2π ∗ (−6)−37π3=−(12+13) ∗ π=−12π–π3=−π3+2π ∗ (−6).
Значит, числу −37π3−37π3 соответствует та же точка числовой окружности, что и числу –π3–π3, а числу –π3π3 соответствует та же точка, что и 5π35π3. Посмотрев значение точки 5π35π3 в таблице, получаем:
P(−37π3)=P(12;−√32)P(−37π3)=P(12;−32).
Пример 3.
Найти на числовой окружности точки с ординатой у=12у=12 и записать, каким числам tt они соответствуют?
Решение:
Прямая у=12у=12 пересекает числовую окружность в точках М и Р. Точка М соответствует числу π6π6 (из данных таблицы). Значит, и любому числу вида: π6+2π ∗ kπ6+2π ∗ k. Точка Р соответствует числу 5π65π6, а значит, и любому числу вида 5π6+2π ∗ k5π6+2π ∗ k.
Получили, как часто говорят в таких случаях, две серии значений:
π6+2π ∗ kπ6+2π ∗ k и 5π6+2π ∗ k5π6+2π ∗ k.
Ответ : t=π6+2π ∗ kt=π6+2π ∗ k и t=5π6+2π ∗ kt=5π6+2π ∗ k.

Пример 4.
Найти на числовой окружности точки с абсциссой x≥−√22x≥−22 и записать, каким числам ttони соответствуют.

Прямая x=−√22x=−22 пересекает числовую окружность в точках М и Р. Неравенству x≥−√22x≥−22соответствуют точки дуги РМ. Точка М соответствует числу 3π43π4 (из данных таблицы). Значит, и любому числу вида −3π4+2π ∗ k−3π4+2π ∗ k. Точка Р соответствует числу −3π4−3π4, а значит, и любому числу вида −3π4+2π ∗ k−3π4+2π ∗ k.

Тогда получим −3π4+2π ∗ k≤t≤3π4+2πk−3π4+2π ∗ k≤t≤3π4+2πk.

Ответ : −3π4+2π ∗ k≤t≤3π4+2πk−3π4+2π ∗ k≤t≤3π4+2πk.
Задачи для самостоятельного решения

Найти координату точки числовой окружности: Р(61π6)Р(61π6).
2) Найти координату точки числовой окружности: Р(−52π3)Р(−52π3).
3) Найти на числовой окружности точки с ординатой у=−12у=−12 и записать, каким числам ttони соответствуют.
4) Найти на числовой окружности точки с ординатой у≥−12у≥−12 и записать, каким числам ttони соответствуют.
5) Найти на числовой окружности точки с абсциссой x≥−√32x≥− 32 и записать, каким числам t t

Домашние задание: красн. учебник § 5, №5.5
№ 5.7-5.8(в,г), №5.10, №5.12-5.13(в,г)

Видео:Координаты точек на числовой окружности. Алгебра 10 класс.Скачать

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Найдите координаты точек числовой окружности 37п 3

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0).
Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0.
Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°.
Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr.
Длина дуги AB: (l_=frac=frac=frac.)
Тогда радианная мера угла: $$ angle AOB=frac<l_>=frac=frac $$

30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
(frac)	(frac)	(frac)	(frac)	(frac)	(frac)	(frac)	(pi)	(frac)	(2pi)

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t).
При t=0, M(0)=A.
При t>0 двигаемся по окружности против часовой стрелки, описывая дугу
⌒ AM=t. Точка M — искомая.
При t Например:

Отметим на числовой окружности точки, соответствующие (frac, frac, frac, frac, pi), а также (-frac, -frac, -frac, -frac, -pi)
Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac, frac, frac), и (-frac).
Все четыре точки совпадают, т.к. begin Mleft(fracright)=Mleft(frac+2pi kright)\ frac-2pi=-frac\ frac+2pi=frac\ frac+4pi=frac end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac+2pi klt tltfrac+2pi k $$
Интервал
$$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac+2pi kleq tleqfrac+2pi k $$
Полуинтервал
$$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac+2pi kleq tltfrac+2pi k $$

п.6. Примеры

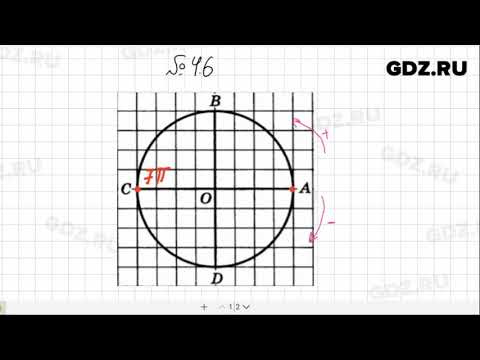
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^=frac.\ EC=60^=frac.\ AE=EC+CD=90^+30^=120^=frac.\ ED=EC+CD=60^+90^=150^=frac. end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; frac; frac; frac).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac=-90^, frac=135^\ frac=210^, frac=315^ end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; 5pi; frac; frac).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π.
Далее – действуем, как в примере 2. begin -frac=fraccdotpi=-6pi+fracrightarrow frac=90^\ 5pi=4pi+pirightarrow pi=180^\ frac=fracpi=3pi-fracrightarrow pi-frac=frac\ frac=fracpi=7pi-fracrightarrow pi-frac=frac end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ fracapprox frac=4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(fraclt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.

$$ frac $$	$$ -frac+2pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ frac+frac $$	$$ -frac $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°