Пошаговое построение орнаментов состоящих из правильных четырехугольников вписывающийся в окружность

Гипермаркет знаний>>Черчение 9 класс>>Черчение: Деление окружности на равные части и построение правильных многоугольников

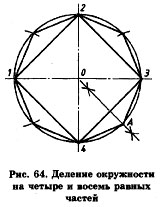
Деление окружности на четыре, восемь равных частей. Построение правильного четырехугольника и восьмиугольника. Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 64).

Для того чтобы разделить окружность на восемь равных частей, необходимо разделить на две равные части дугу, равную 1/4 окружности. Таким образом получим дугу, равную 1/8 окружности (А4 = АЗ). Раствором циркуля, равным АЗ или А4, нанесем засечки на окружности, разделив ее тем самым на восемь равных частей. Последовательно соединив засечки отрезками прямых, получим правильный восьмиугольник.

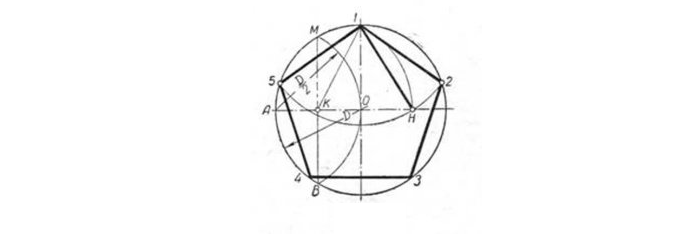
Деление окружности на пять и десять равных частей. Построение правильных пятиугольника и десятиугольника.Чтобы разделить окружность на пять равных частей, находим середину радиуса окружности ОА. Приняв точку В за центр, проведем дугу, радиус которой равен длине отрезка ВС, до пересечения ее с горизонтальным диаметром в точке Е. Отрезок СЕ есть сторона пятиугольника. Отрезок ОЕ соответствует стороне правильного вписанного десятиугольника. Отложив величину, равную 1/5 и 1/10 окружности, разделим ее на пять и десять равных частей. Соединив последовательно засечки (вершины п-угольника) отрезками прямых, получим правильные пяти и десятиугольники (рис. 65)

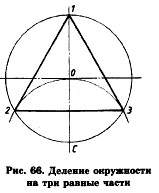
Деление окружности на три, шесть, двенадцать равных частей. Построение правильных многоугольников.Деление окружности на три равные части производится следующим образом. Точка С (рис. 66) принимается за центр, из которого проводится дуга, радиус которой равен радиусу окружности. Проведенная дуга пересечет окружность в точках 2 и 3. Дуги 1-2, 1-3, 2-3 являются третьей частью окружности. Соединив точки 1, 2 и 3, получим правильный треугольник.

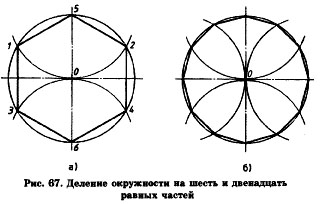
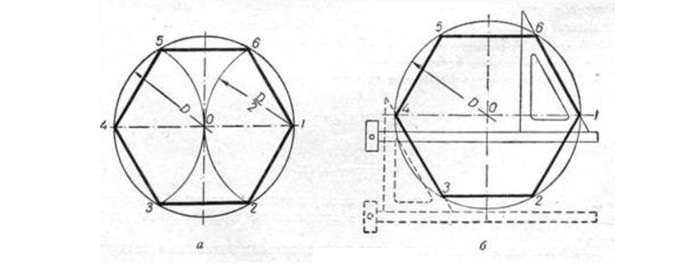
Чтобы разделить окружность на шесть равных частей, от любой ее точки отложим отрезки, равные радиусу окружности (К). Полученные дуги делят окружность на шесть равных частей. Приняв точки 1, 2, 3, 4, 5, 6 за вершины шестиугольника, соединим их отрезками прямых, как показано на рис. 67а. Таким образом построим правильный шестиугольник.

Деление окружности на 6 и 12 равных частей

Деление окружности на двенадцать равных частей основано на откладывании от любой ее точки отрезков, равных половине радиуса окружности (К/2). Полученные дуги разделят окружность на двенадцать равных частей. Приняв каждую засечку за вершину двенадцатиугольника и последовательно соединив их, получим правильный двенадцатиугольник (рис. 67, б).

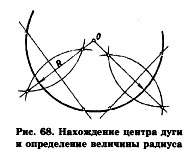
Нахождение центра дуги и определение величины радиуса. В практике выполнения чертежей бывает необходимо найти центр дуги и определить величину ее радиуса. Для этого проводят две непараллельные хорды и восставляют перпендикуляры к их серединам. Точка пересечения перпендикуляров (точка О) есть центр дуги (рис. 68). От центра замеряют величину радиуса дуги.

Вопросы и задания
1.На сколько равных частей можно разделить окружность, используя дугу, проведенную радиусом окружности?
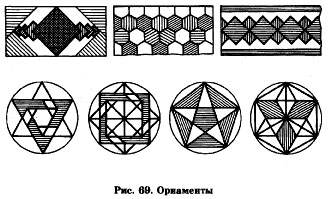
2.На формате А4 выполните один из вариантов орнамента, используя правила деления окружности на равные части. Размеры орнамента произвольные. По желанию можно разработать свой орнамент (рис. 69).

Н.А.Гордеенко, В.В.Степакова — Черчение.,9 класс
Отослано читателями из интернет-сайтов

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Видео:Древний орнамент из окружностейСкачать

Алгоритм построения правильных многоугольников с помощью программы Paint 1. На панели инструментов выберем эллипс. Удерживая клавишу Shift, проведем окружность. — презентация

Презентация была опубликована 6 лет назад пользователемЭдуард Александрович

Похожие презентации

Видео:Геометрия 9 класс (Урок№26 - Построение правильных многоугольников.)Скачать

Презентация на тему: » Алгоритм построения правильных многоугольников с помощью программы Paint 1. На панели инструментов выберем эллипс. Удерживая клавишу Shift, проведем окружность.» — Транскрипт:

1 Алгоритм построения правильных многоугольников с помощью программы Paint 1. На панели инструментов выберем эллипс. Удерживая клавишу Shift, проведем окружность. 2. На панели инструментов выберем прямую линию. Удерживая клавишу Shift, проведем два диаметра, перпендикулярных друг другу. 3. Инструментом «линия» соединяем точки на окружности. Полученная фигура – правильный четырехугольник. 4. Инструментом «линия» проводим два диаметра, перпендикулярных к сторонам квадрата. 5. Соединяем точки на окружности с помощью линии. Полученная фигура – правильный восьмиугольник. 6. Инструментом «линия» проводим диаметры, перпендикулярные сторонам восьмиугольника. 7. Соединяем точки на окружности с помощью «линии». Полученная фигура – правильный 16-ти угольник.

2 Построение 4-х, 8-ми, 16-ти угольников, вписанных в окружность, с помощью программы Paint

3 Алгоритм построения правильных многоугольников с помощью программы Paint 1. На панели инструментов выберем эллипс. Удерживая клавишу Shift, проведем окружность. 2. На панели инструментов выберем прямую линию. Удерживая клавишу Shift, проведем два диаметра, перпендикулярных друг другу. 3. Выделим и скопируем радиус окружности. С помощью данного радиуса отложим две хорд так, чтобы он пересекали диаметр в своей середине и были перпендикулярны одному диаметру. 3. Инструментом «линия» соединяем точки на окружности. Полученная фигура – правильный шестиугольник 4. Инструментом «линия» проводим диаметры, перпендикулярные к сторонам шестиугольника. 5. Соединяем точки на окружности с помощью линии. Полученная фигура – правильный 12-ти угольник 6. Инструментом «линия» проводим диаметры, перпендикулярные сторонам 12-ти угольника. 7. Соединяем точки на окружности с помощью «линии». Полученная фигура – правильный 24-х угольник.

4 Построение 6-ти, 12-ти, 24-х угольников, вписанных в окружность, С помощью программы Paint

Видео:9 класс, 25 урок, Построение правильных многоугольниковСкачать

Построение с помощью циркуля и линейки — описание, алгоритмы и задачи

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Видео:Геометрический орнамент в квадратеСкачать

Построение отрезка, равного данному

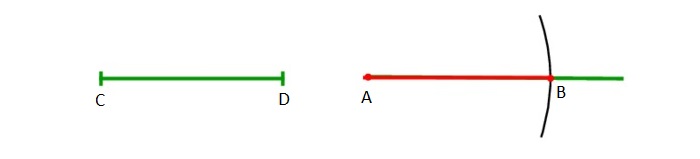
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.

Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Видео:Орнамент народов мира: традиции мастерстваСкачать

Деление отрезка пополам

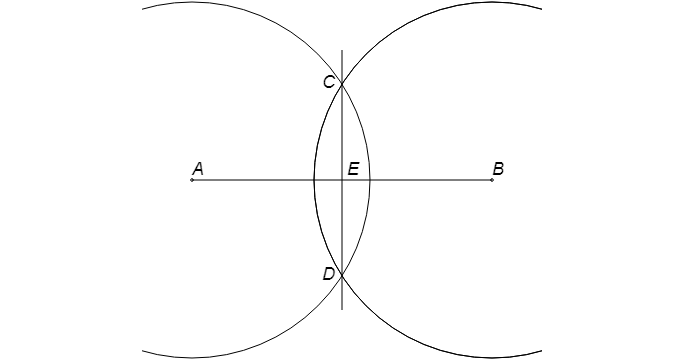
Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Видео:Виды орнаментовСкачать

Построение угла, равного данному

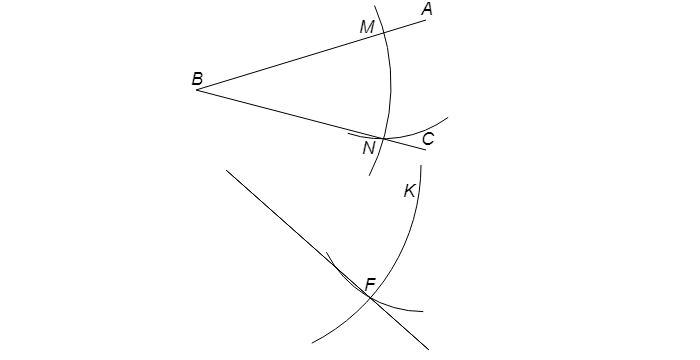
Имеется угол ABC.

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Видео:Орнамент. ПрезентацияСкачать

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O₁ — место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Видео:Урок изо "растительный орнамент"Скачать

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Видео:Орнамент в кругеСкачать

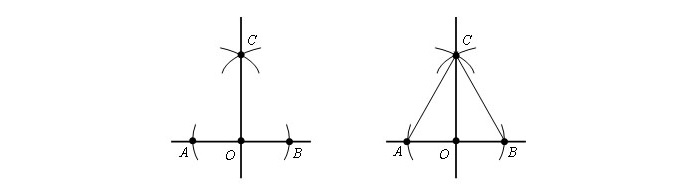
Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

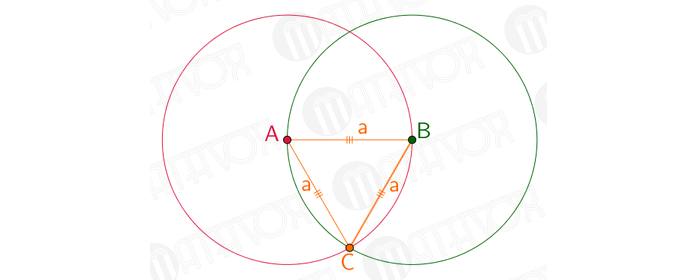
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Видео:Главная тайна Славянских узоров .Об этом вы точно не зналиСкачать

Построение правильного четырехугольника вписанного в окружность

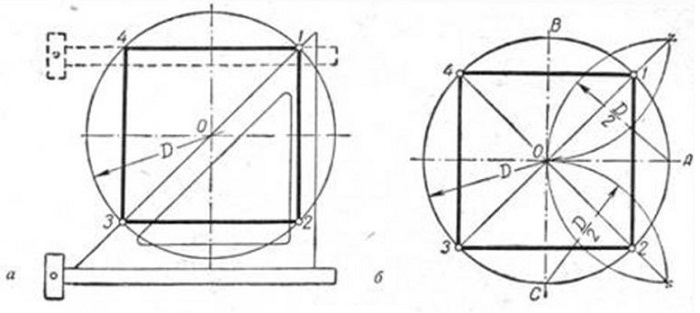
Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

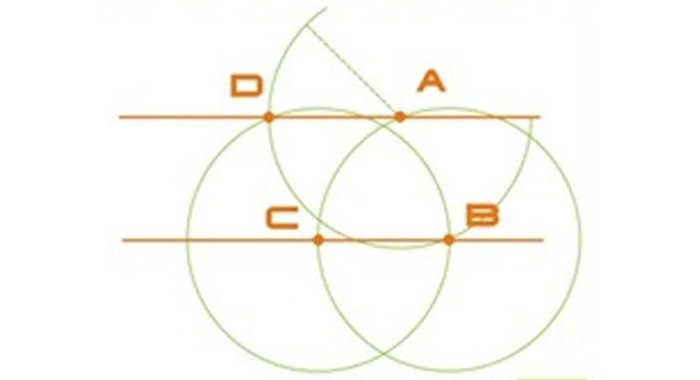
Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Видео:Выправка. Маленький овальный поднос. Цветы на голубом фонеСкачать

Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Видео:Виды орнаментовСкачать

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

🎬 Видео

Виды и построение мусульманского орнамента. Гирих, ислими, куфический каллиграфический стиль, насх.Скачать

Основы рисования. Орнамент. Виды орнаментов.Скачать

Японские орнаментыСкачать

Пэчворк Семинолов - 3 Вида орнамента для начинающихСкачать

Греческий орнамент меандрСкачать

Крымскотатарский орнамент может стать наследием ЮНЕСКОСкачать

22гр.21гр Орнамент геометрический, виды,построение,стилизацияСкачать