Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).
Определение 1. Две прямые на плоскости называются параллельными , если они не пересекаются.
Если прямые a и b параллельны, то это обозначают так:
 . |
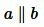На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).
 |
Понятие параллельности можно распространять и на отрезки.
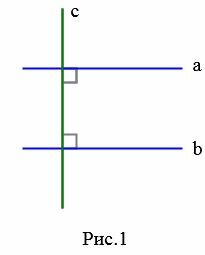
Определение 2. Два отрезка называются параллельными , если они лежат на параллельных прямых (Рис.2).
 |
Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.
    |
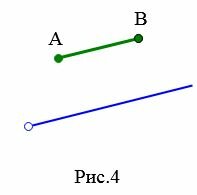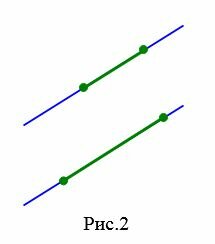
На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать
Признаки параллельности прямых
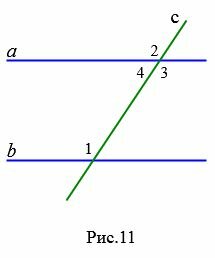
Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):
 |
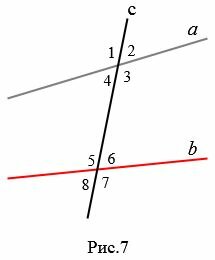- накрест лежащие углы: 3 и 5, 4 и 6;
- односторонние углы: 4 и 5, 3 и 6;
- соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Определим признаки параллельности двух прямых, связанные с этими парамы углов.
Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: 
(Рис.8).
 |
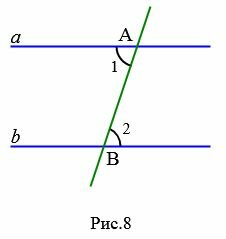Докажем, что .
Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).
 |
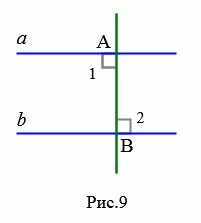Предположим, что углы 1 и 2 не прямые (Рис.10).
 |
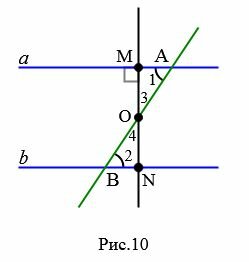Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда 
и 
.
означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны. 
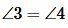
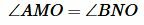
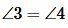
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).
 |
Так как углы 2 и 3 вертикальные, то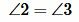 
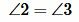
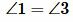
. Тогда из и следует, что 
. Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.
Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например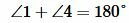 
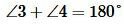
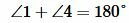
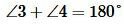
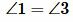
(Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. 
. Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.
Видео:№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать
Параллельны ли прямые a и b если эти прямые перпендикулярны прямой c
1.параллельны ли прямые a и b если прямая a лежит в плоскости не имеющей с прямой b общих точек
2.параллельны ли прямые a и b если эти прямые лежат в параллельных плоскостях
3. параллельны ли прямые a и b если эти прямые перпендикулярны прямой c
4. параллельны ли прямые a и b если эти прямые пересекают плоскость причем точки пересечения не совпадают
Видео:№198. Прямые а и b перпендикулярны к прямой р, прямая с пересекает прямую а. ПересекаетСкачать
Параллельны ли прямые a и b если эти прямые перпендикулярны прямой c
Параллельны ли прямые a и b, если прямая a лежит в плоскости, не имеющей с прямой b общих точек?
Аналоги к заданию № 59: 60 Все
Параллельны ли прямые a и b, если эти прямые лежат в параллельных плоскостях?
Нет, так как по определению прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Аналоги к заданию № 61: 62 Все
Параллельны ли прямые a и b, если эти прямые перпендикулярны прямой c?
Аналоги к заданию № 61: 62 Все
Параллельны ли прямые a и b, если эти прямые пересекают плоскость 
, причём точки пересечения не совпадают?
Нет, так как эти прямые могут иметь общие точки и не лежать в одной плоскости.
📸 Видео
Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать
Перпендикулярные прямые. 6 класс.Скачать
7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать
10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать
7 класс, 25 урок, Признаки параллельности двух прямыхСкачать
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ перпендикулярные к плоскости 10 классСкачать
10 класс, 5 урок, Параллельность трех прямыхСкачать
Параллельные прямые. 6 класс.Скачать
Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать
7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать
Перпендикулярность прямой и плоскости. 10 класс.Скачать
7 класс, 12 урок, Перпендикулярные прямыеСкачать
Теорема 13.1. Две прямые, перпендикулярные третьей прямой, параллельны || Геометрия 7 класс ||Скачать
Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать
Перпендикулярные прямыеСкачать
Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать
Параллельность прямых. 10 класс.Скачать
