Ни шоссейная, ни железная дороги никогда не заворачивают круто, а переходят всегда с одного Направления на другое плавно, без переломов, дугой. Дуга эта обычно есть часть окружности, расположенная так, что прямолинейные части дороги служат касательными к ней. Например, на рис. 82 прямые участки А В и CD дороги соединены дугою ВС так, что АВ и CD касаются (геометрически) этой дуги в точках В и С, т.е. АВ составляет прямой угол с радиусом OB, a CD — такой же угол с радиусом ОС. Делается это, конечно, для того, чтобы путь плавно переходил из прямого направления в кривую часть и обратно.
Рис. 82. Дорожное закругление
Радиус дорожного закругления обыкновенно берется весьма большой — на железных дорогах не менее 600 м; наиболее же обычный радиус закругления на главном железнодорожном пути — 1000 и даже 2000 м.
Видео:Радиус и диаметрСкачать
Радиус закругления
Стоя близ одного из таких закруглений, могли бы вы определить величину его радиуса? Это не так легко, как найти радиус дуги, начерченной на бумаге. На чертеже дело просто: вы проводите две произвольные хорды и из середин их восстанавливаете перпендикуляры: в точке их пересечения лежит, как известно, центр дуги; расстояние его от какой-либо точки кривой и есть искомая длина радиуса.
Но сделать подобное же построение на местности было бы, конечно, очень неудобно: ведь центр закругления лежит в расстоянии 1—2 км от дороги, зачастую в недоступном месте. Можно было бы выполнить построение на плане, но снять закругления на план — тоже нелегкая работа.
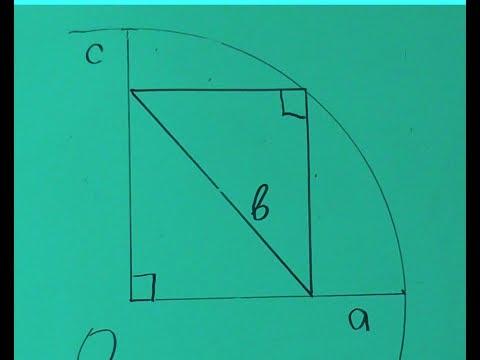
Рис. 83. К вычислению радиуса закругления
Все эти затруднения устраняются, если прибегнуть нс к построению, а к вычислению радиуса. Для этого можно воспользоваться следующим приемом. Дополним (рис. 83) мысленно дугу АВ закругления до окружности. Соединив произвольные точки С и D дуги закругления, измеряем хорду CD, а также «стрелку» EF (т.е. высоту сегмента CED). По этим двум данным уже нетрудно вычислить искомую длину радиуса. Рассматривая прямые CD и диаметр круга как пересекающиеся хорды, обозначим длину хорды через а, длйну стрелки через /г, радиус через R-, имеем:
и искомым радиус
Например, при стрелке в 0,5 м и хорде 48 м искомый радиус
Это вычисление можно упростить, если считать 2R-h равным 2R — вольность позволительная, так как h весьма мало но сравнению с R (ведь R — сотни метров, ah — единицы их). Тогда получается весьма удобная для вычислений приближенная формула
Применив ее в сейчас рассмотренном случае, мы получили бы ту же величину 
Вычислив длину радиуса закругления и зная, кроме того, что центр закругления находится на перпендикуляре к середине хорды, вы можете приблизительно наметить и то место, где должен лежать центр кривой части дороги.
Рис. 84. К вычислению радиуса железнодорожного закругления
Если на дороге уложены рельсы, то нахождение радиуса закругления упрощается. В самом деле, натянув веревку по касательной к внутреннему рельсу, мы получаем хорду дуги наружного рельса, стрелка которой h (рис. 84) равна ширине колеи— 1,52 м. Радиус закругления в таком случае (если а — длина хорды) равен приближенно
При а = 120 м радиус закругления равен 1200 м 1 .
Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать
Радиус закругления окружности это
На рисунке изображён план двухкомнатной квартиры с панорамной лоджией в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна (и остекления лоджии), а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Самое большое по площади помещение — гостиная. В спальне, гостиной и кухне есть двери и окна, выходящие на лоджию, но в кухне окно шире, чем в других комнатах. Остекление лоджии со стороны кухни закруглено. В квартире есть два помещения, в которых нет окон — это прихожая и санузел.
Задание 1. Для помещений, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность пяти цифр.
штук
пачек
м2
м2
Как видно на рисунке справа, требуется знать лишь высоту и длину дуги. Подставьте эти размеры в простую формулу и вычислите радиус. Получив результат, настройте циркуль на этот размер и начертите идеальную дугу требуемого радиуса.
