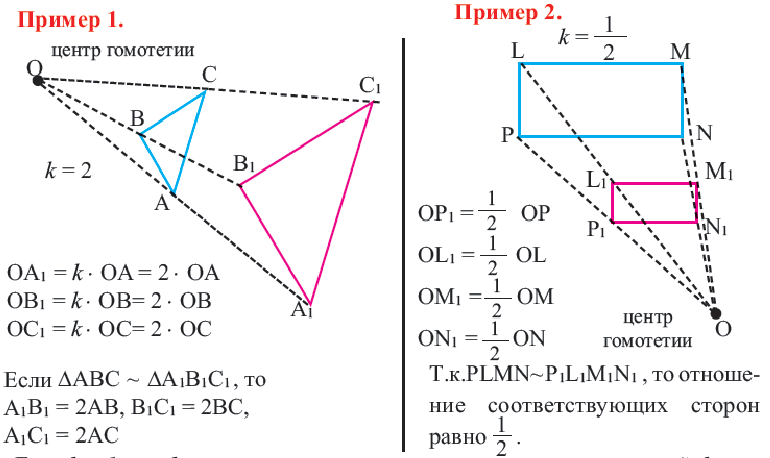
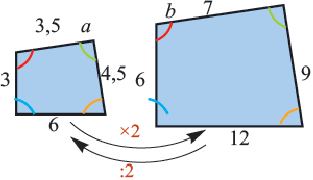
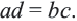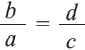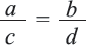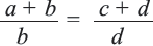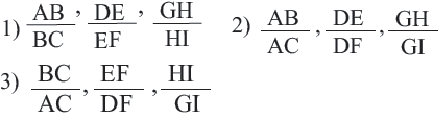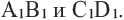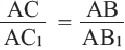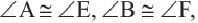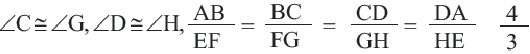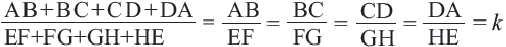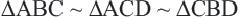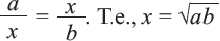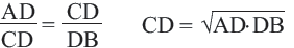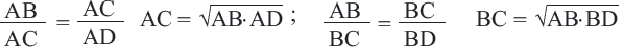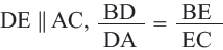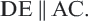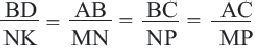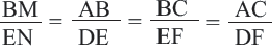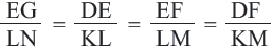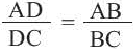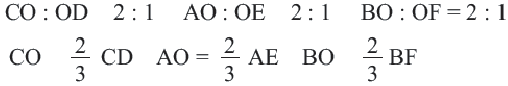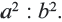Периметры двух подобных многоугольников относятся как 3 : 5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Отношение площадей подобных многоугольников равно квадрату отношения их периметров. Пусть периметр и площадь меньшего многоугольника соответственно равны P1 и S1, периметр и площадь большего многоугольника соответственно равны P2 и S2. Поэтому
- Преобразование фигур в геометрии с примерами решения
- Отношения, пропорция
- Пропорциональные отрезки
- Периметр подобных многоугольников
- Признаки подобия треугольников
- Подобие прямоугольных треугольников
- Применение подобия треугольников
- Высоты, медианы и биссектрисы подобных треугольников
- Свойство биссектрисы треугольника
- Теорема. Свойство медиан треугольника
- Преобразование подобия, гомотетия
- Площади подобных фигур
- Подобие фигур
- Понятие подобия фигур
- Подобие треугольников
- Подобие многоугольников
- 📸 Видео
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Преобразование фигур в геометрии с примерами решения
Содержание:
Отображение плоскости на себя, которое сохраняет расстояния между точками, называется движением. Примерами движения являются такие преобразования, как центральная симметрия, осевая симметрия, поворот (вращение), скольжение.
Поворот:
Пусть, заданы точка О и угол
1. Если точка А не совпадает с точкой О, то
2. Если точка А совпадает с точкой О, то точки 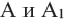
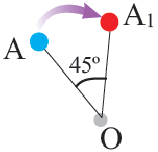
Пример 1. Угол поворота 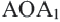
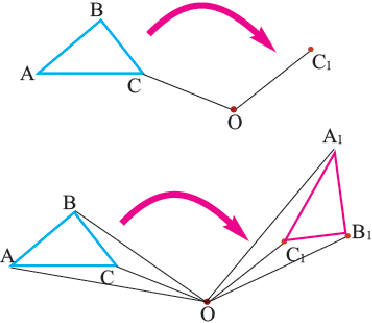
Пример 2. Проанализируйте последовательность шагов, при котором совершается поворот треугольника 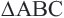
- 1. Соедините точку О и точку С отрезком прямой.
- 2. При помощи транспортира от ОС постройте угол 120° в направлении по часовой стрелке и циркулем отложите отрезок
, конгруэнтный отрезку ОС.
- 3. Потому же правилу соедините точку О с точками А и В. Постройте отрезки
конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки
являются вершинами нового треугольника. Соедините эти точки.
Примечание. Центральная симметрия является поворотом плоскости относительно центра симметрии на 180°.
Исследуйте и начертите в тетради:
На рисунке показана последовательность шагов, которые выполняются при повороте треугольника 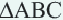
При повороте на угол 90″ в направлении по часовой стрелке координаты вершин изменяются следующим образом.
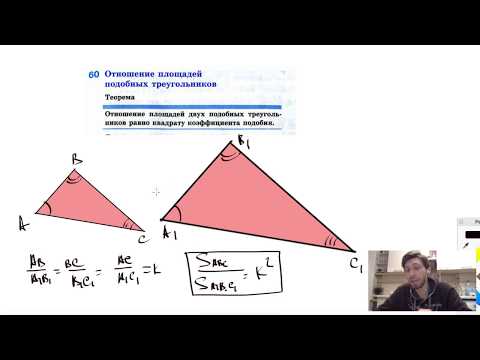
Видео:60. Отношение площадей подобных треугольниковСкачать
Отношения, пропорция
Свойства пропорции
Если 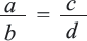
Если 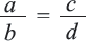
Если 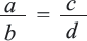
Если 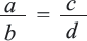
Видео:№544. Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна из сторон второгоСкачать
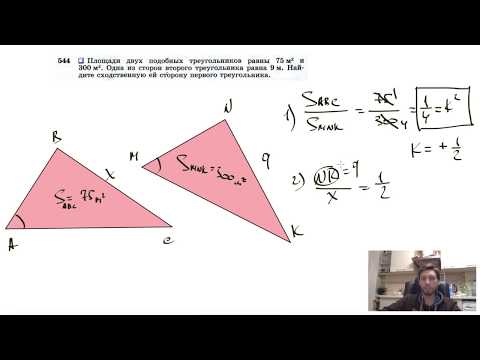
Пропорциональные отрезки
Практическая работа. Пропорциональные отрезки.
1. Начертите в тетради 3 параллельные прямые.
2. Проведите 3 секущие, которые пересекают эти прямые.
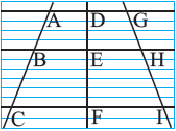
3. Измерьте отрезки АВ, ВС, AC, DE, EF, DF, GH, HI и GI.
4. Запишите и вычислите следующие отношения
5. Можно ли по результатам сказать, что параллельные линии делят секущие на пропорциональные отрезки? Пропорциональные отрезки
Если для отрезков АВ, CD, 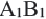
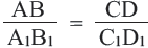
Теорема. Параллельные линии, пересекающие стороны угла, отсекают от них пропорциональные отрезки.
Доказательство. Допустим, что параллельные прямые пересекают стороны угла А в точках В и С, 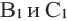
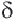
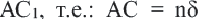
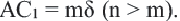
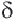
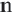
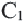
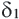
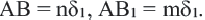
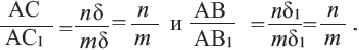
Подобные четырехугольники, подобные треугольники
Подобными называются фигуры одинаковые по форме и у которых соответствующие размеры пропорциональны. Например, все квадраты подобны друг другу, так же как и окружности разных радиусов.
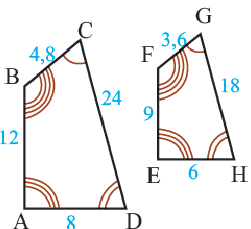
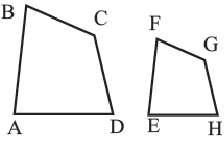
Подобными называются многоугольники, у которых соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Например, на рисунке четырёхугольники ABCD и EFGH являются подобными четырёхугольниками. Так как,
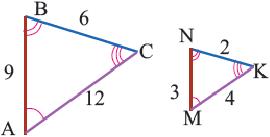
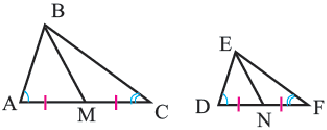
У подобных треугольников соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Здесь, говоря о соответствующих сторонах, имеются в виду стороны, которые находятся напротив конгруэнтных углов. На рисунке для 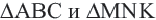
Так как 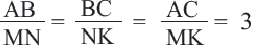
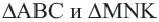
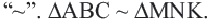
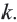
Видео:Отношение площадей подобных треугольниковСкачать

Периметр подобных многоугольников
Теорема. Отношение периметров двух подобных многоугольников равно отношению соответствующих сторон (или коэффициенту подобия)
Если 
Запишите доказательство теоремы, приняв коэффициент подобия за 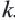
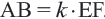
Видео:Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Признаки подобия треугольников
Признак подобия УУ (угол угол)
Если два угла одного треугольника конгруэнтны двум углам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как УУ.
Признак подобия ССС
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как ССС.
Признак подобия СУС
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами конгруэнтны, то такие треугольники подобны. Этот признак подобия коротко записывается как СУС.
Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Подобие прямоугольных треугольников
Высота, проведенная к гипотенузе
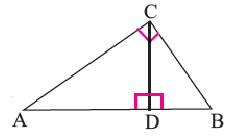
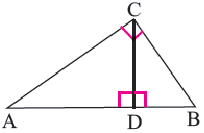
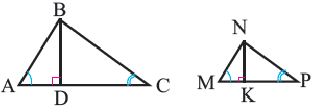
Теорема. Высота, проведённая из вершины прямого угла прямоугольного треугольника, делит его на два подобных треугольника, каждый из которых подобен данному треугольнику.
Доказательство данной теоремы проводится на основании признака подобия УУ Для каждого из трёх треугольников нужно определить два конгруэнтных угла.
Среднее геометрическое
Среднее геометрическое. Для положительных чисел а и b средним геометрическим называется положительное число 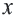
Высота, проведённая из вершины прямого угла на гипотенузу, делит её на два отрезка (на рисунке AD и DB) Здесь отрезки AD и DB являются проекциями катетов АС и ВС на гипотенузу, соответственно.
Следствие 1. Высота прямоугольного треугольника, опущенная из вершины прямого угла есть среднее геометрическое отрезков, на которые она делит гипотенузу.
Следствие 2. Каждый катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу.
Видео:№547. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.Скачать
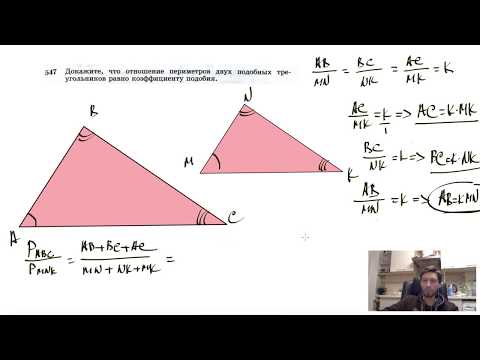
Применение подобия треугольников
Пропорциональные отрезки
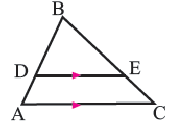
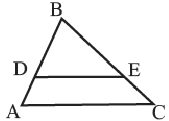
Теорема. Прямая, пересекающая две стороны треугольника, и параллельная третьей стороне делит стороны на пропорциональные отрезки.
Если
Обратная теорема. Если прямая, пересекающая две стороны треугольника делит их на пропорциональные отрезки, то эта прямая параллельна третьей стороне.
Если 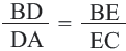
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Высоты, медианы и биссектрисы подобных треугольников
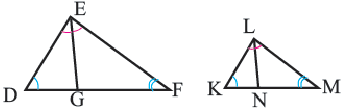
Теорема 1. Если два треугольника подобны, то отношение длин соответствующих высот равны отношению длин соответствующих сторон.
Теорема 2. Если два треугольника подобны, то отношение длин соответствующих медиан равны отношению длин д соответствующих сторон.
Теорема 3. Если два треугольника подобны, то отношение длин соответствующих биссектрис равны отношению длин соответствующих сторон.
Свойство биссектрисы треугольника
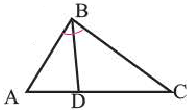
Теорема. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные двум другим сторонам.
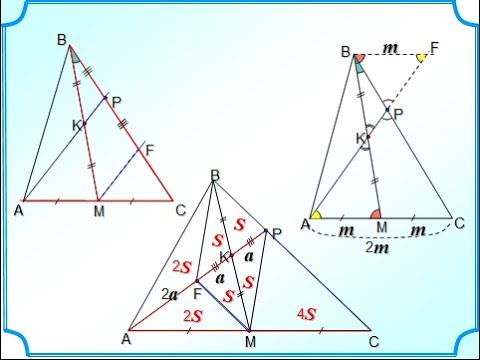
Теорема. Свойство медиан треугольника
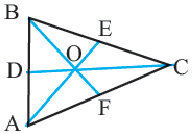
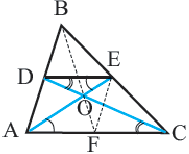
Медианы треугольника пересекаются в одной точке и делятся в точке пересечения в отношении 2:1, начиная от вершины.
Точка пересечения медиан называется центром тяжести треугольника.
Доказательство теоремы представлено в виде двухстолбчатой таблицы.
Дано: 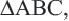
Доказательство: соединим точки O и E.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Преобразование подобия, гомотетия
Гомотетия
Преобразование плоскости на себя, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз называется преобразованием подобия. Фигуры называются подобными, если одна фигура переводится в другую преобразованием подобия. Если при преобразовании подобия точки А и В на плоскости соответственно преобразованы в точки 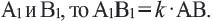
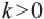
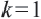
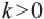
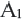
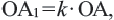
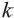
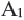
Если 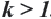
Если 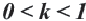
Если 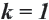
Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента подобия. Например, если отношение соответствующих сторон двух подобных четырёхугольников равно 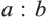
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многоугольник
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:ЕГЭ Задание 16 Отношение площадей подобных треугольниковСкачать

Подобие фигур
Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.
Содержание:
Понятие подобия фигур
В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.
Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.
Для обозначения подобия фигур употребляется знак 



Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.
Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.
Определение. Масштаб — это коэффициент подобия соответствующих фигур.
Подобие треугольников
На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза: 

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: 



Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.
Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.
Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.
Для выявления подобия треугольников существуют признаки подобия треугольников.
Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Следствия из этой теоремы.
1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Подобие многоугольников
Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.
На рисунке 2.436 изображены два подобных пятиугольника 



Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).
Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).
Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
📸 Видео
Отношение площадей подобных треугольников | Геометрия 7-9 класс #58 | ИнфоурокСкачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

8 класс Отношение площадей подобных фигурСкачать

Отношение площадейСкачать

Отношение площадей подобных треугольниковСкачать
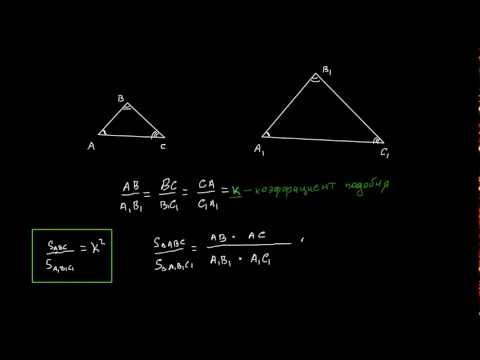
#57. Отношение площадей треугольников — самые надежные отношения!Скачать

ЕГЭ Задание 16 Отношение площадейСкачать

Площади треугольников с равным углом.Скачать

Задание 24 Отношение площадей 3 способа решенияСкачать
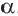
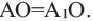
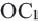 , конгруэнтный отрезку ОС.
, конгруэнтный отрезку ОС.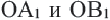 конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки
конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки 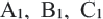 являются вершинами нового треугольника. Соедините эти точки.
являются вершинами нового треугольника. Соедините эти точки.