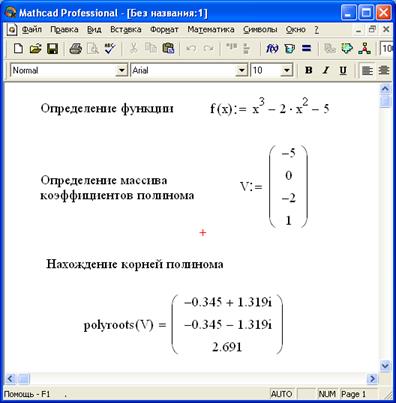
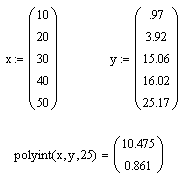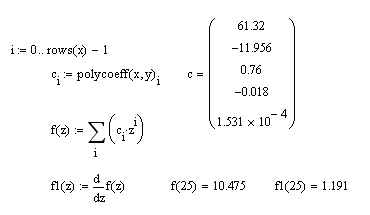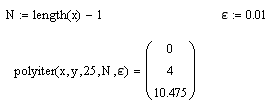Вектор коэффициентов полинома маткад (3 видео)

Функция polyroots в mathcad

Для нахождения корней полинома в MathCAD предназначена специальная функция polyroots (v). Она находит как действительные, так и комплексные корни полинома n-ой степени, коэффициенты которого хранятся в массиве v длиной n+1. Параметром данной функции является вектор-столбец коэффициентов полинома v.

Пример использования функции polyroots показан на рисунке 3.1.4. При решении задачи надо правильно формировать вектор-столбец коэффициентов полинома v, записывая в него значения коэффициентов, начиная коэффициентов при х в нулевой степени.

Решение систем уравнений

Системы уравнений в MathCAD решаются в следующем порядке:

1. Находится приближенное решение системы уравнений. Приближенное решение удобнее всего найти графически;

2. Записывается директива Given, и после нее записываются уравнения системы. Следует помнить, что вместо знака “равно” при записи уравнений используется знак “логическое равенство”, который набирается как + .

3. Записывается любое выражение, использующее функцию Find. Параметрами данной функции являются все переменные, входящие в систему. Функция возвращает вектор-столбец решений системы.

Рисунок 3.1.4 – Нахождение корней полинома при помощи функции

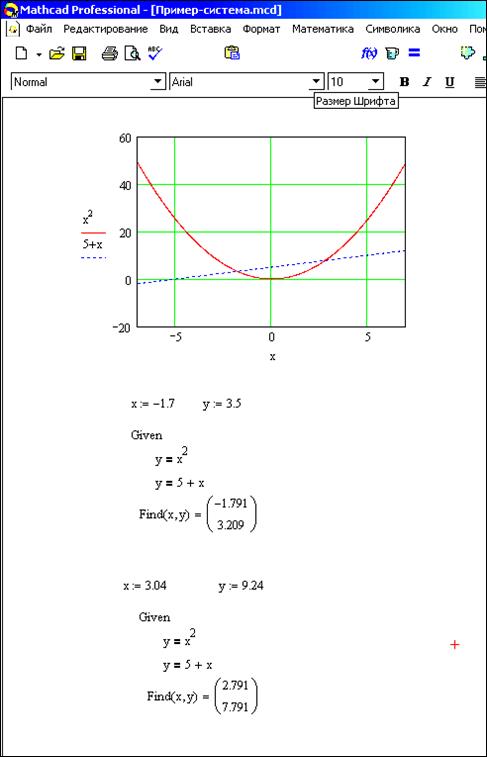
Пример 3.3 Найти решение системы уравнений

Процесс решения данной системы уравнений показан на рисунке 3.2.1

В результате функция Find вернула вектор-столбец и . Это значит, что решением системы уравнений являются значения и .

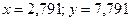
Символьное решение уравнений, неравенств и систем уравнений

Для символьного решения уравнений и неравенств надо выполнить следующее:

1. Вставить в рабочий лист структуру solve c панели инструментов Simbolic.

2. Ввести данные: слева – уравнение или неравенство, справа – переменную, относительно которой требуется его разрешить.

3. Щёлкнуть вне области решения, чтобы получить результат.

Рисунок 3.2.1 – Пример решения системы уравнений

При символьном решении уравнений и неравенств следует вводить знаки =, , находящиеся на панели инструментов Boolean.

При символьном решении системы уравнений после Find надо ввести с панели инструментов Simbolic.

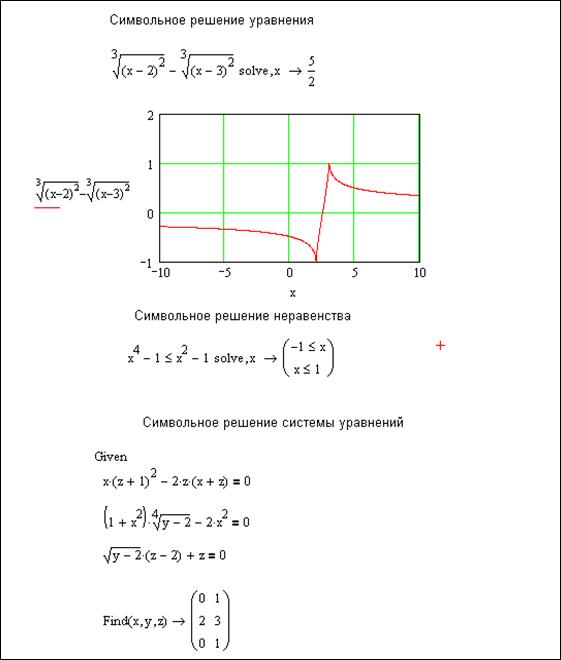
Пример символьного решения уравнений, неравенств и систем уравнений показан на рисунке 3.3.1

Рисунок 3.3.1 – пример символьного решения уравнения, неравенства

и системы уравнений

Некоторые возможности MathCAD

В этом разделе приводятся краткие сведения о возможностях MathCAD, которые могут быть полезны в процессе обучения.

Комплексные числа в MathCAD

MathCAD Воспринимает комплексные числа в форме a+bi, где a и b – вещественные числа. Комплексные числа можно вводить, или получать в результате вычислений. При вводе мнимые числа заканчиваются символом i или j. Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j.

MathCAD содержит следующие операторы и функции для работы с комплексными числами:

Re(z) – вещественная часть z.

Im(z) – мнимая часть z.

arg(z) – угол в комплексной плоскости между вещественной осью и z. Результат заключён между π и –π.

– модуль z. Чтобы записать модуль выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной чертой «|».

– Комплексно сопряжённое к z= a+bi , то есть a-bi. Чтобы применить к выражению этот оператор, выделите его и нажмите клавишу двойные кавычки «”».

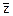
При использовании в комплексной области многие функции являются многозначными. Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.

Рисунок 3.4.1 – Комплексные числа в MathCAD

На рисунке 3.4.1 показан пример использования возможностей MathCADпри работе с комплексными числами.

Последнее изменение этой страницы: 2016-12-28; Нарушение авторского права страницы

Решение уравнений с помощью функции root(f(x),x)

Способы решения уравнений в MathCAD

Форматирование трехмерных графиков

Для форматирования графика необходимо дважды щелкнуть по области построения — появится окно форматирования с несколькими вкладками: Appearance,General,Axes,Lighting,Title,Backplanes,Special, Advanced, Quick Plot Data.

Назначение вкладки Quick Plot Data было рассмотрено выше.

Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.

Во вкладке General (общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display asможно поменять тип графика.

Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On(включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme(схема освещения).

В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x) = 0. Решить уравнение аналитически — значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.

Для решений уравнения с одним неизвестным вида F(x) = 0 существует специальная функция

root(f(x),x),

где f(x) — выражение, равное нулю;

Эта функция возвращает с заданной точностью значение переменной, при котором выражение f(x) равно 0.

Внимание. Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).

Перед использованием функции rootнеобходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.

Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.

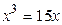
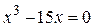
Пример. Решение уравнения с помощью функции root представлено на рисунке 3.1. Перед тем как приступить к решению в системе MathCAD, в уравнении все перенесем в левую часть. Уравнение примет вид: .

Рис. 3.1. Решение уравнения при помощи функции root

Для одновременного нахождения всех корней полинома используют функцию Polyroots(v),где v — вектор коэффициентов полинома, начиная со свободного члена.Нулевые коэффициенты опускать нельзя.В отличие от функции root функция Polyroots не требует начального приближения.

Пример. Решение уравнения 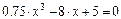с помощью функции polyroots представлено на рисунке 3.2.

Рис. 3.2. Решение уравнения с помощью функции polyroots

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8526 – | 8113 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.

root( f(z), z)

Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.

Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:

Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).

Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 – e x = 0. Левая часть этого выражения и является вторым аргументом функции root
Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).

Напечатайте a=, чтобы увидеть значение корня.

При использовании функции root имейте в виду следующее:

Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
Для выражения с несколькими корнями, например x 2 – 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) – g(x) =0. Для этого функция root может быть использована следующим образом:

Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 1: Использование графика и функции root для поиска корней уравнения.

Что делать, когда функция root не сходится

Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.

Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:

Уравнение не имеет корней.
Корни уравнения расположены далеко от начального приближения.
Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
Выражение имеет разрывы между начальным приближением и корнями.
Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find

Некоторые советы по использованию функции root

В этом разделе приведены несколько советов по использованию функции root:

Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где

Для выражения f(x) с известным корнем a нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x)=0, где h(x)=f(x)/(x-a). Подобный приём полезен для нахождения корней, расположенных близко друг к другу. Часто бывает проще искать корень выражения h(x), определенного выше, чем пробовать искать другой корень уравнения f(x)=0, выбирая различные начальные приближения.

Решение уравнений с параметром

Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.

Рисунок 2: Определение функции пользователя с функцией root.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.

polyroots(v)

Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома.

Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.

Рисунок 4: Использование функции polyroots для поиска корней полинома.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:MathCAD Поиск корней полиномаСкачать

Аппроксимация графика в маткаде

Вводим исходные данные (рис.12).

Рис.12. Фрагмент листа MathCAD с исходными данными

Линейная регрессия

Линейная регрессия в системе MathCAD выполняется по векторам аргумента Х и отсчетов Y функциями:

intercept(X,Y) – вычисляем параметр , смещение линии регресси по вертикали;

slope(X,Y)– вычисляем параметр , угловой коэффициент линии регрессии.

Полученные значения коэффициентов используем в уравнение регрессии .

Функция Corr(Y,y(x)) – вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости [3].

Вычислив параметры линейной регрессии, строим графики исходной функции y и функции линейной регрессии f(x) (рис.13)

Рис. 13. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для линейной аппроксимации

Уравнение линейной регрессии, полученное в MathCAD: y=2.237+3.99.

Полиномиальная регрессия

Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функцией regress(X,Y,n), которая вычисляет вектор S, в составе которого находятся коэффициенты полинома n-й степени.

Значения коэффициентов могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0).

Полученные значения коэффициентов используем в уравнении регрессии .

Вычислив параметры квадратичной регрессии, строим графики исходной функции y и функции квадратичной регрессии f(x) (рис. 14).

Рис.14. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии для квадратичной аппроксимации

Уравнение полиномиальной регрессии : y=2.545+3.852х+0.011

Экспоненциальная регрессия

Для определения экспоненциальной функции решим систему (10) в MathCAD:

Для этого с помощью значков суммирования векторов и векторизации , находящихся на панели векторов и матриц, вычисляем: , , , (рис.15).

Затем составляем матрицы А и В из соответствующих коэффициентов системы линейных уравнений (10) и находим решение системы с помощью встроенной функции lsolve (см. рис. 15).

Решив систему (10), получим значения коэффициентов с и .

Коэффициент вычисляем по формуле: =exp(с).

Полученные значения коэффициентов используем в уравнение регрессии .

Вычислив параметры экспоненциальной регрессии, строим графики исходной функции y и функции экспоненциальной регрессии f(x) (рис. 15).

Рис. 15. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии для экспоненциальной аппроксимации

Уравнение экспоненциальной регрессии: .

Проведенные расчеты показывают, что результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel.

Заключение

Сделаем заключение по результатам полученных данных:

1. В ходе обработки исходных данных средствами функций MS Excel и MathCAD были получены три варианта уравнения аппроксимации: линейная, квадратичная и экспоненциальная.

2. Анализ результатов расчетов показывает, что линейная аппроксимация наилучшим образом описывает экспериментальные данные, так как имеет самый высокий коэффициент детерминированности (0,9960).

Уравнение линейной аппроксимации имеет следующий вид: y=2.237+3.99

3. Совпадение значений величин, полученных на графиках и рассчитанных по формулам в MS Excel, говорит о правильности вычислений.

4. Результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel. Это говорит о верности вычислений.

Список использованной литературы

1. Бердышев В.И., Петрак Л.В. Аппроксимация функций, сжатие численной информации, приложения. – Екатеринбург: УрО РАН, 1999. – 296 с.

2. Малинина Л.А. Основы информатики: Учебник для вузов. – Ростов н/Д.: Феникс, 2006. – 352 с.

3. Макаров Е.Г. MathCAD: Учебный курс. – СПб.: Питер, 2009. – 384 с.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Ответ: Линейная интерполяция осуществляется с помощью встроенной функции linterp, имеющей следующий общий вид: linterp(VX,VY,x), где VX, VY – векторы координат узловых точек; x – значение аргумента, для которого будет получено интерполяционное значение функции y.

В MathCAD для проведения кубической сплайн-интерполяции предлагается три встроенные функции (VX, VY – вектора узловых точек): cspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к кубическому полиному; pspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к параболической кривой; lspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к прямой.

Интерполирующая функция строится с помощью стандартной функции interp, имеющей следующий общий вид: interp(VK,VX, VY,x), где VK – вектор вторых производных сплайна в опорных точках; x – произвольная точка, в которой вычисляется значение интерполирующей функции. Последовательность кубической сплайн-интерполяции такова:

– создаются вектора VX и VY, содержащие координаты точек, через которые нужно провести кубический сплайн;

– вычисляется вектор VK с использованием одной из перечисленных функций;

– вычисляется множество произвольных значений интерполирующей функции в нужном количестве точек с помощью стандартной функции interp.

MathCAD позволяет проводить линейную регрессию общего вида, в которой аппроксимирующая функция задается линейной комбинацией функций, причем сами функции f_i(x) могут быть нелинейными:

Линейная регрессия общего вида реализуется с помощью функции linfit: linfit(VX, VY,F), где VX, VY – координаты исходных точек; F – вектор, содержащий функции f_i(x) , записанные в символьном виде. Функция linfit еще называется функцией аппроксимации по методу наименьших квадратов.

Результатом работы функции linfit является вектор коэффициентов К, при котором среднеквадратичная погрешность приближения исходных точек с координатами VX, VY, минимальна. Вектор VX должен быть возрастающим.

Полиномиальная регрессия позволяет аппроксимировать зависимость полиномом произвольной степени. Вычисление коэффициентов полинома осуществляется с помощью встроенной функции regress, которая имеет следующий общий вид: regress(VX, VY, n), где VX, VY – вектора с координатами исходных данных, n – порядок полинома (первые три возвращаемые коэффициенты служебные, а далее искомые значения, расположенные по возрастанию степени полинома). Для построения аппроксимирующей зависимости можно воспользоваться встроенной функцией interp(VK,VX, VY,x), где VK – вектор коэффициентов, рассчитанных функцией regress; x – рассчитываемая точка. Для проведения регрессии необходимо что бы вектор VX был возрастающим и количество его элементов было больше степени полинома на 1. Функция regress определяет единственный приближающий полином, элементы которого вычисляются по всей совокупности точек. Для выполнения нелинейной регрессии общего вида необходимо определить параметры произвольной аппроксимирующей функции, при которой обеспечивается минимальная среднеквадратичная ошибка. Для этого используется встроенная функцияgenfit,имеющая следующий общий вид: genfit(VX,VY,VS,F), где VS – вектор, который задает начальные приближения элементов вектора K, рассчитываемых итерационным способом; F – вектор, который содержит искомую функцию и ее частные производные по параметрам K_i в аналитическом виде:

На рисунке приведены примеры применения различных видов аппроксимирующих функций в MathCad.

На практике часто бывает, что экономические показатели и данные заданы в виде таблицы значений, однако требуется вывести формулу аналитической функциональной зависимости, чтобы построить математическую модель исследуемого процесса, в экономике в частности.

Для получения линейной зависимости табличных данных в программе MathCad используются следующие функции:

line(x,y) – функция возвращает коэффициенты формулы линейной зависимости в виде вектора. Если линейная зависимость выражается как y=ax+b, то функция возвращает вектор .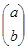

intersept(x,y) – функция возвращает первый коэффициент функции линейной зависимости а.

slope(x,y) –функция возвращает второй коэффициент функции линейной зависимости b.

Для вычисления коэффициента корреляции в MathCad предназначена функция corr(x,y).

Здесь х – массив значений аргумента в табличном представлении, у – массив значений функции в табличном представлении.

Для построения полиномиальной аппроксимирующей зависимостей в MathCad можно воспользоваться функциями regress и interp.

regress(х,у,к) – функция возвращает вектор коэффициентов полинома к-ой степени, подобранного методом наименьших квадратов по табличным значениям х и у. При этом требуется значения аргумента х упорядочить по возрастанию.

interp(s,x,y,t) – функция находит значение полинома в точке t, если получен массив коэффициентов полинома s с помощью функции regress.

Эти две функции позволяют подбирать коэффициенты полинома любой степени.

Задание 3. Имеются сведения о величинах страховых выплат по годам, представленные в табличном виде.

Год	Сумма страховых выплат (руб.)
150 000
200 000
300 000
450 000
450 000
420 000

Требуется исследовать характер изменения величины страховых выплат и подобрать функциональную зависимость для указанных данных, выраженную аналитическим выражением.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 9001 – | 7654 – или читать все.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Видео:ПолиномСкачать

Вектор коэффициентов полинома маткад

Pers.narod.ru. Обучение. Полиномиальная интерполяция в MathCAD

Возможности, описанные в статье, полностью доступны в MathCAD версии 14 и выше. Ссылка на теорию и реализация задачи средствами программирования в MathCAD находятся здесь.

А в современных версиях всё можно сделать с помощью трёх встроенных функций.

Функция polyint(X,Y,x) выполняет полиномиальную интерполяцию по заданным векторам X и Y размерности N в точке x . Она находит полином степени N-1 , проходящий через каждую точку <X_i,Y_i> . Функция возвращает вектор, состоящий из 2 элементов — найденное в точке x значение полинома и оценка погрешности значения.

Проиллюстрируем работу функции, задав векторы X и Y «вручную», а для оценки значения полинома определив точку x=25 .

Функция polycoeff(X,Y) вычисляет коэффиценты интерполяционного полинома и возвращает вектор этих коэффициентов размерностью N для N значений <X_i,Y_i> . В дальнейшем в произвольной точке x значение интерполяционного полинома может быть вычислено по формуле f(x)=Σc_ix_i

Ниже вычисляется значение полинома и его первой производной для тех же векторов исходных данных X , Y и той же точки x=25 .

Функция polyiter(X,Y,x,N,e) позволяет задать значение допустимой погрешности e и максимальную степень полинома N , таким образом, с её помощью можно выполнять полиномиальную интерполяцию более низких степеней. Проверим её работу на степени N-1 .

Более развёрнутый пример с графиками — в приложенном файле MathCAD (формат .XMCD)

Скачать этот пример в формате XMCD (105 Кб)

Ещё одна простая и «ручная» реализация интерполяционного полинома + просто о теории

Во многих случаях анализируемые данные заданы не аналитическим способом (в виде известной функции y(x)), а табличным – когда значения функции известны только для конечного набора значений аргументов y_i=f(x_i), i=1,2,…,N. При этом аналитическая формула для функции f(x_i) нам неизвестна, так что мы не можем достоверно оценить её значение в какой-либо точке кроме тех, что нам известны. Восстановить зависимость по N известным точкам можно из следующих соображений.

Через N различных точек <x_i,y_i>, i=1,2,…,N, всегда можно построить кривую, зависящую от x N -1 :

• прямая может быть построена по 2 точкам (уравнение зависит от x 1 и имеет вид f(x)=c₀+c₁*x);

• парабола может быть построена по 3 точкам (уравнение зависит от x 2 и имеет вид f(x)=c₀+c₁*x+c₂*x 2 );

• в общем виде для N точек уравнение имеет вид f(x)=c₀+c₁*x+c₂*x 2 +…+с_N-1*x N -1 и зависит от x N -1

В этом уравнении нам неизвестны коэффициенты c_i. Из условия, что кривая проходит через все известные точки, можно записать:

c₀ + c₁x₁ + c₂x₁ 2 + …. + c_N-1x₁ N-1 = y₁

или в матричном виде

Решив эту систему уравнений, то есть, найдя обратную матрицу и умножив её на вектор y, найдём коэффициенты c_i. Подставив их в уравнение (1), мы можем аналитически оценить значение функции в любой точке x. Построенная по формуле (1) кривая называется интерполяционным полиномом.

Задание: построить интерполяционный полином по следующим значениям <x_i,y_i>: