Определите вид четырехугольника который является сечением правильной треугольной призмы

Постройте сечение треугольной призмы, проходящее через точки M, N и P. Для случая, когда все рёбра призмы равны, определите вид четырёхугольника, являющегося сечением.

Точки M и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он невидимый, тогда соединяем M и N штрихом. Точки P и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок PN. Он видимый, тогда соединяем P и N сплошной линией. Аналогично строим прямую MP. Треугольник MNP — искомое сечение.

Так как все ребра призмы равны, то треугольник, являющийся сечением — равнобедренный остроугольный.

Видео:10 класс, 30 урок, ПризмаСкачать

Проверочная работа «Призма и пирамида»

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Проверочная работа №8. Вар.1

Верно ли, что основания любой призмы лежат в параллельных плоскостях?

Может ли высота пирамиды быть больше её бокового ребра?

Определите количество сторон многоугольника, лежащего в основании пирамиды , если она имеет семь граней.

Определите вид четырёхугольника (прямоугольник, ромб, трапеция), который является сечением правильной треугольной призмы, если это сечение проходит через ребро нижнего основания и пересекает две стороны верхнего основания.

Могут ли три боковых грани пирамиды быть перпендикулярными к плоскости основания?

Верно ли, что параллелепипед является четырёхугольной призмой?

Может ли площадь боковой поверхности пирамиды быть равной площади её основания?

. В какой призме боковые ребра параллельны ее высоте?

9. Если все ребра призмы равны, будет ли она правильной?

10 . Чем являются боковые грани правильной пирамиды?

11. Постройте усеченную пирамиду, подпишите ее элементы

12. Чему равна площадь боковой поверхности правильной четырёхугольной пирамиды со стороной в основании 4,5см и апофемой 5см? А. 90см 2 Б. 45см 2 В. 101,25см 2

13. Вычислите объём правильной треугольной пирамиды со стороной в основании 6 дм и высотой пирамиды 8дм.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 968 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 338 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Абдуллина Лариса ИвановнаНаписать 1570 09.04.2017

Номер материала: ДБ-347003

09.04.2017 498

09.04.2017 890

09.04.2017 606

09.04.2017 1960

09.04.2017 16865

09.04.2017 842

09.04.2017 867

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:В сосуд, имеющий форму правильной треугольной призмыСкачать

Теоретические самостоятельные работы по геометрии

Теоретические самостоятельные работы по геометрии

Подготовила учитель математики

МОУ Дугдинская СОШ

Проверочная работа №1.

Аксиомы стереометрии и следствия из них

1. Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости?

2. Могут ли две плоскости иметь общую точку, но не иметь общей прямой?

3. Точка А не лежит в плоскости KMN. Назовите прямую пересечения плоскостей AMN и AKM.

4. Даны точки А, В, С и D. Плоскость α проходит через прямую АВ, но не проходит через точку С. Прямые AD и ВС пересекаются в точке В. Сколько данных точек лежит в плоскости α?

5. В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?

6. *Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?

7. *Могут ли три прямые иметь общую точку, но не лежать в одной плоскости?

8. *Три прямые пересекаются в точке А. Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых.

Сколько таких плоскостей можно провести? Рассмотрите все возможные случаи.

одну или бесконечно много

три или не одной

Проверочная работа №2.

Параллельные прямые в пространстве.

Параллельность прямой и плоскости

1. Верно ли, что две параллельные прямые лежат в одной плоскости?

2. Может ли прямая, параллельная плоскости, пересекать какую-либо прямую этой плоскости?

3. Определите взаимное расположение прямой а и плоскости α, если:

a || b и прямая b пересекает плоскость α.

4. Дана плоскость β и прямые а, b, с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если:

а || с , прямые b и с пересекаются, а прямая с лежит в плоскости β.

5. Может ли прямая в пространстве пересекать одну из двух параллельных прямых, но не пересекать другую?

6. Определите взаимное расположение прямой а и плоскости α, если в плоскости α не существует прямой, пересекающей а.

7. Верно ли, что две прямые, параллельные одной плоскости, параллельны?

8. Могут ли прямые AB и CD быть параллельными, если прямые AD и BC пересекаются?

Проверочная работа №3.

Взаимное расположение прямых в пространстве

1. Верно ли, что если две прямые в пространстве не пересекаются, то они параллельны?

2. Может ли угол в пространстве быть тупым?

3. Определите взаимное расположение прямых a и b , если прямая а лежит в плоскости α, а прямая b пересекает плоскость α в точке, не лежащей на прямой а.

4. Прямая l пересекает плоскость треугольника АВС в точке В. Назовите прямую, скрещивающуюся с l и содержащую сторону данного треугольника.

5. Определите, верно ли на плоскости, в пространстве или и на плоскости, и в пространстве данное утверждение:

«Если две различные прямые не пересекаются, то они параллельны.

6. Верно ли, что две прямые, параллельные одной плоскости, могут быть скрещивающимися?

7. Могут ли в пространстве два угла с соответственно параллельными сторонами не быть равными?

8. Определите, какой из случаев взаимного расположения прямых a и b невозможен, если прямая а пересекается с с, а b||с.

Проверочная работа №4.

Тетраэдр и параллелепипед

1. Верно ли, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости?

2. Могут ли рёбра тетраэдра лежать на параллельных прямых?

3. Параллельные плоскости α и β пересекают плоскость γ по прямым a и b соответственно. Определите взаимное расположение прямых a и b .

4. Определите вид сечения параллелепипеда плоскостью, проходящей через середины четырёх боковых рёбер.

5. Дана плоскость α и точка А вне данной плоскости. Определите, какую фигуру в пространстве образуют все прямые, параллельные данной плоскости и проходящие через данную точку. Как расположена эта фигура по отношению к плоскости α?

6. Верно ли, что если в каждой из двух параллельных плоскостей проходит прямая, то эти прямые скрещивающиеся?

7. Может ли в тетраэдре DABC грань DBC содержать прямую, параллельную ребру DA?

8. Плоскость γ пересекает параллельные плоскости α и β по прямым a и b соответственно. Прямая с скрещивается с прямой b . Укажите, какой из случаев взаимного расположения прямых а и с невозможен.

9. Определите, какую фигуру в пространстве образуют середины всех отрезков с концами на двух данных скрещивающихся прямых. Как расположена эта фигура по отношению к данным прямым?

📹 Видео

Задача о вычислении диагонали четырёхугольной призмыСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Построение призмы высотой 30ммСкачать

Как строить сечения тетраэдра и пирамидыСкачать

🔴 В бак, имеющий форму правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Построение сечений Занятие 1Скачать

Построение сечений (часть 1). Пирамиды. сечениеСкачать

Как строить сеченияСкачать

ПРЯМАЯ ПРИЗМА. ЕГЭ. ЗАДАНИЕ 5. СТЕРЕОМЕТРИЯСкачать

Призма. Площадь диагонального сечения. Теорема Пифагора в стереометрии.Скачать

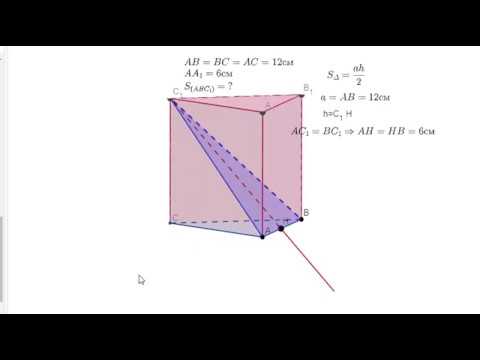
Сечения в треугольной призме Часть 1.Cross-section in a triangular prism Part 1.Скачать

2.1. Призмы. Построение сечений.Скачать