презентация к уроку по геометрии (8 класс) по теме
Диктант можно использовать на уроке систематизации знаний перед контрольной работой. Вопросы диктанта появляются по щелчку левой мыши.
.
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- По теме: методические разработки, презентации и конспекты
- Математические диктанты по геометрии, 8 класс
- Просмотр содержимого документа «Математические диктанты по геометрии, 8 класс»
- Математические диктанты по геометрии (8 класс)
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- 📸 Видео
Видео:Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Скачать:
| Вложение | Размер |
|---|---|
| diktant_po_geometrii.pptx | 40.37 КБ |
Бесплатный марафон подготовки к ЕГЭ на зимних каникулах
Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.
Бесплатно, онлайн, подготовка к ЕГЭ
Предварительный просмотр:
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Подписи к слайдам:
1.Если прямая АВ-касательная к окружности с центром О и В — точка касания, то прямая АВ и … ОВ … 2.Угол АОВ является центральным, если точка О является …, а лучи ОА и ОВ… 3.Вписанный угол, опирающийся на диаметр,…
4.Если хорды АВ И СД пересекаются в точке М, то … 5.Если АВ касательная к окружности, а АД Секущая (А вне окружности, В – точка касания, С и Д точки пересечения секущей с окружностью), то выполняется равенство… 6. Если четырёхугольник АВСД вписан в окружность, то выполняется свойство . 7.Центр окружности, вписанной в треугольник, совпадает с точкой…
8.Если точка А равноудалена от сторон данного угла, то она лежит на … 9.Если точка В лежит на серединном перпендикуляре к отрезку, то она … 10.Около любого … можно описать окружность 11.Если в четырёхугольник можно вписать окружность, то выполняется свойство … 12.Вписанный угол равен … …, на которую … …
Видео:8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

По теме: методические разработки, презентации и конспекты
Урок геометрии в 8 классе по теме «Вписанная и описанная окружность»
Презентация к уроку включает определения основных понятий, создание проблемной ситуации, а также развитие творческих способностей учащихся.
Лабораторная работа по теме «Вписанные и описанные окружности»
Исследуем вопрос об окружностях для треугольников, четырехугольников и правильных многоугольников.
Лабораторная работа по теме «Вписанные и описанные окружности»
Карточка — организатор деятельности по изучению или обобщению темы. Такая работа позволяет анализировать сходства и различия, упрощает понимание и запоминание.
Элективный курс по теме «Вписанные и описанные окружности» для учащихся основной школы
Элективные курсы – это обязательные для посещения курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы.Выполняя функцию внутрипрофильной специализации обучения, электи.
Тест по теме » Вписанная и описанная окружность «
Данный тест проверяет знания учащихся по теме » Вписанная и описанная окружности».
Конспект урока геометрии 8 класс по теме: «Вписанная и описанная окружность» Атанасян.
Конспект урока геометрии 8 класса по теме: «Вписанная и описанная окружность» автор учебника Атанасян.
Тест по теме: «Вписанная и описанная окружности» (8 класс)
Тест по теме: «Вписанная и описанная окружности» (8 класс).
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Математические диктанты по геометрии, 8 класс
Предложенные диктанты адресованы учителям, работающим по учебнику «Геометрия. 8 класс» (авторы А.Г. Мерзляк В.Б. Полонский, М.С. Якир), но могут быть использованы и учителями, работающими по другим учебникам.
Просмотр содержимого документа
«Математические диктанты по геометрии, 8 класс»
Математические диктанты по геометрии
(8 класс, учебник авт. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир)
Диктант 1 по теме «Четырёхугольник и его элементы»
Запишите окончание предложения.
1) Два отрезка называют соседними, если . .
2) Соседними сторонами четырёхугольника называют . .
3) Соседними вершинами четырёхугольника называют . .
4) Противолежащими сторонами четырёхугольника называют . .
5) Противолежащими вершинами четырёхугольника называют . .
6) Периметром четырёхугольника называют . .
7) Диагональю четырёхугольника называют . .
8) Четырёхугольник называют выпуклым, если . .
Сформулируйте теорему о сумме углов четырёхугольника.
Запишите стороны четырёхугольника DEFK, являющиеся соседними со стороной EF.
Запишите сторону четырёхугольника MPON, являющуюся противолежащей стороне MP.
Запишите вершины четырёхугольника BCKD, являющиеся соседними с вершиной D.
Запишите вершину четырёхугольника BCKD, являющуюся противолежащей вершине P.
Начертите четырёхугольник, обозначьте его вершины последовательно буквами A, M, K и F. Запишите какие-либо три обозначения этого четырёхугольника.
Начертите четырёхугольник, у которого один угол тупой, один угол — прямой, а два других — острые.
Начертите четырёхугольник, у которого диагонали перпендикулярны и точкой пересечения делятся пополам.
Чему равен четвёртый угол четырёхугольника, если три его угла равны 50°, 70° и 130°?
Чему равны стороны четырёхугольника, если каждая из них меньше его периметра на 12 см?
Диктант 2 по теме «Параллелограмм. Свойства параллелограмма»
Запишите окончание предложения.
1) Параллелограммом называют . .
2) Высотой параллелограмма называют . .
Сформулируйте свойство противолежащих сторон параллелограмма.
Сформулируйте свойство противолежащих углов параллелограмма.
Сформулируйте свойство диагоналей параллелограмма.
Начертите произвольный треугольник и проведите через каждую его вершину прямую, параллельную противолежащей стороне. Сколько параллелограммов образовалось на рисунке?
Проведите три параллельные прямые и ещё две параллельные прямые, которые пересекаются с первыми тремя прямыми. Сколько параллелограммов образовалось на рисунке?
Найдите периметр параллелограмма, стороны которого равны 16 см и 14 см.
Периметр параллелограмма равен 70 см, а сумма двух его сторон — 50 см. Найдите меньшую сторону параллелограмма.
Сумма трёх сторон параллелограмма равна 40 см. Найдите стороны параллелограмма, если его периметр равен 52 см.
Один из углов параллелограмма равен 20°. Запишите градусные меры трёх остальных его углов.
Сумма двух углов параллелограмма равна 150°. Найдите больший угол параллелограмма.
Найдите углы параллелограмма, если сумма трёх его углов равна 280°.
Верно ли, что любой параллелограмм имеет два угла, сумма которых равна 180°? Ответ обоснуйте.
Верно ли, что любой параллелограмм имеет два острых и два тупых угла? Ответ обоснуйте.
В параллелограмме ABCD ∠B + ∠D
Диагонали параллелограмма ABCD пересекаются в точке O.
1) Какой отрезок является медианой треугольника ABD?
2) Медианой какого треугольника является отрезок DO?
Точка пересечения диагоналей параллелограмма удалена от одной из его вершин на 7 см, а от другой — на 10 см. Какова длина диагоналей параллелограмма?
Диктант 3 по теме «Прямоугольник»
Запишите окончание предложения.
1) Прямоугольником называют . .
2) Параллелограмм является прямоугольником, если один из его углов . .
3) Параллелограмм является прямоугольником, если его диагонали . .
Запишите свойства, которыми обладает прямоугольник как любой параллелограмм.
Запишите свойства прямоугольника, которыми не обладает параллелограмм, отличный от прямоугольника.
Является ли прямоугольником параллелограмм, имеющий прямой угол?
Всякий ли четырёхугольник, имеющий прямой угол, является прямоугольником?
Сделайте рисунок, опровергающий утверждение.
1) Четырёхугольник, имеющий два прямых угла, является прямоугольником.
2) Четырёхугольник, диагонали которого равны, является прямоугольником.
В прямоугольнике ABCD AB = 4 см, AD = 9 см. Чему равно расстояние:
1) от вершины C до прямой AD;
2) от вершины B до прямой CD?
Сумма длин диагоналей прямоугольника равна 15 см. Чему равна длина его диагонали?
Диагональ прямоугольника образует с одной из его сторон угол 24°. Какой угол образует эта диагональ с другой стороной прямоугольника?
Угол между диагоналями прямоугольника равен 40°. Какие углы образует диагональ прямоугольника с его сторонами?
Периметр прямоугольника равен 24 см, а одна из его сторон — 4 см. Найдите сторону прямоугольника, соседнюю с данной его стороной.
Диагонали прямоугольника ABCD пересекаются в точке O, OC = 8 см. Какова длина диагонали BD?
Диктант 4 по теме «Ромб»
Запишите окончание предложения.
1) Ромбом называют . .
2) Параллелограмм является ромбом, если его диагонали . .
3) Параллелограмм является ромбом, если его диагональ . .
Запишите свойства, которыми обладает ромб как любой параллелограмм.
Запишите свойства, которыми не обладает параллелограмм, отличный от ромба.
Диагонали ромба ABCD пересекаются в точке O. Укажите:
1) биссектрису треугольника BCD;
2) медиану треугольника ABC;
3) высоту треугольника ADC.
Угол между диагональю ромба и его стороной равен 24°. Чему равен угол между другой диагональю ромба и той же стороной?
Найдите сторону ромба, если его периметр на 27 см больше этой стороны.
Может ли прямоугольник быть ромбом? Если да, то укажите, в каком случае это возможно.
Может ли диагональ ромба быть перпендикулярной его стороне? Ответ обоснуйте.
Может ли диагональ ромба быть равной его стороне? Ответ обоснуйте.
Периметр ромба ABCD равен 36 см, а его диагональ BD равна 9 см. Какова градусная мера угла C?
Сделайте рисунок, опровергающий утверждение:
1) четырёхугольник, диагонали которого перпендикулярны, является ромбом;
2) четырёхугольник, диагональ которого делит его угол пополам, является ромбом.
Диктант 5 по теме «Квадрат»
Запишите свойства квадрата, которыми не обладает прямоугольник, отличный от квадрата.
Запишите свойства квадрата, которыми не обладает ромб, отличный от квадрата.
Сделайте рисунок, опровергающий утверждение: четырёхугольник, диагонали которого равны и перпендикулярны, является квадратом.
Найдите периметр квадрата, если он на 18 см больше его стороны.
Диагонали квадрата ABCD пересекаются в точке O, BD = 24 см. Чему равна длина отрезка CO?
Как, используя только циркуль, проверить, является ли четырёхугольник квадратом?
Диктант 6 по теме «Средняя линия треугольника»
Запишите окончание предложения.
1) Средней линией треугольника называют . .
2) Средняя линия треугольника, соединяющая середины двух его сторон, параллельна . .
3) Средняя линия треугольника, соединяющая середины двух его сторон, равна . .
Сторона треугольника равна 7 см. Чему равна средняя линия треугольника, параллельная этой стороне?
Точки M, K и N — середины сторон треугольника ABC. Периметр треугольника MKN равен 16 см. Чему равен периметр треугольника ABC?
Чему равен периметр равностороннего треугольника, средняя линия которого равна 6 см?
Существует ли треугольник, в котором две средние линии равны? В случае утвердительного ответа укажите вид этого треугольника.
Существует ли треугольник, в котором все средние линии равны? В случае утвердительного ответа укажите вид этого треугольника.
Сделайте рисунок, опровергающий утверждение: если концы отрезка лежат на двух сторонах треугольника, а длина этого отрезка равна половине третьей стороны, то этот отрезок — средняя линия треугольника.
Диагональ квадрата равна 9 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного квадрата.
Диктант 7 по теме «Трапеция»
Запишите окончание предложения.
1) Трапецией называют четырёхугольник, у которого . .
2) Основаниями трапеции называют . .
3) Боковыми сторонами трапеции называют . .
4) Высотой трапеции называют . .
5) Равнобокой называют трапецию, у которой . .
6) Прямоугольной называют трапецию, у которой . .
7) Средней линией трапеции называют . .
8) Средняя линия трапеции параллельна . .
9) Средняя линия трапеции равна . .
10) Углы при каждом основании равнобокой трапеции . .
11) Диагонали равнобокой трапеции . .
Можно ли утверждать, что четырёхугольник, у которого есть две параллельные стороны, является трапецией? Ответ обоснуйте.
Могут ли быть равными соседние углы трапеции? Ответ обоснуйте.
Могут ли быть равными противолежащие углы трапеции? Ответ обоснуйте.
Существует ли трапеция, у которой:
1) один прямой угол;
2) два прямых угла;
3) один острый угол;
4) два острых угла;
5) один тупой угол;
6) два тупых угла;
7) три тупых угла?
Может ли один из углов при большем основании трапеции быть острым, а другой — тупым? В случае утвердительного ответа изобразите такую трапецию.
Два угла трапеции равны 70° и 150°. Чему равны два других угла трапеции?
Сумма трёх углов равнобокой трапеции равна 220°. Найдите углы трапеции.
Две противолежащие стороны равнобокой трапеции равны 3 см и 7 см, а третья сторона равна 4 см. Чему равен периметр трапеции?
Найдите периметр равнобокой трапеции, боковая сторона которой равна 8 см, а средняя линия — 12 см.
Периметр равнобокой трапеции равен 26 см, а боковая сторона — 6 см. Чему равна средняя линия трапеции?
Диктант 8 по теме «Центральные и вписанные углы»
Запишите окончание предложения.
1) Центральным углом окружности называют . .
2) Градусную меру дуги считают равной градусной мере . .
3) Вписанным углом окружности называют . .
4) Градусная мера вписанного угла равна . .
5) Вписанные углы, опирающиеся на одну и ту же дугу, . .
6) Вписанный угол, опирающийся на диаметр (полуокружность), является . .
Сделайте рисунок, опровергающий утверждение:
1) если вершина угла лежит на окружности, то этот угол является вписанным углом окружности;
2) если стороны угла пересекают окружность, то этот угол является вписанным углом окружности.
3. Начертите окружность произвольного радиуса и какой-либо её вписанный угол DEF. Постройте ещё два вписанных угла, равных углу DEF.
4. Могут ли не быть равными вписанные в одну окружность углы ABC и ADC? В случае утвердительного ответа проиллюстрируйте его рисунком.
5. Могут ли быть равными два вписанных в одну окружность угла, если они не опираются на одну дугу? В случае утвердительного ответа проиллюстрируйте его рисунком.
6. Каким углом, острым, прямым или тупым, является вписанный угол, если дуга, на которую он опирается:
1) больше полуокружности;
2) меньше полуокружности;
3) равна полуокружности?
7. Определите вид вписанного угла, если одна из его сторон проходит через центр окружности.
8. Чему равна градусная мера центрального угла окружности, опирающегося на дугу, которая составляет:
1) 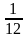
2) 
3) 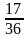
4) 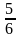
9. Чему равна градусная мера вписанного угла окружности, опирающегося на дугу, которая составляет:
1) 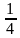
2) 
3) 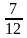
4) 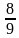
10. Какова градусная мера центрального угла окружности, если он на 40° больше вписанного угла, опирающегося на ту же дугу, что и центральный угол?
Диктант 9 по теме «Описанная и вписанная окружности четырёхугольника»
Запишите окончание предложения.
1) Окружность называют описанной около четырёхугольника, если . .
2) Если четырёхугольник является вписанным в окружность, то сумма его противолежащих углов . .
3) Около четырёхугольника можно описать окружность, если . .
4) Центр описанной окружности четырёхугольника равноудалён от . .
5) Чтобы найти центр описанной окружности четырёхугольника, достаточно найти точку пересечения . .
6) Окружность называют вписанной в четырёхугольник, если . .
7) Если четырёхугольник является описанным около окружности, то сумма его противолежащих сторон . .
8) В выпуклый четырёхугольник можно вписать окружность, если . .
9) Центр вписанной окружности четырёхугольника равноудалён от . .
10) Чтобы найти центр вписанной окружности четырёхугольника, достаточно найти точку пересечения . .
В какой прямоугольник можно вписать окружность?
Можно ли описать окружность около четырёхугольника, у которого только один прямой угол? Ответ обоснуйте.
Можно ли описать окружность около четырёхугольника, у которого только два прямых угла? Ответ обоснуйте.
Можно ли описать окружность около прямоугольной трапеции? Ответ обоснуйте.
Найдите неизвестные углы вписанного четырёхугольника, если два его угла равны 36° и 145°.
Найдите неизвестные углы вписанной трапеции, если один из её углов равен 75°.
Во вписанном в окружность четырёхугольнике ABCD угол C является наименьшим. Какой угол является наибольшим углом этого четырёхугольника?
Около какого ромба можно описать окружность?
Можно ли вписать окружность в трапецию, три стороны которой равны? Ответ обоснуйте.
Найдите периметр четырёхугольника, описанного около окружности, три последовательные стороны которого равны 8 см, 10 см и 13 см.
Три последовательные стороны четырёхугольника, в который вписана окружность, равны 5 см, 6 см и 8 см. Чему равна четвёртая сторона четырёхугольника?
Боковые стороны трапеции, описанной около окружности, равны 12 см и 26 см. Найдите среднюю линию трапеции.
Периметр равнобокой трапеции, описанной около окружности, равен 48 см. Чему равна средняя линия трапеции?
В описанном около окружности четырёхугольнике ABCD сторона BC является наибольшей. Какая сторона является наименьшей стороной этого четырёхугольника?
Радиус окружности, вписанной в трапецию, равен 14 см. Чему равно расстояние между прямыми, на которых лежат основания трапеции?
Диктант 10 по теме «Теорема Фалеса. Теорема о пропорциональных отрезках»
Запишите окончание предложения.
1) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то . .
2) Отношением двух отрезков называют . .
3) Если параллельные прямые пересекают стороны угла, то отрезки, образовавшиеся на одной стороне угла, пропорциональны . .
4) Три медианы треугольника пересекаются в одной точке, которая делит каждую из них . .
5) Биссектриса треугольника делит его сторону на отрезки . .
Три параллельные прямые пересекают стороны угла так, что на одной из его сторон образовались три равных отрезка, а один из отрезков, образовавшийся на второй стороне, равен 12 см. Чему равна сумма длин всех трёх отрезков, образовавшихся на второй стороне?
Три параллельные прямые пересекают стороны угла так, что на одной из его сторон образовались два отрезка длиной 16 см и 28 см, а один из отрезков, образовавшихся на второй стороне, равен 56 см. Найдите неизвестный отрезок, образовавшийся на второй стороне угла. Сколько решений имеет задача?
Точка пересечения медиан треугольника делит одну из медиан на отрезки, один из которых на 6 см больше другого. Какова длина этой медианы?
В каком отношении высоты равностороннего треугольника делятся точкой их пересечения?
Через точку пересечения медиан треугольника проведена прямая, параллельная одной из сторон треугольника. В каком отношении эта прямая делит каждую из двух других сторон треугольника?
Биссектриса равностороннего треугольника равна 12 см. Чему равен радиус окружности, описанной около этого треугольника?
Отрезок AD — биссектриса треугольника ABC, AB AC. Сравните отрезки BD и CD.
Две стороны треугольника равны 20 см и 45 см, а биссектриса угла между ними делит третью сторону на отрезки, меньший из которых равен 16 см. Найдите неизвестную сторону треугольника.
Диктант 11 по теме «Подобные треугольники»
Запишите окончание предложения.
1) Два треугольника называют подобными, если . .
2) Коэффициентом подобия двух подобных треугольников называют число, которое равно . .
3) Любые два равных треугольника подобны с коэффициентом подобия, равным . .
4) Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от . .
Запишите, используя соответствующую символику, что треугольник DEF подобен треугольнику MNK с коэффициентом подобия, равным 4,5.
Начертите какие-нибудь два подобных, но неравных треугольника.
Треугольник ABC подобен треугольнику A1B1C1 с коэффициентом подобия, равным 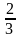
B1C1 = 9 см.
Могут ли быть подобными остроугольный и прямоугольный треугольники? Ответ обоснуйте.
Могут ли быть подобными разносторонний и равнобедренный треугольники? Ответ обоснуйте.
Подобны ли два треугольника, если стороны одного равны 2 см, 3 см и 4 см, а другого — 14 см, 21 см и 32 см? Ответ обоснуйте.
Треугольник ABC подобен треугольнику DEF с коэффициентом подобия, равным 
Треугольник ABC подобен треугольнику A1B1C1 с коэффициентом подобия, равным 1,5. Стороны треугольника A1B1C1 равны 25 см, 20 см и 15 см. Найдите периметр треугольника ABC.
Точки M и K — середины сторон AB и BC треугольника ABC соответственно. Подобны ли треугольники ABC и MBK? Ответ обоснуйте. В случае утвердительного ответа укажите коэффициент подобия.
В треугольнике проведены все средние линии. Сколько образовалось треугольников, подобных данному?
Диктант 12 по теме «Первый признак подобия треугольников»
Сформулируйте первый признак подобия треугольников.
Даны треугольники ABC и DEF. Известно, что ∠A = ∠D, ∠B = ∠E, AB : DE = 3 : 2,
AC = 18 см. Чему равна сторона DF?
Могут ли быть подобными треугольник с углом 20° и треугольник с углом 110°? Ответ обоснуйте.
Могут ли быть подобными треугольник с углом 40° и треугольник с углом 140°? Ответ обоснуйте.
Подобны ли два прямоугольных треугольника, если один из них имеет угол 25°, а другой — 65°? Ответ обоснуйте.
Могут ли быть подобными два треугольника, один из которых равнобедренный, а другой — тупоугольный? Ответ обоснуйте.
Можно ли утверждать, что любые два равнобедренных прямоугольных треугольника подобны? Ответ обоснуйте.
Диктант 13 по теме «Метрические соотношения в прямоугольном треугольнике»
Запишите окончание предложения.
1) Высота прямоугольного треугольника, проведённая к гипотенузе, делит треугольник на . .
2) Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению . .
3) Квадрат катета равен произведению . .
Начертите прямоугольный треугольник, обозначьте его вершины буквами M, K и D, где D — вершина прямого угла. Проведите высоту DA треугольника.
1) Запишите отрезок, являющийся проекцией катета DM на гипотенузу.
2) Запишите отрезок, являющийся проекцией катета DK на гипотенузу.
Проекции катетов прямоугольного треугольника на гипотенузу равны 18 см и 32 см. Найдите меньший катет данного треугольника.
Чему равна высота прямоугольного треугольника, проведённая к гипотенузе, если проекции катетов на гипотенузу равны 2 см и 72 см?
Чему равна гипотенуза прямоугольного треугольника, если один из его катетов равен 6 см, а проекция этого катета на гипотенузу равна 4 см?
Чему равна проекция катета прямоугольного треугольника на гипотенузу, если этот катет равен 9 см, а гипотенуза — 27 см?
Диктант 14 по теме «Тригонометрические функции острого угла прямоугольного треугольника»
Запишите окончание предложения.
1) Синусом острого угла прямоугольного треугольника называют . .
2) Косинусом острого угла прямоугольного треугольника называют . .
3) Тангенсом острого угла прямоугольного треугольника называют . .
4) Котангенсом острого угла прямоугольного треугольника называют . .
5) Синус, косинус, тангенс и котангенс острого угла зависят только от . .
6) Синус и косинус острого угла меньше . .
Запишите тождество, связывающее тангенс, синус и косинус одного и того же угла.
Запишите тождество, связывающее котангенс, синус и косинус одного и того же угла.
Запишите тождество, связывающее тангенс и котангенс одного и того же угла.
Запишите основное тригонометрическое тождество.
Запишите, чему равен:
1) sin (90° − α); 2) cos (90° − α);
3) tg (90° − α); 4) ctg (90° − α).
Запишите, какому числу равен:
1) sin 45°; 2) cos 45°; 3) tg 45°; 4) ctg 45°.
Запишите, какому числу равен:
1) sin 30°; 2) cos 30°; 3) tg 30°; 4) ctg 30°.
Запишите, какому числу равен:
1) sin 60°; 2) cos 60°; 3) tg 60°; 4) ctg 60°.
Известно, что tgα = 
Известно, что cosα = 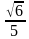
Найдите значение выражения:
1) sin 2 26° + sin 2 64°; 2) tg 2 70°ctg 2 20°.
Стороны прямоугольного треугольника равны 6 см, 8 см и 10 см. Найдите:
1) синус меньшего острого угла треугольника;
2) косинус большего острого угла треугольника;
3) тангенс меньшего острого угла треугольника;
4) котангенс меньшего острого угла треугольника.
Существует ли такой угол α, что:
1) sinα = 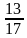
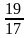
3) tg α= 0,35; 4) ctg α=2000?
В треугольнике DEF с прямым углом D DE DF. Какой из острых углов треугольника имеет:
1) больший синус; 2) больший котангенс?
В треугольнике ABC с прямым углом C sin A = 0,2. Чему равен cos B?
В треугольнике ABC с прямым углом C tg A = 4. Чему равно произведение tg Actg B?
Может ли синус острого угла прямоугольного треугольника быть равным его тангенсу? Ответ обоснуйте.
Синус острого угла вдвое больше его косинуса. Чему равен тангенс данного угла?
Диктант 15 по теме «Решение прямоугольных треугольников»
Запишите окончание предложения.
1) Катет прямоугольного треугольника равен произведению гипотенузы на синус угла, . .
2) Катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, . .
3) Катет прямоугольного треугольника равен произведению другого катета на тангенс угла, . .
4) Катет прямоугольного треугольника равен произведению другого катета на котангенс угла, . .
5) Гипотенуза прямоугольного треугольника равна частному от делению катета на синус . .
6) Гипотенуза прямоугольного треугольника равна частному от делению катета на косинус . .
Можно ли решить прямоугольный треугольник:
1) по двум сторонам;
2) по двум острым углам;
3) по стороне и острому углу?
Чему равен катет прямоугольного треугольника, гипотенуза которого равна 10 см, а прилежащий к искомому катету острый угол — 45°?
Чему равен катет прямоугольного треугольника, второй катет которого равен 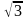
Чему равна гипотенуза прямоугольного треугольника, катет которого равен 2 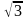
В треугольнике ABC с прямым углом C AC = 12 см, ctg B = 6. Чему равен катет BC?
В треугольнике DEF с прямым углом D EF = 8 см, sin F = 0,4. Чему равен катет DE?
В треугольнике DEF с прямым углом D DE = 8 см, sin F = 0,4. Чему равна гипотенуза EF?
Высота равнобедренного треугольника, проведённая к основанию, равна h, угол при основании треугольника равен β. Чему равно основание треугольника?
Боковая сторона равнобедренного треугольника равна a, угол при вершине треугольника равен α. Чему равна высота треугольника, проведённая к основанию?
Диктант 16 по теме «Многоугольники»
Запишите окончание предложения.
1) Периметром многоугольника называют . .
2) Диагональю многоугольника называют отрезок, соединяющий . .
3) Выпуклым называют многоугольник, все углы которого . .
4) Выпуклый многоугольник расположен в одной полуплоскости относительно . .
5) Сумма углов выпуклого n-угольника равна . .
6) Окружность называют описанной около многоугольника, если . .
7) Около многоугольника можно описать окружность, если существует точка, равноудалённая от . .
8) Если серединные перпендикуляры всех сторон многоугольника пересекаются в одной точке, то . .
9) Окружность называют вписанной в многоугольник, если . .
10) В выпуклый многоугольник можно вписать окружность, если существует точка, равноудалённая от . .
11) Если биссектрисы всех углов выпуклого многоугольника пересекаются в одной точке, то . .
Начертите произвольный выпуклый пятиугольник.
Начертите произвольный пятиугольник, не являющийся выпуклым.
Начертите восьмиугольник, каждый угол которого равен 135°, а каждая сторона —
3 см. Опишите около этого восьмиугольника окружность и впишите в него окружность.
Чему равна сумма углов выпуклого 102-угольника?
Сколько сторон имеет выпуклый многоугольник, сумма углов которого равна 1260°?
Диагональ разбивает выпуклый шестиугольник на два многоугольника, один из которых является четырёхугольником. Определите вид другого многоугольника.
Диагональ разбивает выпуклый n-угольник на два многоугольника, один из которых является треугольником. Определите вид другого многоугольника.
Периметр семиугольника, все стороны которого равны, на 42 см больше его стороны. Чему равна сторона семиугольника?
При каком значении n любой n-угольник является выпуклым?
Диктант 17 по теме «Понятие площади многоугольника. Площадь прямоугольника»
Запишите окончание предложения.
1) Площадью многоугольника называют положительную величину, которая обладает следующими свойствами . .
2) Измерить площадь многоугольника — это значит . .
3) Числовое значение площади называют . .
4) Площадь прямоугольника равна . .
5) Равновеликими называют многоугольники, имеющие . .
Многоугольник разделён на три многоугольника, площади которых равны 10 см 2 ,
20 см 2 и 30 см 2 . Чему равна площадь данного многоугольника?
Найдите площадь прямоугольника, стороны которого равны 0,8 м и 30 см.
Найдите неизвестную сторону прямоугольника, если его площадь и одна из сторон соответственно равны 270 см 2 и 3 дм.
Стороны прямоугольника равны 4 см и 9 см. Чему равна сторона равновеликого ему квадрата?
Сделайте рисунок, опровергающий утверждение: если два прямоугольника имеют равные периметры, то они являются равновеликими.
Верно ли утверждение?
1) Два равновеликих прямоугольника равны.
2) Два равновеликих квадрата равны.
Сторона квадрата равна большей стороне прямоугольника. Какой из этих четырёхугольников имеет бóльшую площадь?
Как изменится площадь квадрата, если его сторону:
2) уменьшить вдвое?
Во сколько раз надо уменьшить сторону квадрата, чтобы его площадь уменьшилась в 36 раз?
Как изменится площадь прямоугольника, если:
1) каждую его сторону увеличить в 4 раза;
2) две его противолежащие стороны уменьшить в 5 раз;
3) две его противолежащие стороны увеличить в 6 раз, а две другие — уменьшить в 3 раза?
Диктант 18 по теме «Площадь параллелограмма»
Запишите окончание предложения.
Площадь параллелограмма равна произведению . .
Запишите формулу, по которой вычисляют площадь S параллелограмма, сторона которого равна a, а проведённая к ней высота — h.
Чему равна площадь параллелограмма, сторона которого равна 12 см, а проведённая к ней высота — 50 мм?
Площадь параллелограмма равна 40 см 2 , а его стороны — 8 см и 10 см. Чему равна бóльшая высота параллелограмма?
Площадь параллелограмма равна 48 см 2 , а его высоты — 4 см и 6 см. Чему равна меньшая сторона параллелограмма?
Диктант 19 по теме «Площадь треугольника»
Запишите окончание предложения.
1) Площадь треугольника равна . .
2) Площадь прямоугольного треугольника равна . .
Запишите формулу, по которой вычисляют площадь S треугольника, сторона которого равна a, а проведённая к ней высота — h.
Запишите формулу, по которой можно вычислить площадь S прямоугольного треугольника, катеты которого равны a и b.
Запишите формулу, по которой можно вычислить площадь S ромба, диагонали которого равны d1 и d2.
Чему равна площадь треугольника, сторона которого равна 18 см, а проведённая к ней высота — 6 см?
Чему равна сторона треугольника, площадь которого равна 20 см 2 , а проведённая к искомой стороне высота — 8 см?
Чему равна высота треугольника, площадь которого равна 24 см 2 , а сторона, к которой проведена искомая высота, — 4 см?
Найдите площадь прямоугольного треугольника, катеты которого равны 20 см и 30 см.
Чему равна площадь ромба, диагонали которого равны 6 см и 14 см?
Сторона и проведённая к ней высота треугольника равны соответственно стороне и проведённой к ней высоте параллелограмма. Чему равно отношение площади данного треугольника к площади параллелограмма?
Площадь треугольника ABC равна 64 см 2 , отрезок BM — медиана этого треугольника. Чему равна площадь треугольника ABM?
Может ли биссектриса треугольника делить его на два равновеликих треугольника? Ответ обоснуйте.
Может ли высота треугольника делить его на два равновеликих треугольника? Ответ обоснуйте.
Что такое геометрическое место точек, являющихся вершинами равновеликих треугольников, имеющих общую сторону AB?
Диктант 20 по теме «Площадь трапеции»
Запишите окончание предложения.
Площадь трапеции равна произведению . .
Запишите формулу, по которой вычисляют площадь S трапеции, основания которой равны a и b, а высота — h.
Чему равна площадь трапеции, основания которой равны 7 см и 8 см, а высота — 6 см?
Найдите высоту трапеции, основания которой равны 6 см и 14 см, а площадь — 90 см 2 .
Найдите среднюю линию трапеции, площадь которой равна 40 см 2 , а высота — 8 см.
Высота равнобокой трапеции, равная 10 см и проведённая из вершины тупого угла трапеции, делит её основание на отрезки, больший из которых равен 21 см. Чему равна площадь трапеции?
Боковые стороны прямоугольной трапеции, в которую можно вписать окружность, равны 8 см и 12 см. Чему равна площадь трапеции?
Боковая сторона равнобокой трапеции, в которую можно вписать окружность, равна
9 см, а площадь трапеции — 72 см 2 . Найдите радиус окружности, вписанной в трапецию.
Диагональ равнобокой трапеции равна 6 см. Чему равна площадь трапеции, если её диагонали перпендикулярны?
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Математические диктанты по геометрии (8 класс)
Видео:ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
У многоугольника стороны могут пересекаться, а могут не пересекаться.
Смежные отрезки многоугольника лежат на одной прямой.
Две смежные стороны многоугольника имеют одну общую вершину.
Название многоугольника зависит от количества вершин.
Количество сторон многоугольника не зависит от количества его вершин.
Периметр многоугольника – это сумма длин всех его сторон.
Соседние вершины многоугольника лежат на разных сторонах.
Отрезок, соединяющий любые две соседние вершины, называют диагональю многоугольника.
Любой многоугольник разделяет плоскость на внешнюю и внутреннюю области.
Многоугольник состоит из сторон многоугольника и его внутренней области.
Верно ли, что многоугольники бывают выпуклые и невыпуклые.
Прямая, проходящая через любую сторону выпуклого многоугольника разделяет его на две части.
Невыпуклый многоугольник находится по одну строну от прямой, проходящей через любую его сторону.
Верно ли, что у многоугольника углов столько же, сколько и сторон.
У четырехугольника и сторон, и углов, и вершин – четыре.
Соседние стороны четырехугольника называют противоположными.
Противоположные вершины четырехугольника не являются соседними.
Четырехугольники бывают только выпуклые.
У четырехугольника можно провести четыре диагонали.
Каждая диагональ разбивает четырехугольник на два треугольника.
Сумма углов любого выпуклого четырехугольника, параллелограмма и трапеции равна 360 0 .
У параллелограмма соседние стороны параллельны и равны.
У параллелограмма противоположные углы равны.
Диагонали параллелограмма точкой пересечения не делятся пополам.
У трапеции противоположные стороны параллельны.
Основания трапеции между собой равны.
Боковые стороны равнобедренной трапеции между собой равны.
У прямоугольной трапеции три угла прямые.
«+» — 3; 4; 6; 9; 10; 11; 14; 15; 17; 20; 21; 23; 27;
«-» — 1; 2; 5; 7; 8; 12; 13; 16; 18; 19; 22; 24; 25; 26; 28
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
За единицу измерения площадей принимают только квадрат со стороной 1 см.
Площадь многоугольника выражается только положительной величиной.
Верно ли, что равные многоугольники имеют равные площади?
Если многоугольник разбит на части, то его площадь равна сумме площадей этих частей.
Площадь квадрата равна кубу его стороны.
Площадь прямоугольника равна половине произведения его противоположных сторон.
Площадь прямоугольника равна произведению его соседних сторон.
Основание – это одна из сторон параллелограмма.
Высота треугольника – это перпендикуляр, опущенный из любой точки противоположной стороны к прямой, содержащей основание.
Площадь параллелограмма равна половине произведения высоты на основание.
Одну из сторон треугольника называют основанием.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если основания двух треугольников равны, то их площади относятся как высоты.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Высота трапеции – это перпендикуляр, проведенный к боковой стороне.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь ромба равна произведению его диагоналей.
Площадь ромба можно найти по той же формуле, что и параллелограмм.
Теорема Пифагора используется в любых треугольниках.
В прямоугольном треугольнике квадрат любого катета равен сумме квадратов гипотенузы и другого катета.
Пифагоровы треугольники те, у которых длины сторон выражаются целыми числами.
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
«+» — 1; 3; 4; 5; 8; 9; 10; 12; 13; 16; 18; 20; 23; 24
«-» — 2; 6; 7; 11; 14; 15; 17; 19; 21; 22;
ТЕМА: «Определение подобных треугольников. Признаки подобия треугольников»
Верно ли, что отношение двух отрезков – это деление одного отрезка на другой?
Если одна пара отрезков пропорциональна другой паре отрезков, то их отношения не равны.
Понятие пропорциональность рассматривается только на примере двух отрезков.
В геометрии фигуры одинаковой формы принято называть подобными.
Если у двух треугольников MNK и M 1 N 1 K 1 соответствующие углы равны, то стороны MK и N 1 K 1 называют сходственными.
Два треугольника называют подобными, если их углы соответственно равны, а стороны одного треугольника соответственно пропорциональны сторонам другого.
Коэффициент подобия – это число, равное отношению сходственных сторон подобных треугольников.
Подобие треугольников нельзя установить, если известно, что некоторые углы соответственно равны или некоторые стороны пропорциональны.
Площади двух подобных треугольников относятся как коэффициент подобия в квадрате.
Отношение периметров двух подобных треугольников равно коэффициенту подобия в квадрате.
По первому признаку подобия треугольников необходимо указать две пропорциональные стороны и угол между ними.
По второму признаку подобия треугольников необходимо указать два равных угла в каждом треугольнике.
По третьему признаку подобия треугольников необходимо указать пропорциональность трех сторон.
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
ТЕМА : «Применение подобия к доказательству теорем и решению задач»
1) Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
2) В любом треугольнике можно провести только одну среднюю линию.
3) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.
4) Средняя линия треугольника отсекает от первоначального треугольника подобный ему треугольник.
5) Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от конца медианы.
6) Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет его на два прямоугольных треугольника не подобных данному треугольнику.
7) Отрезок MN называют средним пропорциональным для двух отрезков АВ и CD, если он равен квадратному корню из суммы этих отрезков.
8) Высота прямоугольного треугольника, проведенная из любой вершины, есть среднее пропорциональное для отрезков, на которые делится катет.
9) Катет прямоугольного треугольника, проведенный из вершины прямого угла, есть среднее пропорциональное для гипотенузы и проекции этого катета на гипотенузу.
10) Метод подобия нельзя применить для решения задач на построение треугольников.
11) Измерительные работы на местности можно провести с помощью подобия двух прямоугольных треугольников.
12) Фигуры F и F 1 называют подобными, если для любых двух точек этих фигур выполняется равенство .
13) Коэффициент подобия – это число, равное отношению сходственных сторон подобных фигур.
14) Верно ли, что если ширина одного прямоугольника больше в 2 раза ширины подобного ему прямоугольника, то длина может быть в 3 раза.
1) Верно ли, что возможны три случая взаимного расположения прямой и окружности.
2) Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность имеют две общих точки.
3) Прямая называется касательной, если расстояние от центра окружности до прямой равно радиусу окружности.
4) По свойству: радиус окружности, проведенный в точку касания перпендикулярен к касательной.
5) Отрезки касательных к окружности, проведенные из одной точки равны.
6) Верно ли, что прямая проходящая через конец диаметра, лежащий на окружности и перпендикулярна к этому диаметру, то она является касательной.
7) На окружности можно построить дугу любой градусной меры.
8) Центральный угол – это угол, одна сторона которого является диаметром.
9) Если центральный угол развернутый, то его соответствующая дуга называется полуокружностью.
10) Если центральный угол больше развернутого, то соответствующая дуга меньше полуокружности.
11) Градусная мера дуги – это градусная мера соответствующего центрального угла.
12) Вписанный угол – это угол, вершиной которого является центр окружности.
13) Говорят, что вписанный угол опирается на дугу, если она не лежит внутри вписанного угла.
14) Вписанный угол равен половине дуги, на которую он опирается.
15) Вписанный угол равен центральному углу.
16) Вписанные углы, опирающиеся на одну и ту же дугу не равны.
17) Вписанный угол, опирающийся на диаметр – прямой.
18) Каждая точка биссектрисы неразвернутого угла находится на разном расстоянии от его сторон.
19) Всего существует четыре замечательных точки треугольника.
20) Вписанная окружность касается всех сторон многоугольника.
21) Все вершины вписанного многоугольника лежат внутри окружности.
22) В любой четырехугольник можно вписать окружность и описать около него окружность.
23) Центры вписанной и описанной окружности треугольника не являются замечательными точками.
«+»: 1; 3; 4; 5; 6; 7; 9; 11; 13; 14; 17; 19; 20;
«-»: 2; 8; 10; 12; 15; 16; 18; 21; 22; 23.
ТЕМА: «Понятие вектора. Сложение и вычитание векторов»
1) Величины, которые задаются не только числовым значением, но и направлением называют векторными величинами.
2) Вектор – это направленный отрезок.
3) У вектора неважно, какая точка является началом, а какая концом.
4) Любую точку можно назвать вектором.
5) Длина вектора – это обязательно расстояние от начала до конца вектора.
6) У нулевого вектора нельзя найти длину.
7) Коллинеарные векторы лежат только на параллельных прямых.
8) Нулевой вектор не может быть коллинеарен произвольному вектору.
9) Коллинеарные векторы делятся на сонаправленные и противоположно направленные.
10) Нулевой вектор имеет любое направление.
11) Векторы называют равными, если их длины равны.
12) От любой точки можно отложить несколько векторов, равных данному.
13) При сложении двух векторов по правилу треугольника необходимо, чтобы начало одного вектора, совпадало с началом другого.
14) При сложении векторов можно пользоваться сочетательным или переместительным законом.
15) При сложении векторов по правилу параллелограмма суммой будет являться диагональ, исходящая из их общего начала.
16) При вычитании векторов результатом будет вектор с началом в конце первого и концом в конце второго.
17) По правилу многоугольника можно сложить любое количество векторов.
18) При сложении по правилу многоугольника все векторы должны иметь общее начало.
«+»: 1; 2; 4; 9; 10; 14; 15; 17
«-»: 3; 5; 6; 7; 8; 11; 12; 13; 16; 18
📸 Видео
Вписанная и описанная окружность - от bezbotvyСкачать

МЕРЗЛЯК-8 ГЕОМЕТРИЯ. ОПИСАННАЯ И ВПИСАННАЯ ОКРУЖНОСТИ ЧЕТЫРЁХУГОЛЬНИКА. ПАРАГРАФ-10. ТЕОРИЯСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

3 правила для вписанного четырехугольника #shortsСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать

СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать

Геометрия 8 класс : Решение задач. Вписанная окружностьСкачать

8 класс - Геометрия - Вписанная и описанная окружностиСкачать









