Видео:Приложение: Успей нажать 🏃 ► C# ► Visual StudioСкачать

Ваш ответ
Видео:Уроки C# / Как сделать первое Windows приложениеСкачать

решение вопроса
Видео:ВЫВОД МАССИВА В ОБРАТНОМ ПОРЯДКЕ C# | РАБОТА С МАССИВАМИ | СИ ШАРП УРОКИ | ДОМАШНИЕ ЗАДАНИЯ # 7Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,989
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Уроки C# .NET Windows Forms / #1 - Создание приложения на C# с SQL (базами данных)Скачать

Индивидуальное задание
Дата добавления: 2015-07-09 ; просмотров: 3591 ; Нарушение авторских прав
1. Напишите приложение, которое строит ряд окружностей. Центр окружностей совпадает с центром экрана. Число окружностей задается при первом вызове рекурсивного метода.
2. Напишите приложение, которое строит ряд квадратов. Центр квадратов совпадает с центром экрана. Число квадратов задается при первом вызове рекурсивного метода.
3. Напишите приложение, которое строит ряд окружностей по диагонали. Число окружностей задается при первом вызове рекурсивного метода.
4. Напишите приложение, которое строит ряд увеличивающихся окружностей по диагонали. Число окружностей задается при первом вызове рекурсивного метода.
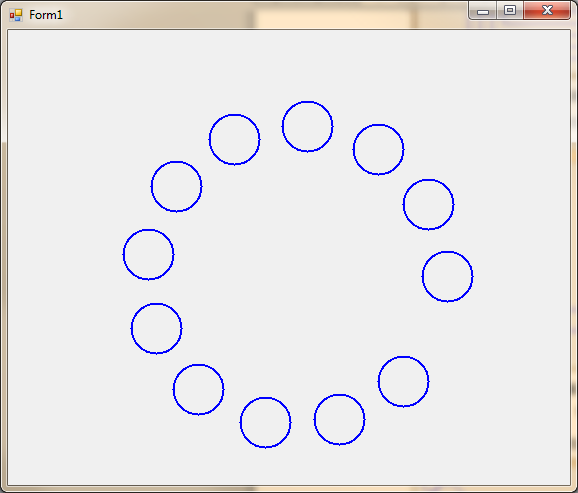
5. Напишите приложение, которое строит ряд окружностей, центры которых лежат на окружности. Число окружностей задается при первом вызове рекурсивного метода.
6. Напишите приложение, которое строит ряд квадратов, центры которых лежат на окружности. Число квадратов задается при первом вызове рекурсивного метода.
7. Напишите приложение, которое строит ряд увеличивающихся окружностей, центры которых лежат на окружности. Число окружностей задается при первом вызове рекурсивного метода.
8. Напишите приложение, которое строит ряд увеличивающихся окружностей, центры которых лежат на спирали. Число окружностей задается при первом вызове рекурсивного метода.
9. Вычислить, используя рекурсию, выражение:
10. Напишите приложение, которое строит ряд окружностей. Число окружностей удваивается на каждом шаге (в рекурсивном методе происходит два рекурсивных вызова). Центры окружностей выбираются каждый раз произвольно (случайно). Линии связывают центры окружностей «предка» и «порожденных» от нее. Число рекурсий задается при первом вызове рекурсивного метода.
11. Напишите приложение, которое строит ряд увеличивающихся окружностей. Число окружностей удваивается на каждом шаге (в рекурсивном методе происходит два рекурсивных вызова). Центры окружностей выбираются каждый раз произвольно (случайно). Толщина линий также увеличивается. Число рекурсий задается при первом вызове рекурсивного метода.
12. Напишите приложение, которое строит ряд уменьшающихся окружностей. Число окружностей удваивается на каждом шаге (в рекурсивном методе происходит два рекурсивных вызова). Число рекурсий задается при первом вызове рекурсивного метода.
13. Напишите приложение, которое строит приведенное ниже изображение. Число рекурсий задается при первом вызове рекурсивного метода. На каждом шаге число окружностей увеличивается в четыре раза (в рекурсивном методе происходит четыре рекурсивных вызова).
14. Постройте ковер Серпинского.
Индивидуальные задания
повышенной сложности
Для решения геометрических задач повышенной сложности необходимо:
1) знать, как представляются на плоскости такие геометрические объекты, как точка, прямая, отрезок и окружность;
2) уметь находить уравнение прямой, соединяющей две заданные точки;
3) уметь определять координаты точки пересечения двух прямых;
4) знать, как провести перпендикуляр к прямой или определить, являются ли прямые параллельными;
5) уметь находить скалярное и векторное произведение;
6) находить площадь многоугольника;
7) уметь работать с фигурами на плоскости.
Напомним основные моменты, связанные с этими понятиями.
Каждую точку плоскости можно считать вектором с началом в точке (0,0). Обозначим через a=(x, y) вектор с координатами (x, y). Длина вектора (его модуль) вычисляется по формуле 
| x |
| y |
| a |
| b |
| φ |
| y1 |
| y2 |
| x1 |
| x2 |
Рис. 16.1. Иллюстрация к скалярному произведению векторов
Скалярное произведение двух векторов – это число, равное произведению модулей этих векторов на косинус угла между ними, (a,b)=|a| ∙ |b| ∙ cos φ. Если вектор a имеет координаты (x1, y1),а вектор b координаты – (x2, y2), то скалярное произведение вычисляется по формуле (a,b)= x1 ∙ x2 + y1 ∙ y2.
Задание 1. Реализуйте задачу «Штраф за левые повороты»
Задача 2 «Здесь будет город-сад». Жители одного дома города Х решили высадить у себя во дворе несколько деревьев. Так как жильцы не смогли договориться, как должны быть расположены посадки, то каждый посадил дерево в том месте двора, где ему захотелось. После проведения посадок полученный сад решили обнести забором. Но пока доски не привезли, деревья обвязали одной длинной веревкой.
Исходная информация: N – количество деревьев в саду, (xi, yi) – координаты деревьев, i=1,2, …, N. Так как были высажены молодые саженцы, то их толщиной можно пренебречь.
Требуется определить, к каким из посаженных деревьев надо привязать веревку так, чтобы все деревья оказались внутри обнесенной зоны, а длина веревки была минимальная.
Эта и подобные ей задачи сводятся к определению для заданного множества точек на плоскости выпуклой оболочки, то есть выпуклого многоугольника с вершинами в некоторых точках из заданного множества, охватывающего все его точки. В [2] приведено несколько вариантов решения такой задачи с учетом временных затрат на выполнение алгоритмов. Здесь мы рассмотрим способ, использующий свойства скалярного произведения векторов.
Будем строить выпуклую оболочку в порядке обхода участка по часовой стрелке. Найдем самую левую точку М0=(x0, y0), x0=min<xi>. Если таких точек несколько, то возьмем самую нижнюю из них. Эта точка наверняка принадлежит искомой выпуклой оболочке. Зададим первоначальный вектор a0 с началом в точке (x0, y0), параллельный оси Oy.
Следующей точкой оболочки будет такая точка М1, чтобы вектор a1 с началом в точке М0 и концом в точке М1 образовывал с первоначальным вектором a0 минимальный угол. Если таких точек несколько, то выбирается точка, расстояние до которой максимально.
Далее процесс продолжаем, то есть ищем точку М2 с минимальным углом между вектором a1 и вектором a2 с началом в точке М1 и концом в точке М2, затем точку М3 и т.д. Процесс прекращаем, когда дойдем до первой выбранной точки или количество точек в оболочке станет равно N.
Для определения угла между векторами используется скалярное произведение. Причем сам угол можно не вычислять, так как минимальному углу соответствует максимальный косинус угла.
Задание 2. Реализуйте задачу «Здесь будет город-сад»
Задача 3 «Заяц» [3]. Недалеко от города Х находится зоосад. Здешний житель, заяц, хаотично прыгая, оставил след в виде замкнутой самопересекающейся ломаной, охватывающей территорию его владения. Найти площадь минимального по площади выпуклого многоугольника, описанного вокруг этой территории.
В данной задаче необходимо не только найти выпуклую оболочку множества точек, но и вычислить площадь выпуклого многоугольника с заданным набором вершин.
Исходные данные: N – количество вершин выпуклого многоугольника, (xi, yi) – координаты вершин, i=1,2, …, N.
Требуется определить площадь выпуклого N-угольника.
Площадь N-угольника может быть вычислена как сумма площадей треугольников, из которых N-угольник составлен. Для нахождения площади треугольника используем векторное произведение. Длина векторного произведения векторов, как известно, равна удвоенной площади треугольника, построенного на этих векторах. Пусть вершины треугольника расположены в точках A=(x1, y1), B=(x2, y2), C=(x3, y3). Совместим начало координат с первой точкой. Векторное произведение равно
[AB × AC]= 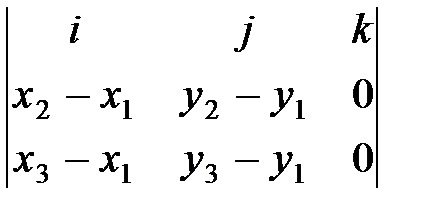
следовательно, площадь треугольника равна
Значение величины SABC может быть как положительным, так и отрицательным числом, так как оно зависит от взаимной ориентации векторов AB и AC, поэтому говорят, что площадь ориентированная.
| А1 |
| А2 |
| А3 |
| А4 |
| А5 |
Для нахождения площади N-угольника последний требуется разбить на треугольники и найти сумму ориентированных площадей этих треугольников. Разбиение N-угольника на треугольники можно провести так: зафиксировать одну из вершин N-угольника, например, первую A1=(x1, y1) и рассматривать все треугольники A1Ai Ai+1, i=2, 3,…, N-1.
Заметим, что аналогичным способом можно находить площадь произвольного многоугольника.
Использование свойства ориентации площади треугольника, вычисленной по векторному произведению, позволяет определить, является ли заданный многоугольник выпуклым. Для выпуклого многоугольника все треугольники, образованные тройками соседних вершин в порядке их обхода, имеют одну ориентацию. Поэтому проверка многоугольника на выпуклость может быть проведена с помощью последовательного сравнения знаков векторных произведений для всех пар соседних сторон многоугольника.
Задание 3. Реализуйте задачу «Заяц»
Задача 4 «Тигр в загоне». Недалеко от города Х находится заповедник, в котором обитают уссурийские тигры. Работники заповедника очень переживают, когда тигр покидает охраняемую зону. Программа охраны уссурийских тигров предусматривает снабжение каждого тигра ошейником с радиомаяком. Сигнал от тигриного радиомаяка поступает в центр охраны и позволяет определить местоположения тигра. Территория заповедника представляет собой произвольный многоугольник.
Исходные данные: N – количество вершин многоугольника, задающего заповедник, (xi, yi) – координаты его вершин, i=1,2, …, N. (X, Y) – координаты точки, в которой находится тигр.
Требуется определить, находится ли тигр на территории заповедника, или надо срочно снаряжать спасательную экспедицию.
| P |
| Q |
Очень часто при решении задач геометрического содержания требуется проверить, лежит ли заданная точка внутри или вне многоугольника. Таким способом можно решить, например, задачу о Бармаглоте, проверяя каждую точку Бармаглота относительно одеяла-многоугольника. Есть много способов проверки принадлежности точки многоугольнику, однако мы приведем здесь один из них, основанный на использовании произведения векторов.
Идея метода заключается в том, чтобы определить сумму углов, под которыми стороны многоугольника видны из проверяемой точки. Если точка лежит внутри многоугольника, то суммарный угол равен 2π (точка Р на рисунке), если же точка лежит вне многоугольника, то сумма углов не равна 2π (точка Q).
Таким образом, для решения надо перебрать в цикле последовательно все вершины многоугольника и найти сумму углов между векторами PAi и PAi+1, i=1,2, …, N. Не забудьте добавить угол между векторами PAN и PA1. Для определения величины угла между векторами нам потребуется формула скалярного произведения.
Так как стороны многоугольника должны рассматриваться последовательно, в порядке обхода вершин, то при нахождении суммарного угла следует учитывать взаимное расположение векторов. Угол, под которым сторона видна из исследуемой точки, может быть как положительным, так и отрицательным. Для определения знака угла воспользуемся векторным произведением. Знак векторного произведения и определит знак конкретного угла в общей сумме.
Задание 4. Реализуйте задачу «Тигр в загоне»
Задача 5 «Пересечение отрезков». Дано n отрезков. Реализовать программу, находящую все их пересечения между собой. Отобразить решение графически.
На плоскости заданы два отрезка a и b, a – точками A 1 (A 1 x,A 1 y) и A 2 (A 2 x,A 2 y), а b – точками B 1 (B 1 x,B 1 y) и B 2 (B 2 x,B 2 y). Найти и напечатать возможную точку их пересечения C(Cx,Cy). Рассмотрим первый отрезок a. Уравнение прямой, на которой он лежит можно записать так:
Здесь, A 1 x,A 1 y,A 2 x,A 2 y – константы, xa,ya – точки принадлежащие отрезку, при ta изменяющемся от 0 до 1. Аналогично для отрезка b:
Таким образом, приравнивая соответствующие координаты, получаем задачу нахождения параметров ta,tb, при которых бы выполнялись равенства:
После разрешения системы относительно ta,tb получаем:
А это есть система из двух линейных уравнений относительно ta,tb.
Видео:Решение квадратного уравнения на C# для Windows Forms в Visual Studio 2022Скачать

Используем в рисовании переменные величины
Если вы нарисовали снеговика, то наверное согласитесь, что для этого вам пришлось основательно потрудиться, хотя сам рисунок не слишком богат, в нем всего порядка десяти элементов.
Как заставить Паскаль короткой программой рисовать множество элементов? Ответ: применять циклы, используя в обращениях к графическим процедурам вместо чисел переменные величины и арифметические выражения.
Задача: Нарисовать горизонтальный ряд окружностей радиусом 10 на расстоянии 100 от верхнего края экрана и с такими горизонтальными координатами 50, 80, 110, 140, , 290.
Как видим, центры соседних окружностей отстоят друг от друга на 30. Вот примитивный фрагмент, решающий эту задачу:
При вводе этой программы вас будет раздражать необходимость вводить много раз почти одно и то же. Воспользуйтесь копированием, которое объяснено в параграфе «Копирование и перемещение фрагментов текста» из части IV.
Мы видим, что здесь Паскаль 9 раз выполнит одну и ту же процедуру, причем при каждом следующем обращении первый параметр вырастает на 30.
А теперь решим эту же задачу при помощи цикла.
Придумаем для первого параметра переменную величину, например, х. Чтобы х изменялся, организуем цикл repeat. Вот программа решения задачи:
VAR x, Device, Mode :Integer;
Задание 69:. Попробуйте уменьшить расстояние между центрами окружностей, не изменяя их радиуса, нарисовав их плотнее, чтобы они пересекались, еще плотнее, пока они не образуют “трубу”.
Задание 70:. Удлините трубу налево и направо до краев экрана.
Задание 71:. Увеличьте толщину трубы.
Заставим окружности вести себя посложнее. Например, расположим их не по горизонтали, а по диагонали экрана в направлении от левого верхнего угла в правый нижний. Для этого организуем еще одну переменную — вертикальную координату у — и заставим ее тоже изменяться одновременно с x.
VAR x, y, Device, Mode : Integer;
Если мы захотим менять радиус, то организуем переменную R, тоже типа Integer.
Задание 72:. Нарисуйте ряд точек по направлению из левого нижнего угла в правый верхний.
Задание 73:. “Круги на воде”. Нарисуйте пару десятков концентрических окружностей, то есть окружностей разного радиуса, но имеющих общий центр.
Задание 74:. “Компакт-диск”. Если радиус самого маленького “круга на воде” будет порядка 50, а самого большого — во весь экран, и если радиусы соседних окружностей будут различаться на 2-3 пиксела, то на экране вы увидете привлекательный “компакт-диск”. Сделайте его золотым (Yellow).
Задание 75:. Не трогая x, а меняя только y и R, вы получите коническую башню.
Задание 76:. Меняя все три параметра, вы получите трубу, уходящую в бесконечность.
Задание 77:. Разлинуйте экран в линейку.
Задание 78:. А теперь в клетку.
Задание 79:. А теперь в косую линейку.
Задание 80:. Начертите ряд квадратов.
Чтобы получить богатые рисунки, нужно использовать богатые возможности Паскаля: вложенные циклы, ветвление внутри цикла и т.д., например:
Задание 81:. Нарисуйте шахматную доску.
Задание 82:. “Ковер”. В задании 69 вы рисовали горизонтальный ряд пересекающихся окружностей. Теперь нарисуйте один под другим много таких рядов.
Указания: Здесь вам понадобятся вложенные циклы. Если центры соседних окружностей отстоят друг от друга на одинаковое расстояние что по горизонтали, что по вертикали, и если удачно подобраны остальные числа, то у вас получится красивый ковер во весь экран с аккуратными краями.
Задание 83:. Пусть у этого ковра будет вырезан левый нижний угол.
Задание 84:. и вдобавок вырезан квадрат посередине.
📹 Видео
C# .NET Windows Form | СОЗДАЁМ PAINT НА C#Скачать

Как создать калькулятор на C#. Простое приложение для начинающий программистовСкачать

Приложение: Шашки 🤔 ► часть 2 ► C#Скачать

ПРЕДСКАЗЫВАЮ БУДУЩЕЕ НА C# | СОЗДАНИЕ ДЕСКТОПНОГО ПРИЛОЖЕНИЯ НА C# | WINDOWS FORMS | ASYNC AWAIT C#Скачать

Консольное приложение - игра в загаданное число в C#Скачать

Уроки C# – WinAPI + свой контрол (2 в 1)Скачать

Решение квадратного уравнения на C# для консоли Windows в Visual Studio 2022Скачать

Приложение "Напоминалка" на Windows FormsСкачать

C# Урок 3. Работа с компонентами Textbox Label Button.Скачать

Пишем десктопное приложение на пяти языках / программа на C#Скачать

создание блокнота на windows forms c#Скачать

Уроки C# / Как обработать ошибкуСкачать
ОКОННОЕ ПРИЛОЖЕНИЕ С НУЛЯ - ПОЛНЫЙ БАЗОВЫЙ КУРС C++ WINAPIСкачать