 Школе NET
Школе NET - Register
- Login
- Newsletter
- Пармезан Черница
- найдите площадь выпуклого четырехугольника с диагоналями 8 и 5, если отрезки, соединяющие середины его протиаолежащих сторон, равны
- Репетитор по математике
- Стоимость занятий
- Видеокурсы подготовки к ЕГЭ-2021
- Группа Вконтакте
- Преимущества
- Педагогический стаж
- Собственная методика
- Гарантированный результат
- Индивидуальная работа
- Презентация к открытому уроку по геометрии «Выпуклые четырёхугольники . Специфика параллелограммов . Специфика трапеций» презентация к уроку по геометрии (9 класс) по теме
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- По теме: методические разработки, презентации и конспекты
- 🔥 Видео
Register
Do you already have an account? Login
Login
Don’t you have an account yet? Register
Newsletter
Submit to our newsletter to receive exclusive stories delivered to you inbox!
- Главная
- Вопросы & Ответы
- Вопрос 14274801
Пармезан Черница
Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольникаСкачать

найдите площадь выпуклого четырехугольника с диагоналями 8 и 5, если отрезки, соединяющие середины его протиаолежащих сторон, равны
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Репетитор по математике
Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».
Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
Стоимость занятий
Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.
Видеокурсы подготовки к ЕГЭ-2021
Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.
Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.
Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Группа Вконтакте
В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Видео:ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Преимущества
Педагогический стаж
Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.
Собственная методика
За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.
Гарантированный результат
За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.
Индивидуальная работа
Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Презентация к открытому уроку по геометрии «Выпуклые четырёхугольники . Специфика параллелограммов . Специфика трапеций»
презентация к уроку по геометрии (9 класс) по теме
Презентация содержит слайды с заданиями и решением задач к уроку по геометрии в 9 классе » Выпуклые четырёхугольники
Специфика параллелограммов Специфика трапеций «
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| zadanie_k_otkrytomu_uroku.pptx | 499.64 КБ |
Предварительный просмотр:
Видео:Диагонали четырехугольника равны 4 и 5.Скачать

Подписи к слайдам:
ГОСУДАРСТВЕННАЯ ИТОГОВАЯ АТТЕСТАЦИЯ ОСНОВНОЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН МАТЕМАТИКА 9 КЛАСС МОДУЛЬ ГЕОМЕТРИЯ (часть 2) Выпуклые четырёхугольники Специфика параллелограммов Специфика трапеций Учитель математики высшей категории Сысуева Ольга Александровна, ГБОУ СОШ№ 22 г.о . Чапаевск, Самарской области
Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними: O d 1 d 2 α
O d 1 d 2 α S 1 S 2 S 3 S 4 Диагонали выпуклого четырёхугольника делят его на части так, что произведения площадей треугольников, прилегающих к противоположным сторонам четырёхугольника, равны : Обоснование : найти площадь каждого из образованных диагоналями четырёх треугольников по формуле Затем сложить эти площади (свойство 1) или перемножить ( свойство 2).
Середины сторон выпуклого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади данного четырёхугольника.
C D B A s s s s o Диагонали параллелограмма делят его на две пары равных треугольников; площади всех этих треугольников равны между собой. Специфика параллелограмма
C D B A b a o a b d 1 d 2 В параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его c торон : d 1 2 + d 2 2 = 2(a 2 +b 2 ) Специфика параллелограмма
Специфика параллелограмма 3 . Биссектрисы углов, прилежащих к любой из сторон параллелограмма, перпендикулярны . C D B A
Специфика параллелограмма C D B A При проведении биссектрисы любого угла параллелограмма получается равнобедренный треугольник.
Специфика параллелограмма C D B A Параллелограмм, у которого все стороны равны, является ромбом. Параллелограмм, диагонали которого взаимно перпендикулярны, является ромбом. 3 . Параллелограмм, диагонали которого являются биссектрисами его углов, является ромбом.
C D B A Специфика параллелограмма C D B A 5 . Параллелограмм, диагонали которого равны, является прямоугольником. 6. Параллелограмм , диагонали которого взаимно перпендикулярны и равны, является квадратом. C D B A Параллелограмм, имеющий равные высоты, является ромбом.
C D B A s s 1 s s 2 o Специфика трапеций Диагонали трапеции, пересекаясь, образуют четыре треугольника, два из которых равновелики, а два других – подобны с коэффициентом подобия равным отношению оснований трапеции. OAD
OCB (по двум равным углам), S OAD : S OCB = k 2 , где k = AD : BC = OA : OC = OD : OB .
C D B A s s 1 s s 2 o Специфика трапеций 2. S BAD = S CAD , S ABC = S DBC (как площади треугольников, имеющих c оответственно одинаковые основания и высоты). 3. S OAB = S OCD (т.к. S OAB = S ABC – S OBC = S DBC – S OBC = S OCD ) . 4. S BAD : S DBC = AD : BC ( S BAD = 0 ,5 · AD·h , S DBC = 0 ,5 · BC·h ) .
C D B A s s 1 s s 2 o Специфика трапеций 5. Диагонали трапеции делят её на четыре треугольника так, что произведение площадей тех из них, которые прилежат к основаниям, равно квадрату площади треугольника, прилежащего к любой из боковых сторон трапеции: S 1 S 2 = S 2 . ( S OAD = S 1 =0 , 5·OB·OC·sin α , S OCB = S 2 =0 , 5·OA·OD·sin α , S OAB = S=0 , 5·OA·OB·sin(180° – α )=0 , 5·OA·OB·sin α , S OCD = S=0 , 5·OC·OD·sin(180° – α )=0 , 5·OA·OB·sin α , тогда S 1 S 2 = S 2 ) .
6 . Биссектрисы углов, прилежащих к боковым сторонам трапеции, перпендикулярны (следует из того факта, что сумма этих углов равна 180° как сумма односторонних углов при параллельных прямых и секущей). C D B A C D B A o 7. Точка пересечения диагоналей, точка пересечения продолжений боковых сторон, середина верхнего и середина нижнего основания – лежат на одной прямой. Специфика трапеций
Специфика трапеций Основные (наиболее распространённые) дополнительные построения в задачах на трапецию. C D B A Построение 1 Через вершину меньшего основания трапеции провести прямую, параллельную её боковой стороне, до пересечения со вторым основанием; трапеция разбивается на параллелограмм и треугольник.
Специфика трапеций Основные (наиболее распространённые) дополнительные построения в задачах на трапецию C D B A E Построение 2 Из вершины С меньшего основания трапеции ABCD провести прямую CE , параллельную диагонали BD , до пересечения с AD в точке E ; получится треугольник ACE , две стороны которого равны диагоналям трапеции, а длина третьей равна сумме длин оснований трапеции AE = AD + DE . При этом площадь трапеции ABCD равна площади образованного треугольника ACE : S ABCD = S ACE
Специфика трапеций Основные (наиболее распространённые) дополнительные построения в задачах на трапецию C D B A H 1 H 2 C D B A P Построение 4 Достроить трапецию ABCD до треугольника APD , вершина Р которого образуется при пересечении продолжений боковых сторон трапеции. Построение 3 Из вершин меньшего основания трапеции опустить две высоты BH 1 и CH 2 .
Задача №1. (Тренировочные варианты Иркутск 2013г.) Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины противоположных сторон равны. O A D C B K P T H
Решение . Точки K , Р , Т , Н середины сторон четырёхугольника ABCD. Отрезки АС и В D – диагонали четырёхугольника ABCD . O A D C B K P T H По условию КТ = РН ; значит, параллелограмм КРТН – прямоугольник, угол КРТ – прямой; следовательно, угол между диагоналями В D и АС тоже прямой, а значит, S ABCD = 0 ,5· В D· АС = 0 ,5 · 3 · 4 = 6. Ответ: 6. 2 . По свойству средней линии треугольника отрезки КН и РТ параллельны диагонали В D и равны её половине; отрезки КР и НТ параллельны диагонали АС и равны её половине. Значит, КРТН – параллелограмм .
Задача №2. (ФИПИ 2014г.) На стороне В C параллелограмма ABCD выбрана точка К. Отрезки АК и В D пересекаются в точке Р . Площадь параллелограмма ABCD равна 24, а площадь четырёхугольника РКС D равна 10. Найдите площадь треугольника АР D . C D B A K P
C D B A K P Решение . A В D = CDB (по трём равным сторонам). S A В D = S CDB = 0 ,5· S A В CD = =0,5·24=12; S КР B = S CDB – S PKCD = 12 – 10 = 2 2 . APD
KPB (по двум равным углам); S A Р D : S KPB = k 2 ; AP= k·PK , DP= k·PB 3 . A В P и В PK имеют общую высоту из вершины В , значит, отношение их площадей равно отношению их оснований, т.е. S A В P : S KPB = А P : PK = k (из п.2 ) 4 . APD и ABP имеют общую высоту из вершины A , значит, отношение их площадей равно отношению их оснований, т.е. S AP D : S A В P = DP : PB = k (из п.2 )
C D B A K P 5. Из п.3 и п.1 S A В P = k·S KPB = 2k 6. Из п.4 и п. 5 S APD = k·S ABP = k·2k = 2 k 2 S ABD = S A В P + S APD = 2k + 2 k 2 . Из п. 1 следует 2k + 2 k 2 = 12. Корни уравнения k 2 + k – 6 = 0 числа – 3 и 2; по смыслу задачи k = 2 . 8. S APD = 2 k 2 = 2·2 2 = 8 . Ответ: 8 .
C D B A s s 1 s s 2 o Задача №3. (МИОО 2013г.) Диагонали AC и BD трапеции ABCD пересекаются в точке О . Площади треугольников O А D и OC В равны соответственно 16 см 2 и 9 см 2 . Найдите площадь трапеции.
C D B A s s 1 s s 2 o A ВО и СВО имеют общую высоту из вершины В , значит, отношение их площадей равно отношению их оснований, т.е. S A ВО : S C ВО = ОА : О C = 4:3 (из п.2 ). Следовательно, S A ВО = Решение . По условию S OAD не равна S OCB , значит, AD и BC – основания трапеции ABCD . 2. OAD
OCB (по двум равным углам ), S OAD : S OCB = k 2 =16:9, где k = 4:3 = OA : OC .
C D B A s s 1 s s 2 o 4. S BAD = S CAD , т. к. эти треугольники имеют общее основание AD и их высоты, проведённые к этому основанию, равны как высоты трапеции. Значит, S OAB = S ABC – S OBC = S DBC – S OBC = S OCD , т. е. S OCD = S OAB = 12 . 5. S A В CD = S OAD + S OCB + S OCD + S OAB = 16 + 9 + 12 +12 = 49 c м 2 . Ответ: 49 c м 2 .
K P N A o M B Задача №4. (МИОО 201 0 г.) Прямая, параллельная основаниям MP и NK трапеции MNKP , проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны MN и KP в точках A и B соответственно. Найдите длину отрезка AB , если MP =40 см, NK =24 см.
K P N A o M B 2. Δ AMO
Δ NMK по двум углам: а) ∠ М общий; б) ∠ MAO = ∠ MNK как соответственные при AO параллельной NK и секущей MN . Решение . Δ MOP
Δ KON по двум углам: а ) ∠NOK=∠MOP как вертикальные б ) ∠PMO=∠NKO как внутренние накрест лежащие углы при NK параллельной MP и секущей MK.
K P N A o M B 3. Аналогично 4. AB = 30 см . Ответ: 30 см.
Задача №5. (МИОО 2013г.) В трапеции ABCD на диагонали BD выбрана точка Е так, что Площадь треугольника DCB равна 15. Найдите площадь треугольника А B Е. C D B A F E
Решение . 1 . Пусть точка F – точка пересечения прямых CE и AD . Тогда ABCF – параллелограмм (по определению параллелограмма ). BF – диагональ параллелограмма делит его на два равных треугольника; S FCB = 0 ,5· S ABCF C D B A F E
3. A В E и параллелограмм ABCF имеют одно и то же основание AB и общую высоту, проведённую к AB . Значит, S АВЕ = 0 ,5· S ABCF = S DCB = 15. Ответ: 15. C D B A F E 2. S DCB = S FCB ( как площади треугольников, имеющих общее основание и одинаковую высоту – высоту трапеции ) . Значит, S DCB = S FCB = 0 ,5· S ABCF = 15.
Задача № 6 (МИОО 2013г.) В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC . К диагоналям трапеции провели перпендикуляры BH и CE . Найдите площадь четырёхугольника BCEH , если площадь трапеции ABCD равна 36. D A B N C M H E
D A B N C M H E Решение . По свойству равнобедренной трапеции AC=BD , следовательно, треугольники ABC и DCB равны. Так как AB=BC=CD , треугольники ABC и DCB равнобедренные, следовательно, BH и CE – соответствующие медианы этих треугольников. Значит, AH=HC=BE=ED . Отрезок HE соединяет середины диагоналей трапеции, c ледовательно , прямые HE, AD и BC параллельны, поэтому, BCEH – трапеция.
D A B N C M H E Площадь трапеции ABCD : Ответ: 9 .
Задача № 7 . Диагонали трапеции 3 и 5; отрезок, соединяющий середины оснований 2. Найдите площадь трапеции. C D B A F K L M Решение . 1 . Дополнительное построение: СМ параллельна KL , CF параллельна BD . 2. Из построения следует: LKCM и DBCF параллелограммы; LM = KC = 0,5· BC , DF = BC , AM = AL+LM = 0,5· AD + 0,5· BC. 3. CM – медиана треугольника ACF. По формуле медианы
C D B A F K L M Пусть h – высота трапеции ABCD или треугольника ACF . Тогда S ABCD = 0 , 5· ( AD+BC ) ·h = 0 , 5· ( AD+DF ) ·h = 0 , 5·AF·h = S ACF =6. Ответ: 6 . По формуле Герона Полупериметр треугольника ACF равен
1. Найдите площадь выпуклого четырёхугольника с диагоналями 8 и 5, если отрезки, соединяющие середины противоположных сторон равны. 2. В выпуклом четырёхугольнике ABC Т длина отрезка , соединяющего середины сторон AB и C Т, равна одному метру . Прямые B Т и AC перпендикулярны. Найдите длину отрезка , соединяющего середины диагоналей AC и B Т. 3. На стороне В C параллелограмма ABCD выбрана точка К. Отрезки АК и В D пересекаются в точке Р . Площадь параллелограмма ABCD равна 80, а площадь четырёхугольника РКС D равна 31. Найдите площадь треугольника АР D . Зад а чи для самостоятельного решения Ответ: 20. Ответ: 1 метр . Ответ: 25.
4. Диагонали AC и BD трапеции ABCD пересекаются в точке О . Площади треугольников А OD и В OC равны соответственно 25 см 2 и 16 см 2 . Найдите площадь трапеции. 5. Прямая, параллельная основаниям BC и AD трапеции ABCD , проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны AB и CD в точках Е и F соответственно. Найдите длину отрезка Е F , если AD= = 12 см, В C =24 см. 6. В трапеции ABCD ( AD параллельна BC , AD > BC ) на диагонали AC выбрана точка Е так, что ВЕ параллельна CD . Площадь треугольника АВ C равна 10. Найдите площадь треугольника D Е C . Задачи для самостоятельного решения Ответ: 81 см 2 . Ответ: 16 см. Ответ: 10.
А.С. Зеленский , И.И. Панфилов «Геометрия в задачах». Учебное пособие для учащихся старших классов и поступающих в вузы. – Москва, НТЦ «Университетский» УНИВЕР-ПРЕСС, 2008. И.В. Ященко, С.А. Шестаков и др. Математика. 9 класс. Типовые тестовые задания. – «Экзамен», Москва, 2013. Образовательный портал для подготовки к экзаменам РЕШУ ЕГЭ http://pedsovet.su/load/321 http://www.mathvaz.ru/ http://alexlarin.net/ Использованные источники
Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

По теме: методические разработки, презентации и конспекты
Презентация Площадь параллелограмма, треугольника, трапеции
Презентация подготовлена к уроку геометрии в 8 классе по теме «Площади четырёхугольников». Урок проводился в математическом классе и успели разобрать весь материал, представленный в презентации. После.
Презентация к уроку геометрии по теме «Площадь параллелограмма»
Урок изучения нового материала с использованием слайдовой презентации и видеоролика с доказательством теоремы о площади параллелограма.
Презентация к уроку геометрии в 8 классе по теме: «Параллелограмм и трапеция»
На готовых чертежах можно показать прилежащие и противолежащие стороны и углы; найти их величину, используя свойства фигур. Можно использовать презентацию как при объяснении, так и при повторении мате.
Бинарный урок по геометрии и информатике «Параллелограмм и трапеция»
Урок-обобщение по геометрии «Параллелограмм и тапеция» с использованием ПК и интерактивной доски для 8 класса.
Презентация к уроку «Площадь параллелограмма, треугольника, трапеции»
Презентация содержит материал для повторения и подготовки к ГИА. В ней представлены задачи диагностических работ прошлых лет по данной теме.
Презентация к уроку по геометрии в 8 классе «Площадь трапеции»
Геометрия – древняя наука, она и возникла на основе практической деятельности людей и служила преимущественно практическим целям. Мы много изучаем теоретический материал для то.
Презентация к уроку геометрия 8 класс : » Площадь параллелограмма»
Презентация к уроку геометрия 8 класс : » Площадь параллелограмма".
🔥 Видео
Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

ОГЭ без рекламы математика 11 и 12 вариант задача 25Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Найти площадь закрашенного четырехугольника. Произвольный четырехугольникСкачать

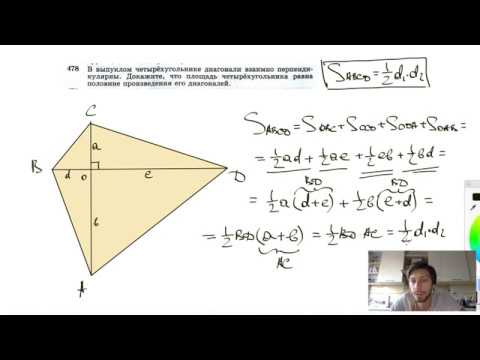
№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать
Геометрия Найдите площадь выпуклого четырехугольника диагонали которого равны 3√3 см и 4 см а уголСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Как найти периметр данной фигуры? Решение за одну минуту!Скачать

Геометрия Диагонали выпуклого четырехугольника равны 8 см и 12 см а угол между ними 30 НайдитеСкачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать










