- Разделы
- Дополнительно
- Задача по математике — 4921
- Задача по математике — 4922
- Задача по математике — 4923
- Задача по математике — 4924
- Задача по математике — 4925
- Задача по математике — 4926
- Задача по математике — 4927
- Задача по математике — 4928
- Задача по математике — 4929
- Задача по математике — 4930
- Задача по математике — 4931
- Задача по математике — 4932
- Задача по математике — 4933
- Задача по математике — 4934
- Задача по математике — 4935
- Четырёхугольник
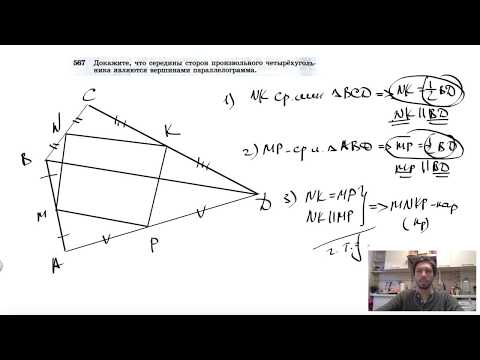
- Точки P, Q, R и T на рисунке 86 — середины сторон четырехугольника ABCD. Докажите, что четырехугольник PQRT — параллелограмм.
- Ваш ответ
- Похожие вопросы
- 🎦 Видео
Видео:№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
Разделы 
Видео:Теорема Вариньона. Середины сторон четырёхугольника.Скачать
Дополнительно
Задача по математике — 4921
В выпуклом четырёхугольнике $ABCD$ точки $E$, $F$, $H$, $G$ являются соответственно серединами отрезков $AB$, $BC$, $CD$, $AD$; $O$ — точка пересечения отрезков $EH$ и $FG$. Известно, что $EH=a$, $FG=b$, $angle FOH=60^$. Найдите диагонали четырёхугольника $ABCD$.
Задача по математике — 4922
Докажите, что если отрезки, соединяющие середины противоположных сторон четырёхугольника,
а) равны, то диагонали четырёхугольника перпендикулярны;
б) перпендикулярны, то диагонали четырёхугольника равны.
Задача по математике — 4923
Докажите, что четыре отрезка, каждый из которых соединяет вершину четырёхугольника с точкой пересечения медиан треугольника, образованного тремя оставшимися вершинами, пересекаются в одной точке и делятся ею в отношении $3:1$, причём эта точка — середина отрезка, соединяющего середины противоположных сторон четырёхугольника.
Задача по математике — 4924
Радиусы $OA$ и $OB$ высекают на окружности с центром $O$ дугу величиной $60^$. На этой дуге взята точка $M$. Докажите, что прямая, проходящая через середины отрезков $MA$ и $OB$, перпендикулярна прямой, проходящей через середины отрезков $MB$ и $OA$.
Задача по математике — 4925
Параллелограмм с периметром, равным 44, разделён диагоналями на четыре треугольника. Разность между периметрами двух смежных треугольников равна 6. Найдите стороны параллелограмма.
Задача по математике — 4926
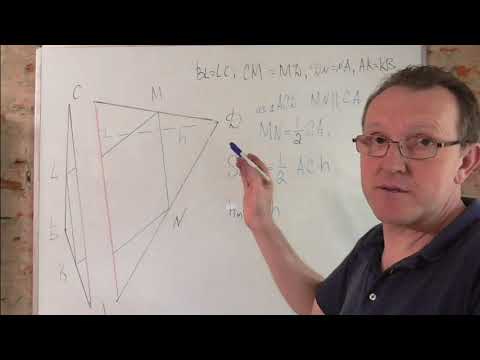
Внутри треугольника $ABC$ взята произвольная точка $O$ и построены точки $A_$, $B_$ и $C_$, симметричные точке $O$ относительно середин сторон $BC$, $CA$ и $AB$. Докажите, что треугольники $ABC$ и $A_B_C_$ равны, а прямые $AA_$, $BB_$ и $CC_$ пересекаются в одной точке.
Задача по математике — 4927
Дана трапеция $ABCD$ с основанием $AD$. Биссектрисы внешних углов при вершинах $A$ и $B$ пересекаются в точке $P$, а при вершинах $C$ и $D$ — в точке $Q$. Докажите, что длина отрезка $PQ$ равна полупериметру трапеции.
Задача по математике — 4928
В равнобедренном треугольнике $ABC$ с основанием $AC$ проведена биссектриса $CD$. Прямая, проходящая через точку $D$ перпендикулярно $DC$, пересекает $AC$ в точке $E$. Докажите, что $EC=2AD$.
Задача по математике — 4929
Площадь равнобедренной трапеции равна 32. Котангенс угла между диагональю и основанием равен 2. Найдите высоту трапеции.
Задача по математике — 4930
Периметр треугольника равен 28, середины сторон соединены отрезками. Найдите периметр полученного треугольника.
Задача по математике — 4931
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Найдите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна 12.
Задача по математике — 4932
Диагонали выпуклого четырёхугольника $ABCD$ взаимно перпендикулярны. Через середины сторон $AB$ и $AD$ проведены прямые, перпендикулярные противоположным сторонам $CD$ и $CB$ соответственно. Докажите, что эти прямые и прямая $AC$ имеют общую точку.
Задача по математике — 4933
Докажите, что биссектрисы углов при боковой стороне трапеции пересекаются на средней линии.
Задача по математике — 4934
Пусть $P$ и $Q$ — середины сторон $AB$ и $CD$ четырёхугольника $ABCD$, $M$ и $N$ — середины диагоналей $AC$ и $BD$. Докажите, что если $MN$ и $PQ$ перпендикулярны, то $BC=AD$.
Задача по математике — 4935
В прямоугольнике $ABCD$ точка $M$ — середина стороны $BC$, точка $N$ — середина стороны $CD$, $P$ — точка пересечения отрезков $DM$ и $BN$. Докажите, что угол $MAN$ равен углу $BPM$.
Видео:№43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать

Четырёхугольник
В школьном курсе геометрии изучаются только отдельные виды четырёхугольников.
Теорема 1 (Вариньона). Середины сторон произвольного четырехугольника являются вершинами параллелограмма, стороны которого параллельны диагоналям четырёхугольника и равны их половинам.
Доказательство. 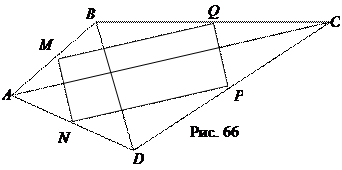

Аналогично получим, что
NP || АС || MQ, NP = 
Теорема 2. Около четырёхугольника, образованного биссектрисами углов данного выпуклого четырёхугольника, можно описать окружность.

четырёхугольника АВСD образуют четырёхугольник
Докажем, что Ð Q + Ð S = 180°. Действительно,
Ð Q + Ð S = 180° – (Ð QAD + Ð QDA) + 180° –
– (Ð SBC + Ð SCB) = 360° – 
+Ð ABC + Ð DCB) = 360° – 
Теорема 3 (Бретшнайдера). Квадрат произведения диагоналей четырехугольника равен сумме квадратов произведений его противолежащих сторон без удвоенного произведения всех его сторон на косинус суммы двух противолежащих углов.

Ð ADМ = Ð BAС, Ð DАМ = Ð BСА, а Ð КАВ = Ð AСD, Ð КВА = Ð САD и Ð КАМ = Ð BAD + Ð BСD.
Тогда D АDМ 

Значит, 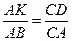
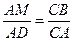
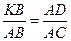
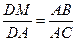
Тогда АК = 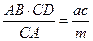
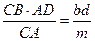
КВ = 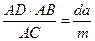
Поскольку Ð КBD + Ð BDМ = (Ð КВА + Ð АBD) +
= Ð АBD + Ð BDА + Ð BAD = 180°, то ВК || DМ и четырехугольник ВDМК параллелограмм.
Поэтому КМ = ВD = n. По теореме косинусовприменённой к треугольнику АКМ, получим
КМ 2 = АК 2 + АМ 2 – 2 Ак АМ cos Ð KAM, или
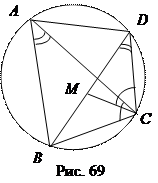
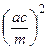
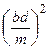
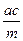
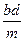
Теорема 4 (Птолемея). Произведение диагоналей вписанного в круг четырёхугольника равно сумме произведений противоположных сторон.
Доказательство. Пусть четырёхугольник АВСD вписан в окружность (рис. 69). На диагонали ВD возьмем точку М так, что Ð МСD = Ð ВСА. Тогда, учитывая, что Ð ВАС = Ð ВDС, получим D АВС 
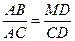
Из подобия D САD 
Ð АСD = Ð DСМ – Ð АСМ = Ð АСВ – Ð АСМ = Ð МСВ) получим 
Из полученных пропорций находим
АВ СD = АС МD и ВС АD = АС МВ, откуда
АВ СD + ВС АD = АС (МD + ВМ) = АС ВD.
Отметим, что теорему Птолемея можно получить в качестве непосредственного следствия из теоремы Бретшнайдера. Действительно, для вписанного в круг четырёхугольника Ð А + Ð С = 180°, поэтому
Теорема 5. Если произведение диагоналей четырёхугольника равно сумме произведений его противолежащих сторон, то около этого четырёхугольника можно описать окружность.
Доказательство. Пусть a, b, c, d – длины последовательных сторон четырёхугольника, m и n – длины его диагоналей, А и С противолежащие углы. Пусть так же mn = aс + bd. Тогда m 2 n 2 = a 2 c 2 + b 2 d 2 + 2 abcd.
По теореме Бретшнайдера имеем
Сравнив равенства, получим cos (Ð A + Ð C) = –1, откуда Ð A + Ð C = 180º.
Следствие 1. В любом четырёхугольнике произведение его диагоналей не превышает суммы произведений его противолежащих сторон и больше разности этих произведений.
Действительно, по теореме Бретшнайдера
Поскольку –1 2 c 2 + b 2 d 2 – 2 abcd 2 n 2 2 c 2 + b 2 d 2 + 2 abcd,
Отметим, что если прямую рассматривать как окружность бесконечно большого радиуса, то следствие 2 можно рассматривать как частный случай теоремы Птолемея.
Задача 1 (Теорема Помпея). Доказать, что отрезки, соединяющие произвольную точку М плоскости с вершинами правильного треугольника, могут служить сторонами треугольника АВС, если точка М не принадлежит описанной около треугольника АВС окружности. Найти угол треугольника, образованного отрезками АМ, ВМ и СМ, противолежащий стороне ВМ, если Ð АМС = a.

– 2 АВ ВС СМ МА cos (60º + Ð АМС).
Учтя, что АВ = ВС = СА, будем иметь
ВМ 2 = МС 2 + АМ 2 – 2 СМ МА cos (60º + Ð АМС).(1)
Поскольку точка М не принадлежит описанной около треугольника АВС окружности, то Ð АМС = 120º. Кроме того, 60º + Ð АМС > 0º. Поэтому
–1 2 + АМ 2 – 2 СМ МА 2 2 + АМ 2 + 2 СМ МА,
или (MC – MA) 2 2 2 , или |MC – MA| 2 = 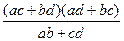
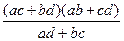
х1 = 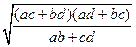
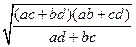
Для случая (a, c, b, d) аналогично получим:
х2 = 
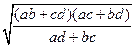
Наконец, для случая (a, b, d, c) будем иметь:
х3 = 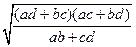
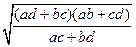
Теорема 7.Если четырёхугольник АВСD описан около круга, то суммы противолежащих его сторон равны: АВ + СD = АD + ВС.

Поскольку касательные к кругу, проведённые из одной точки, равны, то АМ = АQ, BM = BN, CP = CN, DP = DQ. Сложив почленно эти равенства получим
АМ + ВМ + СР + DР = АQ + ВN + СN + DQ, или
Теорема 8. Если суммы противоположных сторон четырёхугольника равны, то в него можно вписать круг.
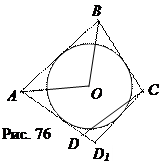
АВ + СD = АD + ВС. (1)
Проведём биссектрисы углов А и В. Тогда точка их пересечения находится на одинаковом расстоянии от сторон АD, АВ и ВС этого четырёхугольника. Проведём окружность с центром О и радиусом, равным расстоянию от точки О до прямой АВ. Этот круг касается сторон АD, АВ и ВС данного четырёхугольника. Докажем, что круг касается и стороны СD. Пусть СD1 – вторая касательная, проведённая из точки С (рис. 76). Тогда по теореме 7
Если точка D принадлежит отрезку АD1, то
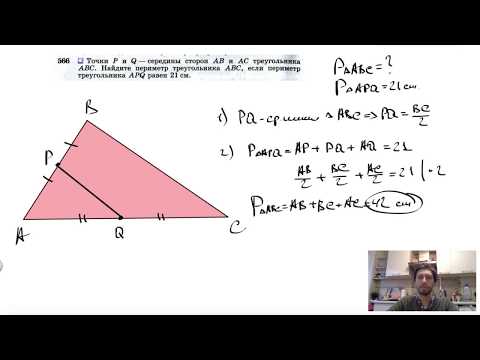
Видео:№566. Точки Р и Q — середины сторон АВ и АС треугольника ABC. Найдите периметр треугольникаСкачать
Точки P, Q, R и T на рисунке 86 — середины сторон четырехугольника ABCD. Докажите, что четырехугольник PQRT — параллелограмм.
Видео:ЕГЭ 2017 | Задание 3 | Диагонали четырехугольника равны ... ✘ Школа ПифагораСкачать

Ваш ответ
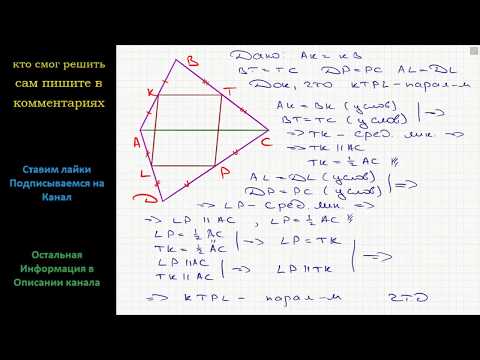
Видео:Геометрия Докажите, что середины сторон четырехугольника являются вершинами параллелограммаСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,680
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🎦 Видео
№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
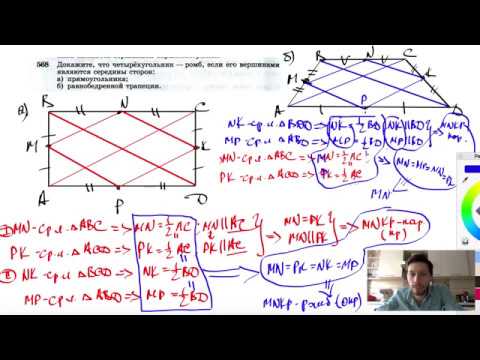
Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

38. Геометрия на ЕГЭ по математике. Задача на тему "Средняя линия треугольника"Скачать

№564. Дан треугольник, стороны которого равны 8 см, 5 см и 7 см. Найдите периметр треугольника,Скачать

Диагонали четырехугольника равны 4 и 5.Скачать

Решение задач пространственный четырехугольникСкачать

✓ Учимся не бояться задания 18 | ЕГЭ. Математика. Профиль | #ТрушинLive #019 | Борис Трушин |Скачать

№346. Точки М и N — середины оснований АВ и CD трапеции ABCD, а О — произвольнаяСкачать

Планиметрия_03_01Скачать

8 класс, 25 урок, Средняя линия треугольникаСкачать

Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

39. Геометрия на ЕГЭ по математике. Свойства трапеции.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ОГЭ по математике 2022. Геометрия. Решение задач 23-25Скачать

