Геометрия | 5 — 9 классы
Найти площадь четырехугольника если его диагонали взаимно перпендикулярны, а их длины равны 7 и 13.
S = 1 / 2d1xd2 = 1 / 2x7x13 = 45, 5.
- Докажите, что площадь выпуклого четырехугольника, диагонали которго взаимно перпендикулярны, равна половине произведения его диагоналей?
- Диагонали выпуклого четырехугольника ABCD взаимно перпендикулярны и длины их равны 12, 4см и 15см?
- Диагонали равнобедренной трапеции взаимно перпендикулярны?
- Диагонали четырехугольника взаимно перпендикулярны и точкой пересечения делятся пополам?
- Докажите, что площадь выпуклого четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей?
- Основание равнобочной трапеции равно 13, 7?
- Помогите, пожалуйста?
- В выпуклом четырехугольнике диагонали взаимно перпендикулярны?
- В четырехугольнике АВСD диагонали перпендикулярны и равны 4 и 11?
- Диагонали четырехугольника взаимно перпендикулярны?
- Нахождение площади выпуклого четырехугольника: формула и пример
- Формула вычисления площади
- По диагоналям и углу между ними
- По четырем сторонам (формула Брахмагупты)
- По радиусу вписанной окружности и сторонам
- Пример задачи
- Учебное пособие. Пенза-2012 удк 514
- Главная > Документ
- 🎥 Видео
Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольникаСкачать

Докажите, что площадь выпуклого четырехугольника, диагонали которго взаимно перпендикулярны, равна половине произведения его диагоналей?
Докажите, что площадь выпуклого четырехугольника, диагонали которго взаимно перпендикулярны, равна половине произведения его диагоналей.
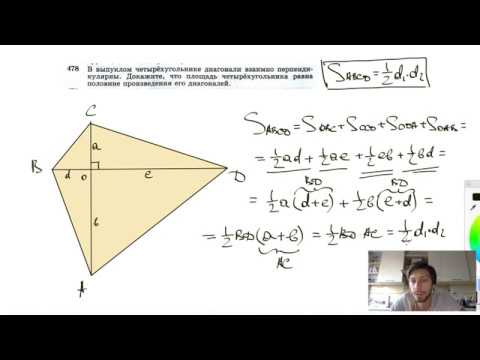
Видео:№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать
Диагонали выпуклого четырехугольника ABCD взаимно перпендикулярны и длины их равны 12, 4см и 15см?
Диагонали выпуклого четырехугольника ABCD взаимно перпендикулярны и длины их равны 12, 4см и 15см.
Найдите его площадь.
Видео:Геометрия Найдите площадь выпуклого четырехугольника диагонали которого равны 3√3 см и 4 см а уголСкачать

Диагонали равнобедренной трапеции взаимно перпендикулярны?
Диагонали равнобедренной трапеции взаимно перпендикулярны.
Найти площадь, если основания равны 12 и 16 см.
Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

Диагонали четырехугольника взаимно перпендикулярны и точкой пересечения делятся пополам?
Диагонали четырехугольника взаимно перпендикулярны и точкой пересечения делятся пополам.
Найдите периметр (в см) четырехугольника, если его диагонали равны 6см и 8см.
Видео:ОГЭ по математике. Площадь четырехугольника можно вычислить (вар. 4)Скачать

Докажите, что площадь выпуклого четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей?
Докажите, что площадь выпуклого четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Основание равнобочной трапеции равно 13, 7?
Основание равнобочной трапеции равно 13, 7.
Найти площадь трапеции, если ее диагонали взаимно перпендикулярны.
Видео:Задача 7Скачать

Помогите, пожалуйста?
Я геометрию хорошо понимаю (отличница), но именно этот пример не поняла))) Приведите примеры, опровергающие высказывания : а) если диагонали четырехугольника взаимно перпендикулярны, то этот четырехугольник является ромбом.
Б) если диагонали четырехугольника взаимно перпендикулярны и равны, то этот четырехугольник является ромбом.
Видео:Геометрия Диагонали выпуклого четырехугольника равны 8 см и 12 см а угол между ними 30 НайдитеСкачать

В выпуклом четырехугольнике диагонали взаимно перпендикулярны?
В выпуклом четырехугольнике диагонали взаимно перпендикулярны.
Докажите, что S четырехугольника равна половине произведения его диагоналей.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

В четырехугольнике АВСD диагонали перпендикулярны и равны 4 и 11?
В четырехугольнике АВСD диагонали перпендикулярны и равны 4 и 11.
Найти его площадь.
* * * * * Желательно с подробным решением)).
Видео:8 класс, 4 урок, ПараллелограммСкачать

Диагонали четырехугольника взаимно перпендикулярны?
Диагонали четырехугольника взаимно перпендикулярны.
Как называется этот четырехугольник ?
А) параллелограм б) прямоугольник в) ромб.
Перед вами страница с вопросом Найти площадь четырехугольника если его диагонали взаимно перпендикулярны, а их длины равны 7 и 13?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
Можно построить контр пример , так как этот угол из условия однозначный. Зададим сразу расстояние одной из прямых , пусть A1D1 , чтобы не вписывать множество переменных для произвольного шестиугольника , определим координаты 5 вершин произвольным об..
Вот я прикрепил файл. Там все доказано.
Представим треугольник ДВС, тогда один из этих углов будет 60 градусов добавим к этому треугольнику точно такой — же треугольник, то получится, что все углы будут равны, а значит и стороны будут равны. Разделим сторону ДС на пополам, а когда все сто..
Угол 1 = углу 2, угол 6 = углу 3, угол 5 = углу 2 = 112 градусов. Допустим угол6 это Х, тогда угол1 это Х + 10 Тогда угол1 + угол6 + угол5 = 180 градусов. Х + 10 + х + 112 = 180 2х + 122 = 180 2х = 180 — 122 = 58 х = 58 : 2 = 29 — угол 6 и угол 3 т..
Характеристика равнин Равнина — это участок суши или дна моря, имеющий небольшое колебание высот (до 200 м) и незначительный уклон (до 5º). Они встречаются на разных высотах, в том числе и на дне океанов. Отличительная черта равнин — четкая, открыт..
Пусть большая сторона равна Х, тогда вторая сторона (Х — 10). Cos60° = 1 / 2. Сторона против угла 60° равна 14 (дано). По теореме косинусов : 14² = Х² + (Х — 10)² — 2 * Х * (Х — 10) * (1 / 2). Или 196 = Х² + (Х² — 20Х + 100) — Х² + 10Х. Х² — 10Х..
AC — 12 CB — 11 Это очень легко я давно проходила.
У равн. Треугольника боковые стороны равны значиь вторая сторона = 26см что бы найти площадь , нужно узнать высоту, для этого мы чертим высоту, она разделяет равнобедренный треуг. На два прямоугольных, сторона основания прям треуг = 20÷2 = 10см, Вы..
Видео:Задача 8 ЕГЭ по математике #2Скачать

Нахождение площади выпуклого четырехугольника: формула и пример
Выпуклый четырехугольник – это геометрическая фигура, полученная путем соединения на плоскости четырех точек, которые не должны лежать на одной прямой. При этом образованные таким образом стороны не должны пересекаться.
Видео:ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Формула вычисления площади
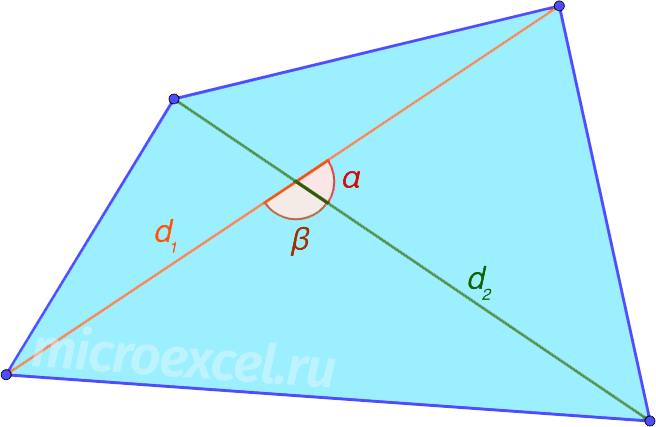
По диагоналям и углу между ними
Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.
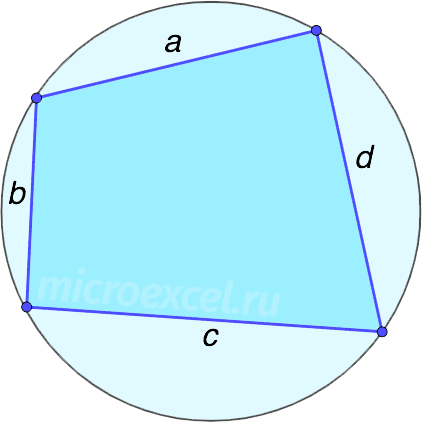
По четырем сторонам (формула Брахмагупты)
Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.
p – полупериметр, вычисляется следующим образом:
По радиусу вписанной окружности и сторонам
Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:
S = p ⋅ r
r – радиус окружности.
Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Пример задачи
Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.
Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см 2 .
Видео:Задача 8 ЕГЭ по математике #1Скачать

Учебное пособие. Пенза-2012 удк 514
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
§ 12. Площадь четырехугольника.
Площадь параллелограмма вычисляется по формулам:


где a и b – стороны параллелограмма, h a и h b – высоты к ним, – угол между сторонами параллелограмма.
Т
Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними.

Диагонали ромба перпендикулярны, следовательно, площадь ромба равна половине произведения его диагоналей.
Площадь прямоугольника вычисляется по формуле

где a и b – смежные стороны прямоугольника.
Площадь квадрата со стороной а вычисляется по формуле

Площадь трапеции с основаниями a и b и высотой h вычисляется по формуле

Задача 1. В окружности радиуса 13 через точку А, лежащую на диаметре МР, под углом 30 проведена хорда QN. Найти площадь четырехугольника MNPQ, если МА = 3.
Д
Найти: 
По теореме площадь четырехугольника MNPQ равна 
Чтобы определить ее, надо найти хорду QN.
Так как МА = 3, то АО = МО – МА = 10.
Проведем ОD QN. QD = DN (так как QON – равнобедренный, высота ОD, опущенная на основание треугольника, является медианой).


Из прямоугольного треугольника DОN находим DN:


Рассмотрим несколько задач, где определяется или используется площадь трапеции.
З
Дано: АВСD – трапеция,
Найти: 
Проведем СЕ || ВА и NF || ВА, а также СК MN и NР АD.
Пусть СК = h 1 , NP = h 2 .
Так как СЕ || NF, то ЕСN = FND, а из того, что MN || AD следует ENC = FDN. Следовательно, ECN FND (по двум углам).
Из подобия треугольников имеем 


Из подобия 


Если площадь трапеции MBCN – S 1 , а площадь трапеции АМND – S 2 , то 


Ответ: 
З
Дано: АВСD – трапеция,
S AOD = S 1 , S AOD = S 2 .
Пусть ВС = а , АD = b , и пусть h – высота трапеции.
Известно, что диагонали трапеции разбивают ее на четыре треугольника с общей вершиной. Площади треугольников, прилежащих к боковым сторонам равны. Следовательно, 



Так как 






Отсюда находим 
Ответ: 
Задача 4. В треугольнике АВС биссектрисы АD и BF пересекаются в точке О. Известно, что точки F, О, D и С лежат на одной окружности и что DF = 
Д
АD, BF – биссектрисы,
F, O, D, C , DF = 
Так как 

Четырехугольник ODCF вписан в окружность, следовательно, 

учитывая, что 
Заметим, что СО – биссектриса С, следовательно, вписанные углы ОСD и OCF – равны.
ODF = OFD = FСО = OСD (как вписанные углы, опирающиеся на равные дуги).
Таким образом, ODF = OFD = 

Найдем его высоту, опущенную из вершины С: 

Ответ: 
Задача 5. Около окружности радиуса 5 см описана равнобедренная трапеция. Расстояние между точками касания ее боковых сторон равно 8 см. Найти площадь трапеции.
Д
N, K, L, M – точки касания,



Рассмотрим 

Кроме того, NMK = 90, так как он опирается на диаметр NK, АОВ = 90 (биссектрисы двух односторонних углов, образованных двумя параллельными прямыми при пересечении их третьей, пересекаются под прямым углом).
Отсюда, 


где k – коэффициент подобия треугольников,



В трапецию АВСD вписана окружность суммы противолежащих сторон трапеции равны, то есть 2АВ = ВС + АD 

Задача 6. Дан квадрат со стороной равной а . Если на двух противоположных сторонах этого квадрата построить внутри его два правильных треугольника, то боковые стороны треугольников пересекутся и образуют четырехугольник. Определить вид полученного четырехугольника и вычислить его углы, стороны и площадь.

Из построения очевидно, что искомый четырехугольник EMFN – ромб с углами, равными 60 и 120.



Тогда большая диагональ ромба

Из прямоугольного треугольника ЕОМ имеем: 




Но сторона ромба равна его меньшей диагонали, следовательно, искомая площадь ромба

Ответ: 
Задачи для самостоятельного решения.
Точка D лежит на стороне АВ треугольника АВС, точка F – на стороне АС. Отрезки СD и BF пересекаются в точке О. Известно, что AF:FC = 3:1 и АD:DВ = 7:2. Какую часть площади треугольника АВС составляет площадь четырехугольника АDОF?
Углы при большем основании трапеции равны 30 и 60. Средняя линия трапеции равна 6, а отрезок, соединяющий середины оснований, равен 4. Найти площадь трапеции.
Окружность, вписанная в равнобокую трапецию АВСD, касается большего основания АD в точке К и боковой стороны АВ в точке Р. Отрезок РК пересекает диагональ АС в точке М, так что АМ:МС = 4:3. Периметр трапеции равен 20. Найти ее площадь.
В ромбе АВСD, диагонали которого равны 15 м и 20 м, из вершины С тупого угла проведены две высоты: СЕ и CF. Вычислить площадь четырехугольника АЕСF.
Диагонали ромба относятся как 3:4. Определить отношение площади ромба к площади круга, вписанного в ромб.
Точка М внутри круга радиуса R удалена от центра на расстояние, равное а . Через точку М проведены диаметр и две взаимно перпендикулярные хорды, одна из которых образует с диаметром угол = 45. Вычислить площадь вписанного в круг четырехугольника, имеющего эти хорды диагоналями.
Около окружности радиуса R описан параллелограмм. Площадь четырехугольника с вершинами в точках касания окружности и параллелограмма равна S . Найти длина сторон параллелограмма.
В полукруге расположен прямоугольник АВСD так, что его сторона АВ лежит на диаметре, ограничивающем полукруг, а вершины С и D – на ограничивающей полукруг дуге. Длина радиуса полукруга равна 5 см. Найти длины сторон прямоугольника АВСD, если его площадь равна 24 см 2 , а длина диагонали больше 8 см.
Длина средней линии равнобочной трапеции равна 10. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно 7/13. Найти длину высоты трапеции.
В четырехугольнике АВСD сторона АВ равна стороне ВС, диагональ АС равна стороне СD, а угол АВС равен углу АСD. Радиусы окружностей, вписанных в треугольники АВС и АСD, относятся как 3:4. Найти отношение площадей этих треугольников.
В окружность радиуса R вписана трапеция, у которой боковая сторона равна меньшему основанию, а угловая мера дуги, стягиваемой этим основанием, равна . Найдите площадь трапеции.
Определите площадь равнобедренной трапеции, у которой длины оснований равны 10 см и 26 см, а диагонали перпендикулярны боковым сторонам.
Дана трапеция MNPQ с основаниями MQ и NP. Прямая, параллельная основаниям, пересекает боковую сторону MN в точке А, а сторону PQ – в точке В. S ANPQ :S MABQ = 2:7. Найдите АВ, если NP = 4, MQ = 6.
В полукруг единичного радиуса вписана трапеция так, что ее основание лежит на диаметре. Найти площадь трапеции, если ее периметр равен 5.
Стороны треугольника 20, 34 и 42 см. Найти площадь вписанного прямоугольника, если известно, что его периметр равен 45см.
Окружность касается сторон АВ и АD прямоугольника АВСD, проходит через вершину С и пересекает сторону DС в точке К. Найти площадь четырехугольника АВКD, если АВ = 9 см, АD = 8 см.
Внутри прямоугольника АВСD взята точка М так, что АМ = 
В круг радиуса R вписаны равносторонний треугольник и квадрат, имеющие общую вершину. Вычислить площадь общей части треугольника и квадрата.
Около окружности радиуса R = 1 см описана равнобедренная трапеция, площадь которой равна 5 см 2 . Найти площадь четырехугольника, вершинами которого служат точки касания окружности и трапеции.
Из каждой вершины основания равностороннего треугольника со стороной а проведены два луча, образующих с этим основанием углы 15 и 30. Найти площадь четырехугольника, вершинами которого являются точки пересечения построенных лучей.
В трапецию, у которой меньшее основание равно а , вписана окружность. Одна из боковых сторон трапеции делится точкой касания на отрезки длиной т и п , считая от большего основания. Определить площадь трапеции.
🎥 Видео
Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Миникурс по геометрии. ЧетырехугольникиСкачать

Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

Найдите площадь четырёхугольникаСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать