Пучок параллельных прямых на плоскости это (7 видео)

Пучок прямых. Уравнение пучка прямых

В данной статье мы рассмотрим понятие пучка прямых. Представим уравнение пучка прямых. Приведем примеры нахождения уравнения пучка прямых, проходящих через данную точку.

Пучком прямых называется множество прямых, проходящих через данную точку P. P называется центром пучка прямых . Две разные прямые в пучке прямых определяют центр пучка прямых.

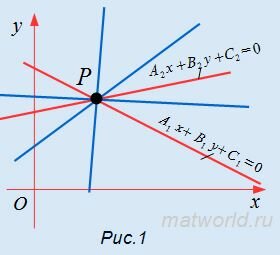Пучок параллельных прямых на плоскости это

Найдем уравнение пучка прямых, центром которого служит точка пересечения двух прямых (Рис.1):

A₁x+B₁y+C₁=0

(1)

A₂x+B₂y+C₂=0.

(2)

Докажем следующую теорему.

Теорема 1. Пусть (1) и (2) уравнения двух прямых, пересекающихся в точке P, а λ₁ и λ₂ некоторые числа, которые одновременно не равны нулю. Тогда

λ₁(A₁x+B₁y+C₁) +λ₂(A₂x+B₂y+C₂)=0.

(3)

является уравнением прямой, проходящей через точку P. Обратно, любая прямая, проходящая через точку P определяется уравнением (3), при некотороых числах λ₁ и λ₂.

Доказательство. Во первых покажем, что уравнение (3) является линейным уравнением (уравнением первого порядка), т.е. уравнением, при котором коэффициент при x или y не равен нулю.

Группируем коэффициенты при x и y:

(λ₁A₁+λ₂A₂)x+(λ₁B₁+λ₂B₂)y+(λ₁C₁+λ₂C₂)=0

(4)

λ₁A₁+λ₂A₂=0, λ₁B₁+λ₂B₂=0.

(5)

Тогда, например при λ₁≠0 (по условию теоремы хотя бы один из чисел λ₁ и λ₂ не равен нулю), получим:

(6)

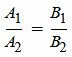(7)

Полученное равенство является условием параллельности прямых, определяемых уравнениями (1) и (2), что противоречит условию теоремы (эти прямые пересекаются и не совпадают). Таким образом хотя бы один из равенств (5) не выполняется, т.е. хотя бы один коэффициент при x и y в уравнении (4) не равен нулю. Отсюда следует, что уравнение (4) является линейным уравнением (уравнением первой степени) и является уравнением некоторой прямой. По условию теоремы, эта прямая проходит через точку P(x₀, y₀), которая является пересечением прямых (1) и (2), т.е. выполняются равенства:

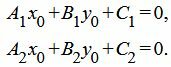(8)

Из уравнениий (8) следует, что при любых λ₁ и λ₂:

λ₁(A₁x₀+B₁y₀+C₁)+λ₂(A₂x₀+B₂y₀+C₂)=0,

т.е. уравнение (3) проходит через точку P.

Докажем вторую часть теоремы. Покажем, что любая прямая, проходящая через точку P определяется уравнением (3) при некоторых значениях λ₁ и λ₂.

Возьмем некоторую прямую проходящую через точки P и M’(x’, y’). Покажем, что данная прямая определяется уравнением (3) при некоторых значениях λ₁ и λ₂, не равных одновременно нулю.

В первой части доказательства теоремы мы показали, что прямая, проходящая через точку P определяется уравнением (3). Теперь, если эта прямая проходит через еще одну точку M’(x’, y’), то координаты этой точки должны удовлетворять уравнению (3):

λ₁(A₁x’₀+B₁y’₀+C₁)+λ₂(A₂x’₀+B₂y’₀+C₂)=0,

(9)

Заметим, что выражения в скобках не могут быть равным нулю одновременно, т.к. это означало бы, что оба уравнения проходят через точки P и M’(x’, y’) и, следовательно, совпадают. Пусть, например, λ₁(A₁x’₀+B₁y’₀+C₁)≠0. Тогда задав λ₂ произвольное число, отличное от нуля, решим (9) относительно λ₁:

Пример 1. Пучок прямых задан уравнениями:

Найти уравнение прямой из пучка прямых, проходящий через точку M(−3, 1).

Решение. Уравнение пучка прямых, заданных прямыми (10) и (11) имеет следующий вид:

λ₁(2x+3y−1)+λ₂(x−4y+2)=0.

(12)

Подставим координаты точки M в уравннение (12):

λ₁(2·(−3)+3·1−1)+λ₂(−3−4·1+2)=0.

(13)

−5(2x+3y−1)+4(x−4y+2)=0.

(14)

Упростив уравнение (14), получим уравнение из пучка прямых проходящих через точку M(−3, 1):

Пример 2. Построить уравнение пучка прямых с центром M(4,1):

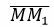
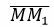
Решение. Возьмем две различные точки, не совпадающие с точкой M: M₁(2,1), M₂(−1,3). Построим уравнение, проходящие через точки M и M₁. Нормальный вектор n₁ этой прямой должен быть ортогональным вектору , равному разностьям координат точек M и M₁: ==. Т.е. можно взять n₁=. Тогда уравнение прямой с нормальным вектором n₁, проходяще через точку M имеет следующий вид:

Построим уравнение проходящее через точки M и M₂. 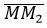==. Возмем в качестве нормального вектора второго уравнения n₂=. Тогда второе уравнение имеет слеждующий вид:

2x+5y−13=0.

(16)

Из уравнений (15) и (16) можно записать уравнение пучка прямых с центром M(4,1):

λ₁(y−1)+λ₂(2x+5y−13)=0.

Заметим, что взяв другие точки M₁ и M₂, мы получим уравнение того же пучка прямых, но с другими двумя прямыми.

Содержание

Пучок прямых, уравнение пучка прямых
Пучок прямых – это определение
Уравнение пучка прямых – решение задач
Окружность, эквидистанта и орицикл
📹 Видео

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Пучок прямых, уравнение пучка прямых

В статье рассматриваются определения пучка прямых с центром в заданной точке плоскости. Разбирается подробное решение с применением определения, рассматриваются задачи на составление уравнения пучка прямых, нахождение координат.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Пучок прямых – это определение

Пучок прямых определяется на плоскости, но не в трехмерном пространстве. Аксиома геометрии говорит о том, что если имеются две несовпадающие точки, расположенные на плоскости, то через них можно провести только одну прямую. Если на плоскости γ задается точка М 0 и M 1 , то через них можем провести прямую. Когда имеется еще одна точка М 2 , которая не лежит на прямой М 0 М 1 , тогда можно провести прямую М 0 М 2 . Если отметим точку М 3 , не принадлежащую ни одной из проведенных прямых, через нее также може провести прямую, проходящую через М 0 .

Отсюда следует, что в плоскости γ можно провести множество прямых через заданную точку. Это и привело к определению пучка прямых.

Заданная плоскость γ с множеством всех прямых, которые лежат в плоскости γ и проходящие через точку М 0 называют пучком прямых с центром в точке М 0 .

Исходя из определения, имеем, что любые две прямые из этого пучка пересекутся в центре данного пучка прямых. Пучок определяется при условии, если указан центр данного пучка.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Уравнение пучка прямых – решение задач

Для решения задач применяется уравнение пучка прямых, то есть сам пучок рассматривается относительно систему координат О х у на плоскости.

Когда имеем на плоскости прямоугольную систему координат О х у с указанными пересекающимися прямыми а 1 и а 2 _, пучок задает эти прямые. За систему координат О х у отвечает общее уравнение прямой, которое имеет вид A 1 x + B 1 y + C 1 = 0 или A 2 x + B 2 y + C 2 = 0 .

Введем обозначение пересечения прямых как точка М 0 с координатами х 0 и y 0 . Отсюда следует, что точка М имеет координаты M 0 ( x 0 , y 0 ) .

Чтобы определить вид используемого уравнения в пучках, рассмотрим на теореме.

При заданных двух пересекающихся прямых а 1 и а 2 имеются прямые, которые входят в пучок прямых, образованных в системе координат О х у . Их уравнения имеют вид A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 тогда и только тогда, когда уравнение прямой α · ( A 1 x + B 1 y + C 1 = 0 ) + β · ( A 2 x + B 2 y + C 2 ) = 0 соответствует ей,a α и β являются действительными числами, неравными нулю. Данное условие записывается так: α 2 + β 2 ≠ 0 .

Начнем рассмотрение доказательства с рассмотрения прямой a с указанного пучка, после чего докажем, что ее можно задавать при помощи уравнения α · ( A 1 x + B 1 y + C 1 ) + β · ( A 2 x + B 2 y + C 2 ) = 0 .

Центр пучка возьмем за точку с координатами M 0 = ( x 0 , y 0 ) .

Отсюда получаем, что n → = ( A 1 , B 1 ) является нормальным вектором прямой A 1 x + B 1 y + C 1 = 0 , тогда n 2 → = ( A 2 , B 2 ) — нормальный вектор для прямой A 2 x + B 2 y + C 2 = 0 . Получаем, что n → 1 и n 2 → — это неколлинеарные векторы, потому что у прямой а 1 и а 2 нет общих точек пересечения. Значит, необходимо разложить нормальный вектор n → по двум неколлинеарным n 1 → и n 2 → . Разложение необходимо выполнять по формуле n → = α · n 1 → + β · n 2 → . В итоге получаем, что n → = ( α · A 1 + β · A 2 , α · B 1 + β · B 2 ) .

После вычислений получаем координаты нормального вектора прямой a , равные n → = α · A 1 + β · A 2 , α · B 1 + β · B 2 . Координаты точки, пересекающиеся с прямой a в точке M 0 ( x 0 , y 0 ) , записываются при помощи общего уравнения прямой a . Тогда получаем выражение вида:

α · A 1 + β · A 2 · x — x 0 + α · B 1 + β · B 2 · y — y 0 = 0 ⇔ ⇔ α · ( A 1 x + B 1 y — A 1 x 0 + B 1 y 0 ) + β · A 2 x + B 2 y — A 2 x 0 — B 2 y 0 = 0

По — A 1 x 0 — B 1 y 0 = C 1 и — A 2 x 0 — B 2 y 0 = C 2 получим общее уравнение прямой a , имеющее вид α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 . Вышесказанная необходимость доказана.

Осталось найти доказательства достаточности.

Значит, нужно произвести доказательство выражения α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 , где имеем α и β некоторыми действительными числами неравными нулю, существует уравнение из пучка прямых с точкой пересечения M 0 ( x 0 , y 0 ) . Такое уравнение определено при помощи двух пересекающихся прямых A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Запишем уравнение α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 в виде α · A 1 + β · A 2 · x + α · B 1 + β · B 2 · y + α · C 1 + β · C 2 = 0 .

Уравнение будет считаться общим, если выполняется условие, когда α · A 1 + β · A 2 и α · B 1 + β · B 2 отличны от нуля. Иначе мы получили выражение вида α · A 1 + β · A 2 = 0 ⇔ A 1 = — β α · A 2 и α · B 1 + β · B 2 = 0 ⇔ B 1 = — β α · B 2 или α · A 1 + β · A 2 = 0 ⇔ A 2 = — α β · A 1 и α · B 1 + β · B 2 = 0 ⇔ B 2 = — α β · B 1 . Это значило бы, что векторы не коллинеарны.

Это невозможно в данном случае, так как n 1 → и n 2 → — это нормальные векторы прямых а 1 и а 2 , которые пересекаются.

Имеем, что уравнение α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 является общим уравнением прямой. Далее необходимо произвести доказательство удовлетворения координат точки при их пересечении, то есть координаты точки M 0 ( x 0 , y 0 ) . Докажем, справедливо ли равенство α · ( A 1 x + B 1 y + C 1 ) + β · A 2 x + B 2 y + C 2 = 0 .

M 0 ( x 0 , y 0 ) является точкой пересечения прямых, значит, ее координаты должны удовлетворять уравнениям обеих пересекающихся прямых.

Когда A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 справедливы, отсюда следует, что α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = α · 0 + β · 0 = 0 .

Что и требовалось доказать.

Можем сделать вывод, что уравнение, которое имеет вид α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = 0 и есть уравнение пучка.

Значения α и β необходимы для того, чтобы определять прямые, находящиеся в данном пучке, с уравнениями A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Необходимо, чтобы как минимум один из параметров был не равен нулю, тогда можно упростить выражение. При условии, что α ≠ 0 получаем выражение вида A 1 x + B 1 y + C 1 + λ · A 2 x + B 2 y + C 2 = 0 с λ = α β .

При β ≠ 0 выражение принимает вид μ · A 1 x + B 1 y + C 1 + A 2 x + B 2 y + C 2 = 0 с μ = α β .

Они не являются эквивалентными уравнению пучка прямых, относящихся к виду α · A 1 x + B 1 y + C 1 + β · A 2 x + B 2 y + C 2 = 0 . Уравнение A 1 x + B 1 y + C 1 + λ · A 2 x + B 2 y + C 2 = 0 при любых значениях λ не даст возможности получить уравнение вида A 2 x + B 2 y + C 2 = 0 .

Уравнение μ · A 1 x + B 1 y + C 1 + A 2 x + B 2 y + C 2 = 0 при любых значениях μ не даст в результате A 1 x + B 1 y + C 1 = 0 .

Подробно рассмотрим на решении примеров.

Написать уравнение прямой пучка с заданным центром в точке M 0 ( — 1 , 4 ) , k = 3 .

Необходимо составить уравнение прямой, которая будет проходить через заданную точку с координатами M 0 ( — 1 , 4 ) с угловым коэффициентом равным 3 . Тогда запишем уравнение прямой с угловым коэффициентом и получим y — 4 = 3 · ( x — ( — 1 ) ) ⇔ y = 3 x + 7 .

Ответ: y = 3 x + 7 .

Найти координаты центра пучка прямых в О х у , если известны два уравнения пересекающихся прямых x — 4 2 = y + 3 0 и x 2 3 + y — 1 = 1 .

Чтобы найти координаты центра пучка, необходимо найти точки пересечения x — 4 2 = y + 3 0 и x 2 3 + y — 1 = 1 .

Получим, что каноническое уравнение прямой на плоскости x — 4 2 = y + 3 0 эквивалентно x 2 3 + y — 1 = 1 , а уравнение в отрезках x 2 3 + y — 1 = 1 общему уравнению прямой 3 2 x — y — 1 = 0 .

Теперь составляем систему уравнений, включающую в себя уравнения прямых.

y + 3 = 0 3 2 x — y — 1 = 0 ⇔ y = — 3 3 2 x — ( — 3 ) — 1 = 0 ⇔ y = — 3 x = — 4 3

Получим, что — 4 3 , — 3 — это координаты центральной точки, где пересекаются все прямые.

Произвести составление уравнения пучка прямых в О х у , которое задано при помощи прямых 3 x — 2 y + 1 = 0 и x = — 2 + 2 · λ y = 5 · λ , имеющих общую точку пересечения.

Для начала необходимо получить общее уравнение прямой. Оно определено параметрическим уравнением x = — 2 + 2 · λ y = 5 · λ .

Отсюда следует, что

x = — 2 + 2 · λ y = 5 · λ ⇔ λ = x + 2 2 λ = y 5 ⇔ x + 2 2 = y 5 ⇔ ⇔ 5 · ( x + 2 ) = 2 · y ⇔ 5 x — 2 y + 10 = 0

Произведем запись уравнения пучка прямых и получим α · ( 3 x — 2 y + 1 ) + β · ( 5 x — 2 y + 10 ) = 0 , а α и β являются действительными числами, где обязательным условием считается α 2 + β 2 ≠ 0 .

Ответ: α · ( 3 x — 2 y + 1 ) + β · ( 5 x — 2 y + 10 ) = 0 .

Написать уравнение прямой, проходящей через точку M 1 ( 2 , — 1 ) и принадлежащей пучку прямых с уравнением α · ( 5 x + y — 19 ) + β · ( 2 x — 3 y + 6 ) = 0 .

Задача решается двумя способами.

Первый способ начинается с определения М 0 , являющейся центром пересечения. Тогда нужно найти точки пересечения уравнений 5 x + y — 19 = 0 и 2 x — 3 y + 6 = 0 , а их результат и будет являться координатами для M 0 .

Определяем координаты, решив получившуюся систему:

5 x + y — 19 = 0 2 x — 3 y + 6 = 0 ⇔ y = 19 — 5 x 2 x — 3 · ( 19 — 5 x ) + 6 = 0 ⇔ y = 19 — 5 x x = 3 ⇔ ⇔ y = 19 — 5 · 3 x = 3 ⇔ y = 4 x = 3

Значит точка М 0 имеет координаты ( 3 , 4 ) . Это записывается как M 0 ( 3 , 4 ) . Чтобы получить искомое уравнение , которое проходит через точки с координатами M 0 ( 3 , 4 ) и M 1 ( 2 , — 1 ) . В итоге получаем:

x — 3 2 — 3 = y — 4 — 1 — 4 ⇔ x — 3 — 1 = y — 4 — 5 ⇔ x — 3 1 = y — 4 5

Второй способ начинается с того, что необходимо определить параметры α и β , чтобы уравнение α · ( 5 x + y — 19 ) + β · 2 x — 3 y + 6 = 0 было уравнением прямой, которая проходит через M 1 ( 2 , — 1 ) . Для этого найдем координаты М 1 и получим, что

α · 5 · 2 + ( — 1 ) — 19 + β · 2 · 2 — 3 · ( — 1 ) + 6 = 0 ⇔ ⇔ — 10 · α + 13 · β = 0 ⇔ α = 13 · β 10

Принимаем значение β = 10 , при желании можно выбирать любое другое такое значение β , которое дает несложное вычисление α . Получаем α = 13 · β 10 = 13 · 10 10 = 13 .

При подстановке значений α = 13 и β = 10 в заданное уравнение пучка, преобразуем:

13 · ( 5 x + y — 19 ) + 10 · ( 2 x — 3 y + 6 ) = 0 ⇔ 85 x — 17 y — 187 = 0 ⇔ 5 x — y — 11 = 0

Необходимо проверить эквивалентность получившихся уравнений.

x — 3 1 = y — 4 5 ⇔ 5 · x — 3 = 1 · y — 4 ⇔ 5 x — y — 11 = 0

Отсюда следует, что все решено верно.

Ответ: 5 x — y — 11 = 0 .

Определить принадлежность прямой 3 x — y + 5 = 0 пучку прямых α · ( x — 2 y + 4 ) + β · ( x — y + 4 ) = 0 .

Решение производится двумя способами.

Первый способ решения начинается с нахождения центров координаты заданного уравнения пучка и их проверки:

x — 2 y + 4 = 0 x — y + 4 = 0 ⇔ x = 2 y — 4 x — y + 4 = 0 ⇔ x = 2 y — 4 2 y — 4 — y + 4 = 0 ⇔ ⇔ x = 2 y — 4 y = 0 ⇔ x = 2 · 0 — 4 y = 0 ⇔ x = — 4 y = 0 3 · ( — 4 ) — 0 + 5 = 0 ⇔ — 7 = 0

Получим, что подстановка координат центра в уравнение прямой 3 x — y + 5 = 0 дает неверное равенство. Делаем вывод, что прямая не пересекает центр пучков, значит, и не принадлежит ему.

Второй способ начинается с раскрытия скобок и приведения подобных слагаемых α · ( x — 2 y + 4 ) + β · x — y + 4 = 0 ⇔ 2 α + β · y + 4 α + 4 β = 0 .

Когда прямая 3 x — y + 5 = 0 принадлежит пучку прямых, тогда имеются такие значения α и β , что два уравнения α + β · x — 2 α + β · y + 4 α + 4 β = 0 и 3 x — y + 5 = 0 являются эквивалентными.

Тогда получаем систему, состоящую из трех равнений α + β = 3 2 α + β = 1 4 α + 4 β = 5 .

Для ее преобразования необходимо приравнять коэффициенты перед переменными x и y и свободные членов имеющихся уравнений α + β · x — 2 α + β · y + 4 α + 4 β = 0 и 3 x — y + 5 = 0 , чтобы получать результат решения.

Для проверки необходимо применить теорему Кронекера-Капелли.

Для этого необходимо записать основную и расширенную матрицы для составленной системы уравнений. Получим, что A = 1 1 2 1 4 4 и T = 1 1 3 2 1 1 4 4 5 .

Требуется посчитать ранг матрицы A . Он равен 2 , потому что 1 1 2 1 = — 1 ≠ 0 .

Результат нахождения ранга расширенной матрицы равняется 3 , потому как 1 1 3 2 1 1 4 4 5 = 7 ≠ 0 .

Отсюда имеем, что система уравнений α + β = 3 2 α + β = 1 4 α + 4 β = 5 не определена, то есть имеет решений. Так как решения отсутствуют, прямая не проходит через центр прямой имеющихся пучков прямых.

Ответ: нет, прямая 3 x — y + 5 = 0 не принадлежит заданному пучку прямых, записанных уравнением вида α · ( x — 2 y + 4 ) + β · ( x — y + 4 ) = 0 .

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Окружность, эквидистанта и орицикл

1. На плоскости Лобачевского существуют три различных типа пучков, а именно: а) пучок пересекающихся прямых, т.е. множество всех прямых плоскости, проходящих через одну точку — центр пучка (рис. 231 ,а);

б) пучок расходящихся прямых, т.е. множество всех прямых плоскости, перпендикулярных к данной прямой (рис. 231, б); в) пучок параллельных прямых — множество прямых, состоящее из некоторой направленной прямой и всех направленных прямых, параллельных ей (рис. 231, в).

Ясно, что если задан пучок, то через любую точку плоскости (отличную от центра пучка пересекающихся прямых) проходит одна и только одна прямая пучка.

С каждым пучком прямых связаны определенные линии, которые мы рассмотрим в следующих пунктах этого параграфа.

2. Окружность. Как известно из школьного курса геометрии, окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки (центра окружности). Это определение относится к абсолютной геометрии, поэтому окружность — линия как евклидовой плоскости, так и плоскости Лобачевского. Многие теоремы об окружности, известные учащемуся из курса геометрии средней школы, доказываются без помощи аксиомы параллельных, поэтому они справедливы и на плоскости Лобачевского. Прежде всего отметим теорему о том, что любая прямая, лежащая в плоскости окружности, пересекается с ней не более чем в двух точках. Перечислим другие свойства окружности, которые относятся к абсолютной геометрии. При этом рассмотрим только те свойства, которые относятся к расположению точек окружности по отношению к пучку пересекающихся прямых с центром в центре окружности. Прямые этого пучка называются осями окружности.
1°. Окружность симметрична относительно любой своей оси.
2°. В каждой точке окружности существует касательная, которая перпендикулярна к оси, проходящей через точку касания.

Учитывая это свойство, мы можем говорить, что окружность пересекает свои оси под прямым углом или что окружность есть ортогональная траектория пучка прямых с центром в центре окружности (рис. 232, а).

Прямая АВ, где А е а н В А’ММ₂ ф Z В’М₂М (см. рис. 237, на этом рисунке Z А’ММ₂ Z В’М_ХМ, так как Z В’М₂М — внешний угол треугольника М_ХММ₂). Поэтому ММ_Х — единственная секущая равного наклона к прямым АА ‘и В В’, я

Пусть на плоскости задан пучок параллельных прямых. На множестве Q всех точек плоскости введем бинарное отношение Д следующим образом. Будем говорить, что точки А и В находятся в отношении Д, если они совпадают или прямая АВ является секущей равного наклона к прямым данного пучка, проходящим соответственно через точки А и В. Из этого определения непосредственно следует, что отношение Д удовлетворяет условиям рефлексивности и симметричности. Можно также доказать, что оно удовлетворяет условию транзитивности. Каждый элемент фактор-множества Г2/Д называется орициклом (или предельной линией). Прямые данного пучка называются осями орицикла. Если задан пучок параллельных прямых, то через каждую точку И плоскости проходит один и только один орицикл, который представляет собой класс эквивалентности К_А по отношению Д. Это множество состоит из точки А и всех таких точек X плоскости, что АХ — секущая равного наклона к прямым данного пучка, проходящим через точки А иХ.

Из предыдущего изложения ясно, что если даны направленная прямая UVи на ней некоторая точка А, то тем самым однозначно определяется орицикл, проходящий через точку И с осью UV.

Свойства орицикла аналогичны свойствам окружности и эквиди- станты.

Теорема 2. Любая прямая, лежащая в плоскости орицикла, пересекается с орициклом не более чем в двух точках.

и Допустим, что некоторая прямая имеет с орициклом три общие точки А, В и С, которые обозначены так, что А — В —С. Обозначим через АА’, ВВ’и ССоси орицикла, проходящие через эти точки. По определению АА‘|| ВВ’и ВВ’I СС. Отсюда следует, что точки И’, В’и С’лежат в одной полуплоскости с границей АВ (рис. 238).

По определению орицикла Zl=Z2nZ3=Z4 (см. рис. 238). Так как параллельные прямые не имеют общего перпендикуляра, то углы

1, 2, 3 и 4 не являются прямыми углами. Ни один из этих углов не может быть также и тупым углом. В самом деле, если, например, Z 1 и Z 2 тупые, то Z 3, смежный с Z 2, острый (см. рис. 238). Отложив от луча АВ угол МАВ, равный Z 3, как показано на рисунке 238, мы получаем луч AM, лежащий внутри угла А ‘АВ и не пересекающий луч В В’ (§ 69, лемма 1). Это противоречит определению параллельности прямых АА’ и В В’.

Таким образом, Z 2 и Z 3 — острые углы. Но эти углы смежные, поэтому мы пришли в противоречие с теоремой о смежных углах. ? Предлагаем учащемуся самостоятельно убедиться в том, что свойства 1°—4°, сформулированные для окружности и эквидистанты, имеют место и для орицикла. В частности, орицикл симметричен относительно любой своей оси и является ортогональной траекторией пучка его параллельных осей (см. рис. 232, в).

Можно доказать, что любые два орицикла на плоскости Лобачевского равны.