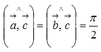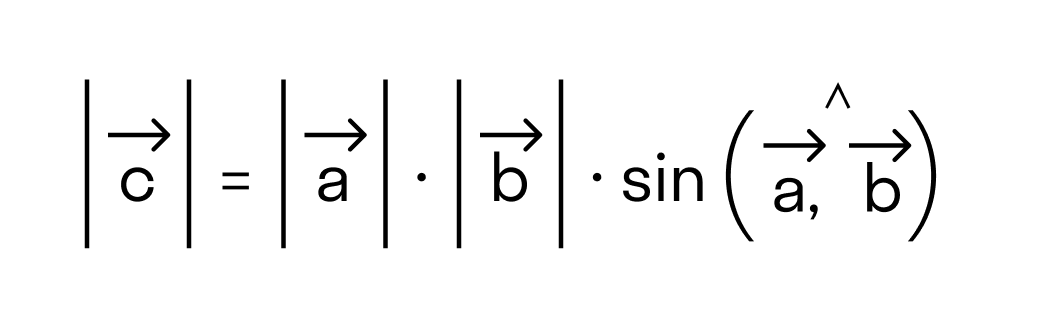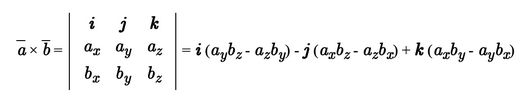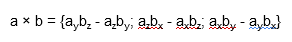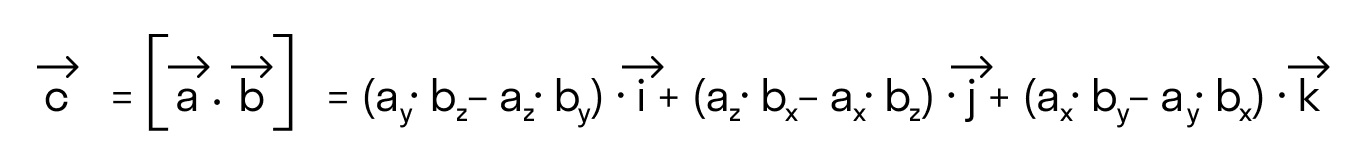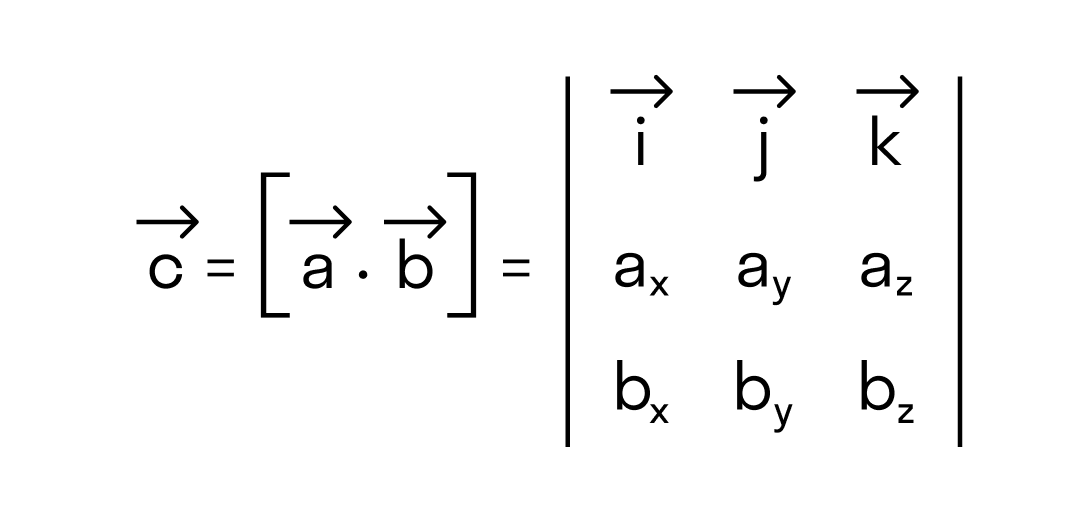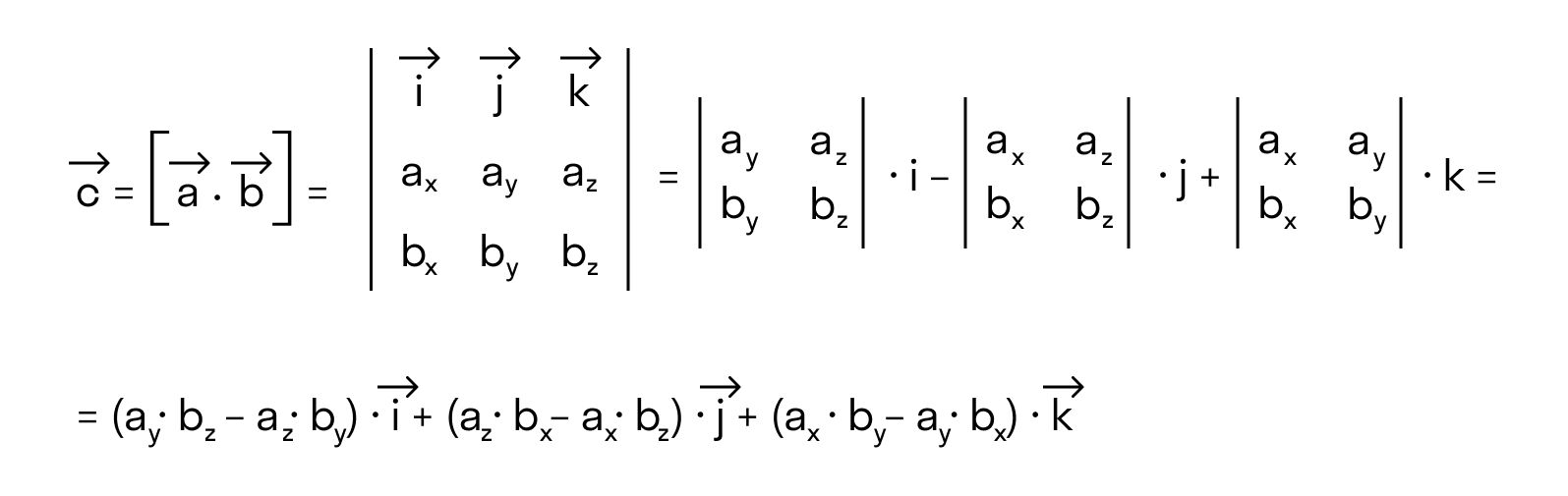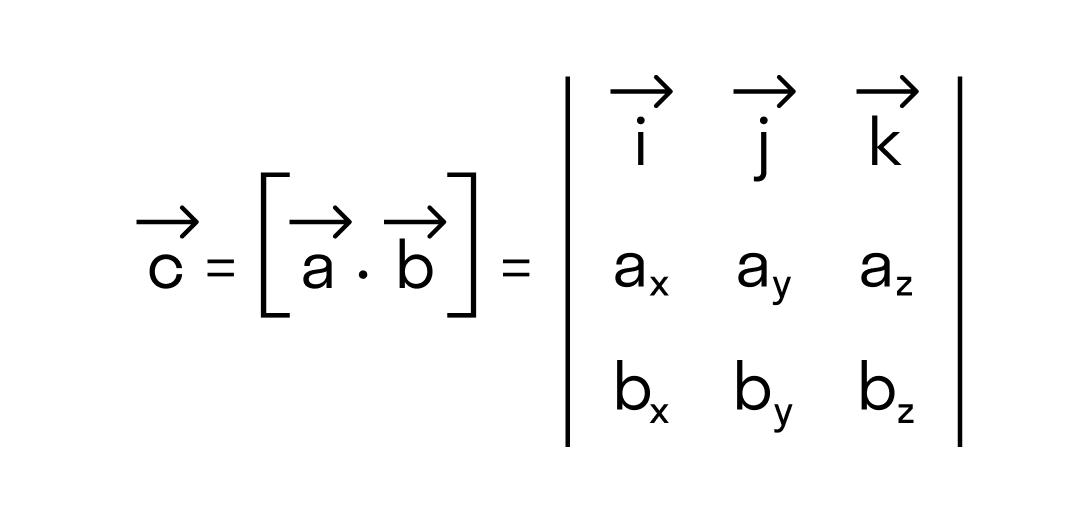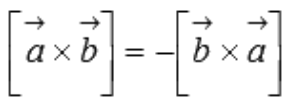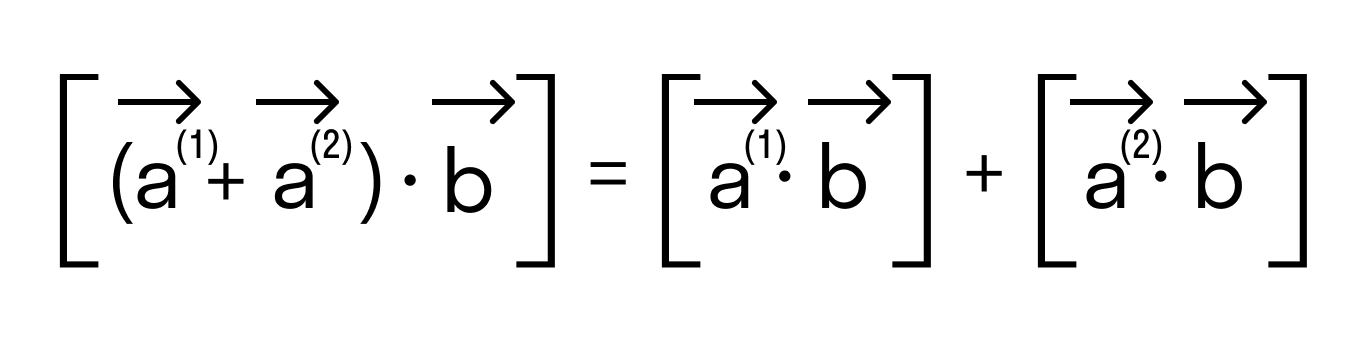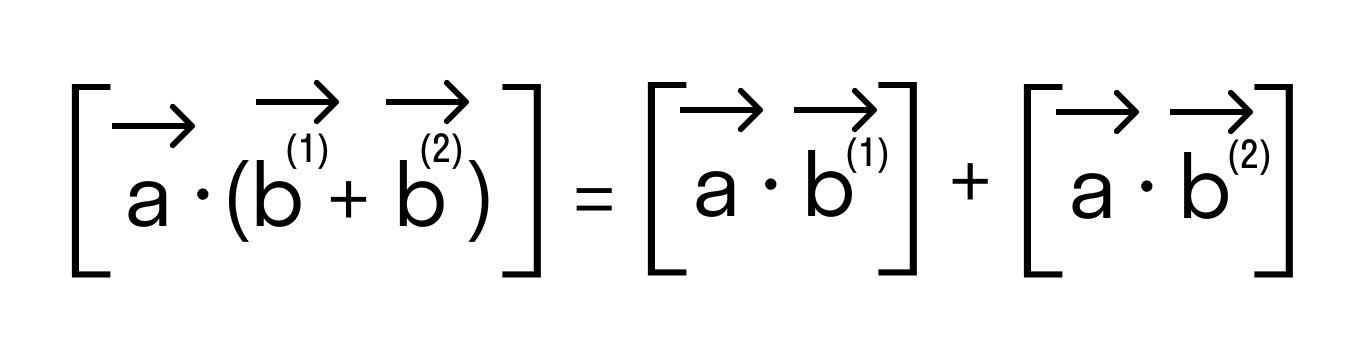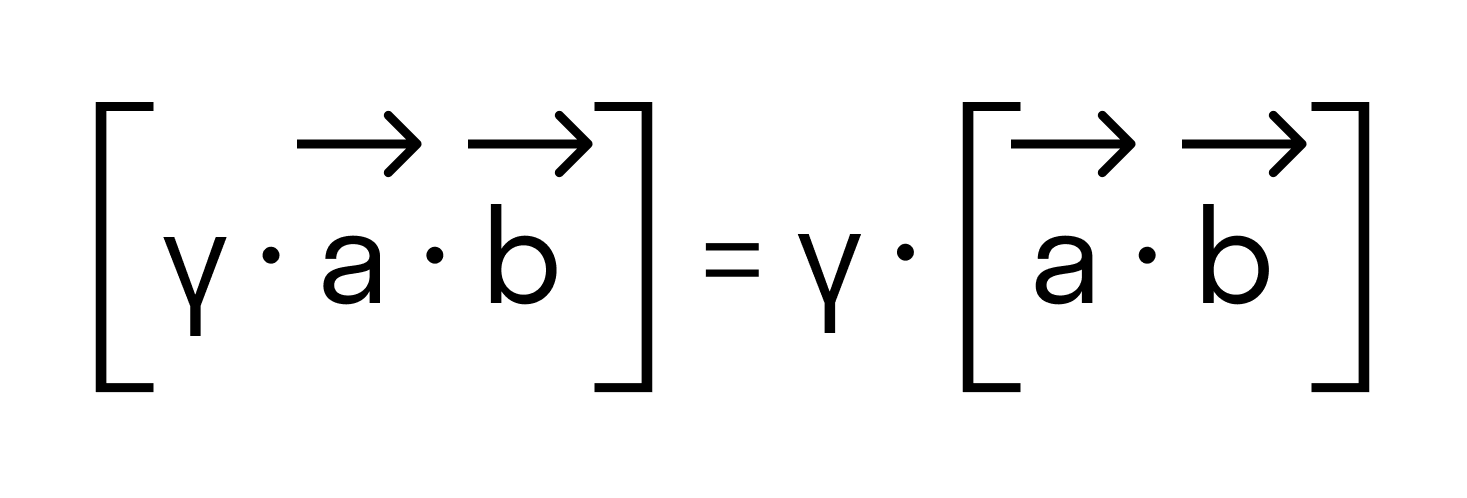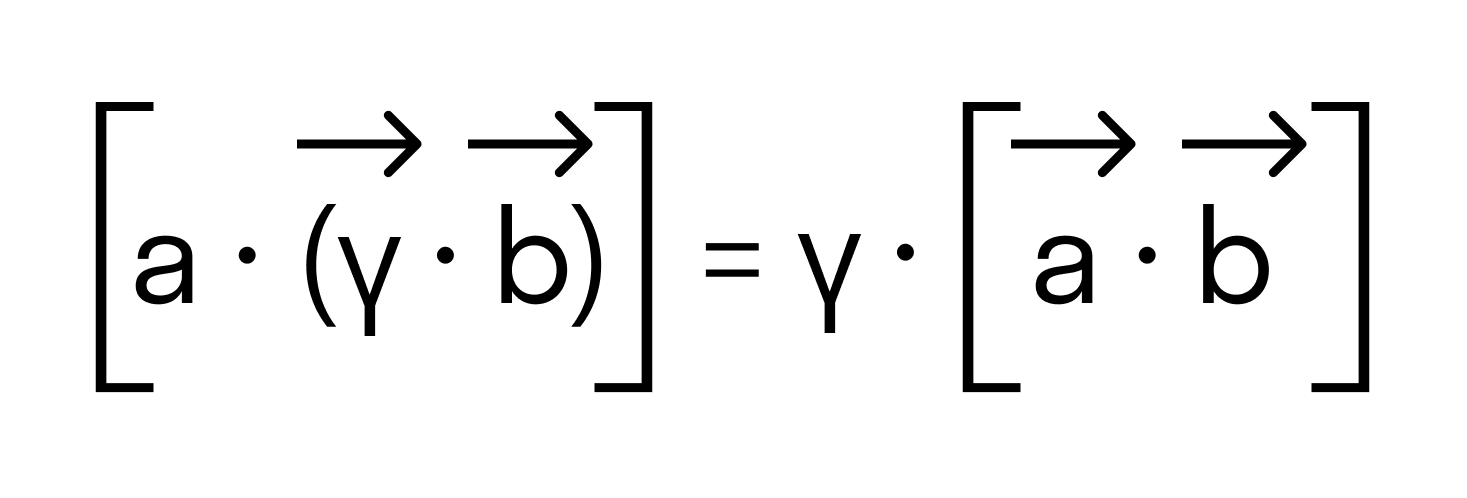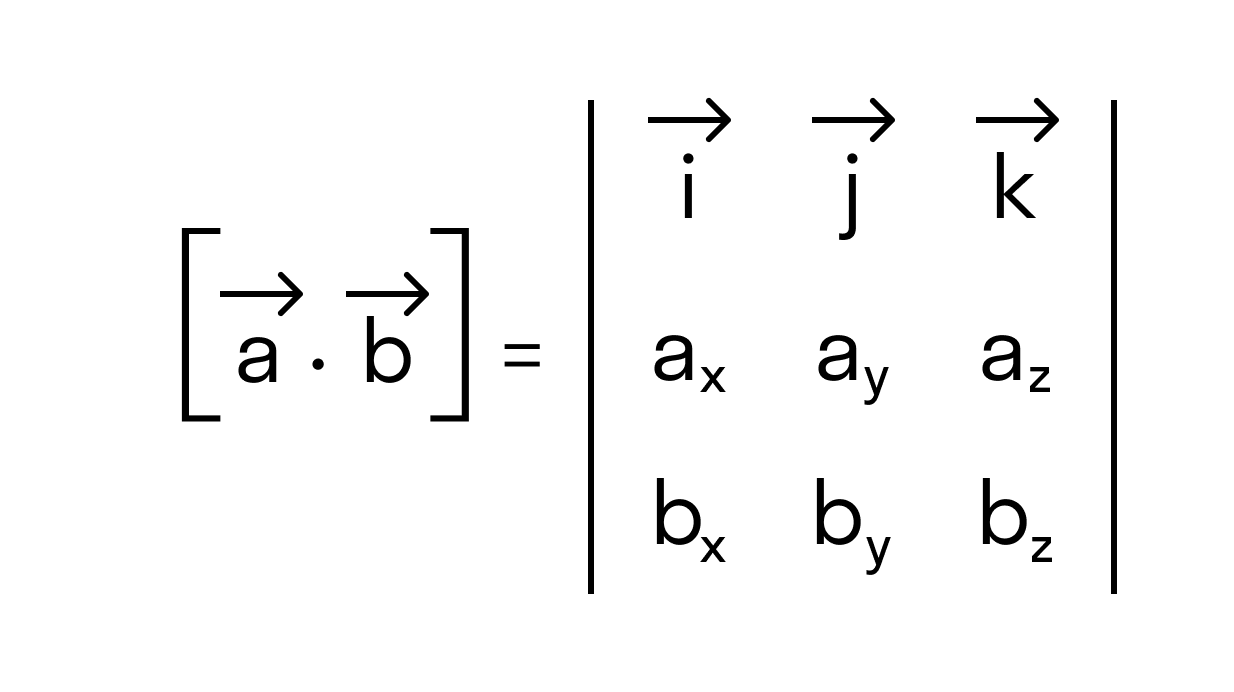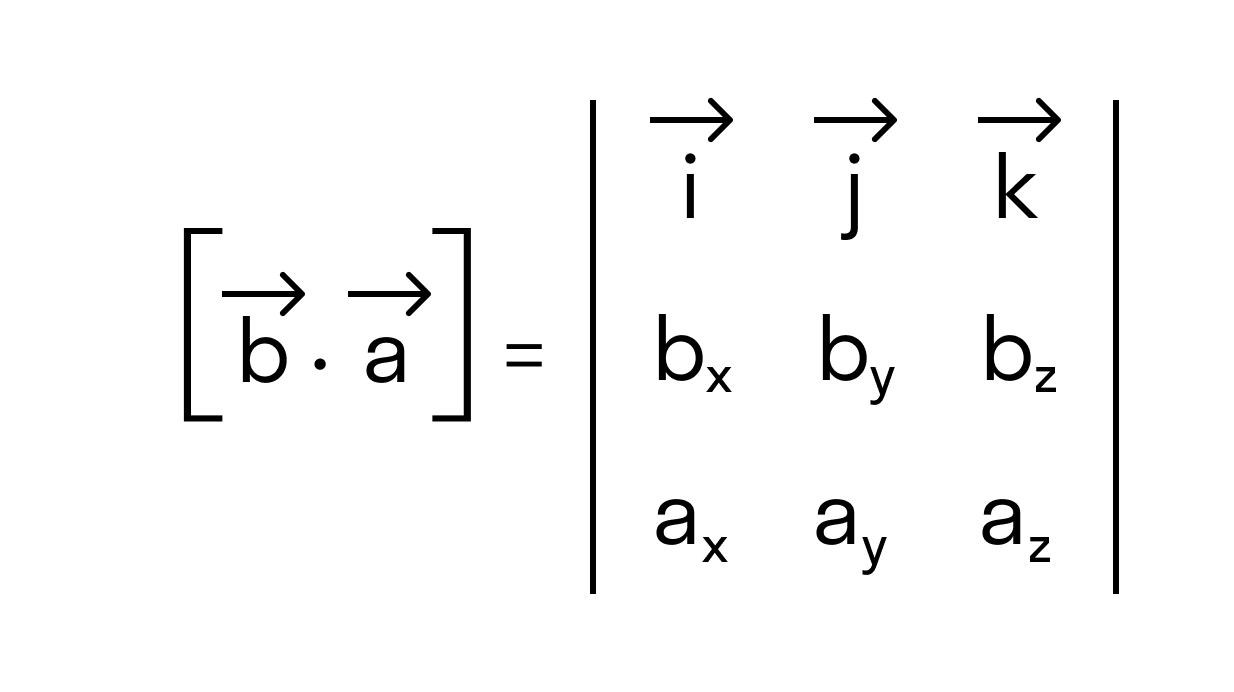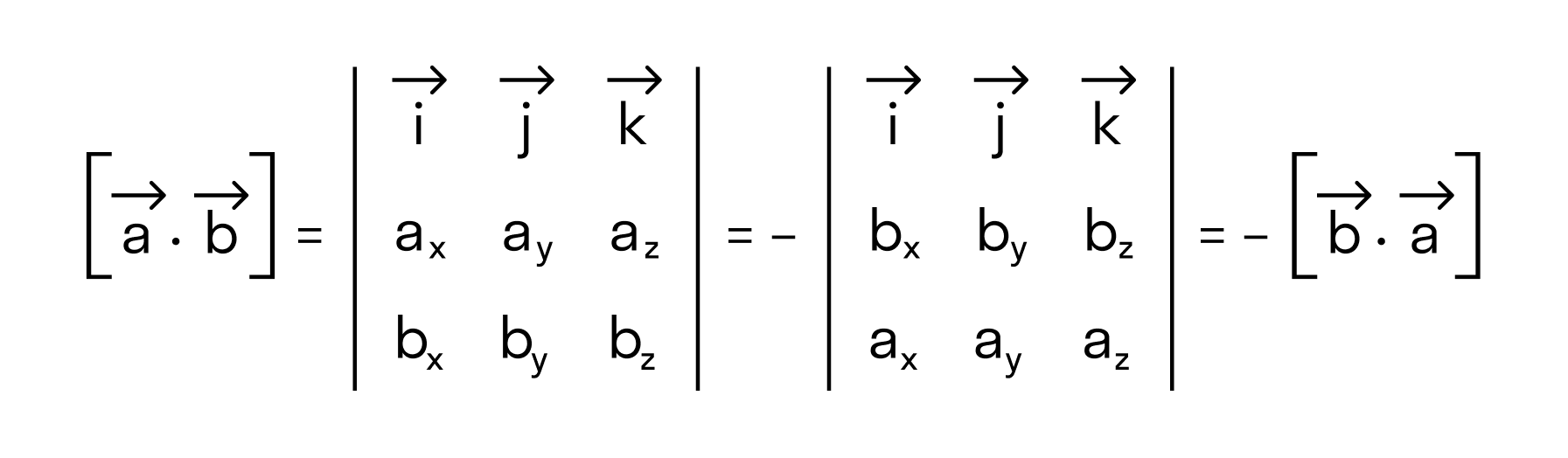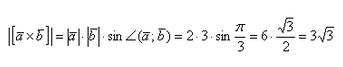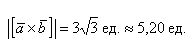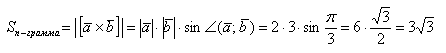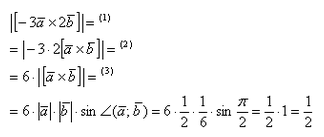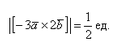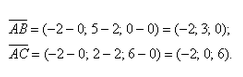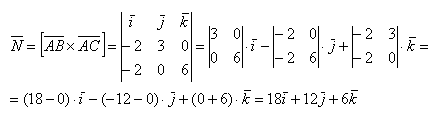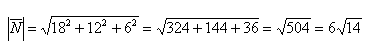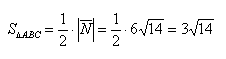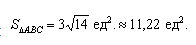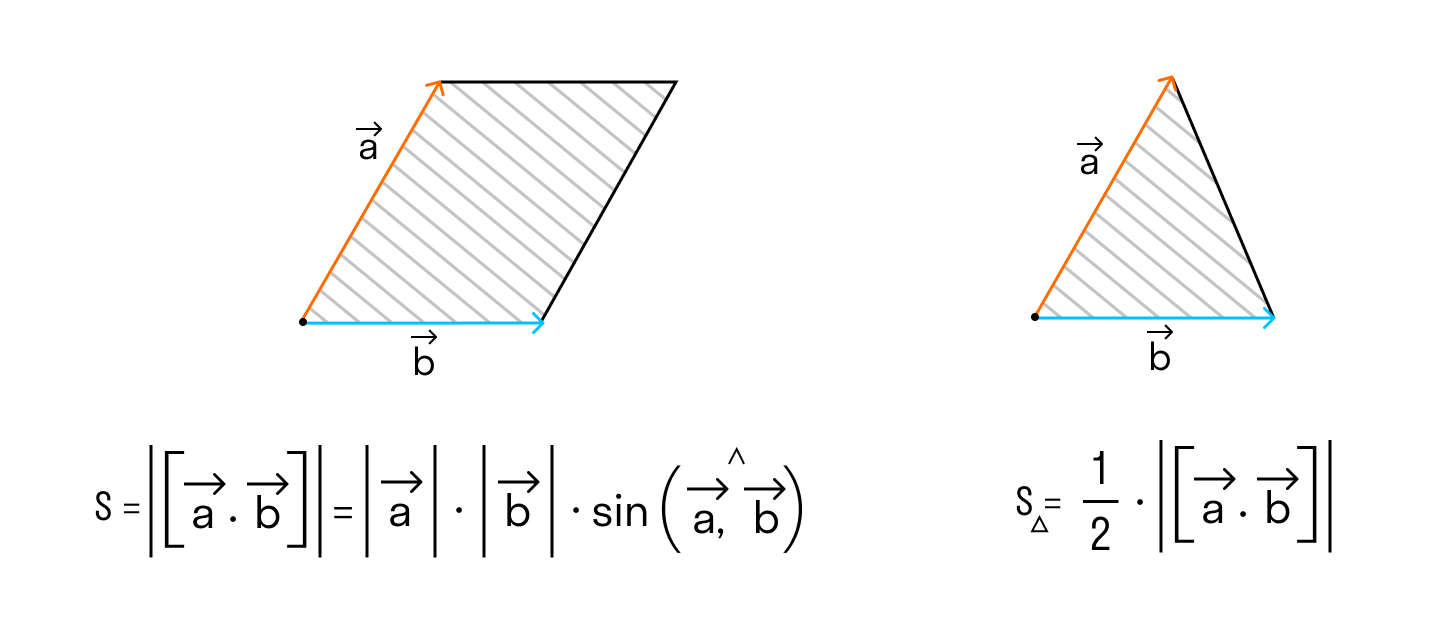О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
- Определение векторного произведения
- Координаты векторного произведения
- Свойства векторного произведения
- Примеры решения задач
- Пример 1
- Пример 2
- Пример 3
- Геометрический смысл векторного произведения
- Физический смысл векторного произведения
- Сложение и вычитание векторов 9 класс
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Описание презентации по отдельным слайдам:
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
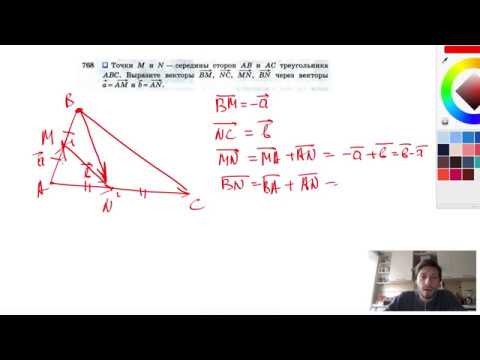
- Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторы ВМ, NC, MN, BN через векторы а = AM и b = AN.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 📺 Видео
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
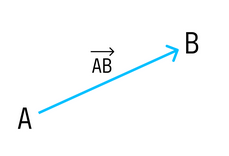
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
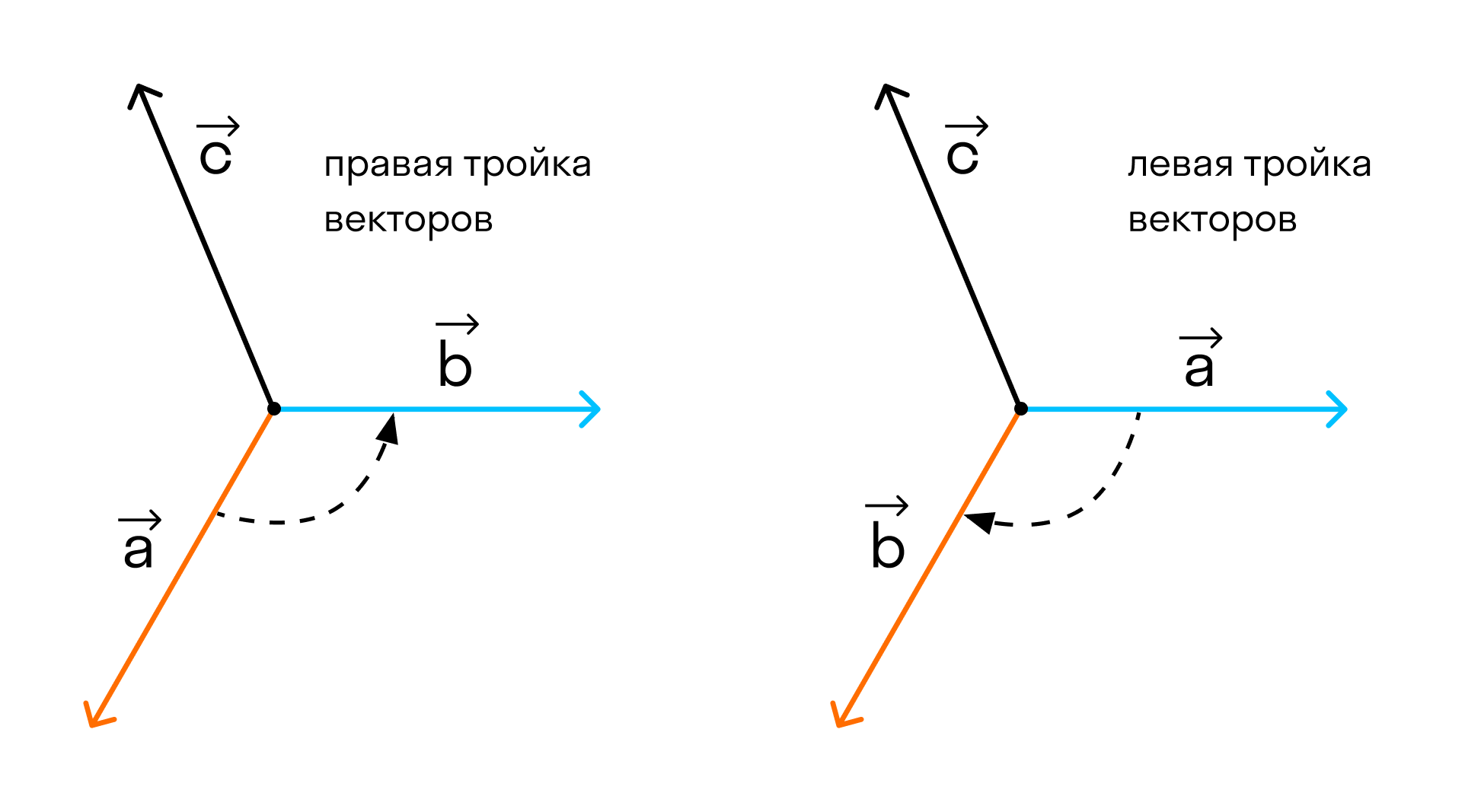
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
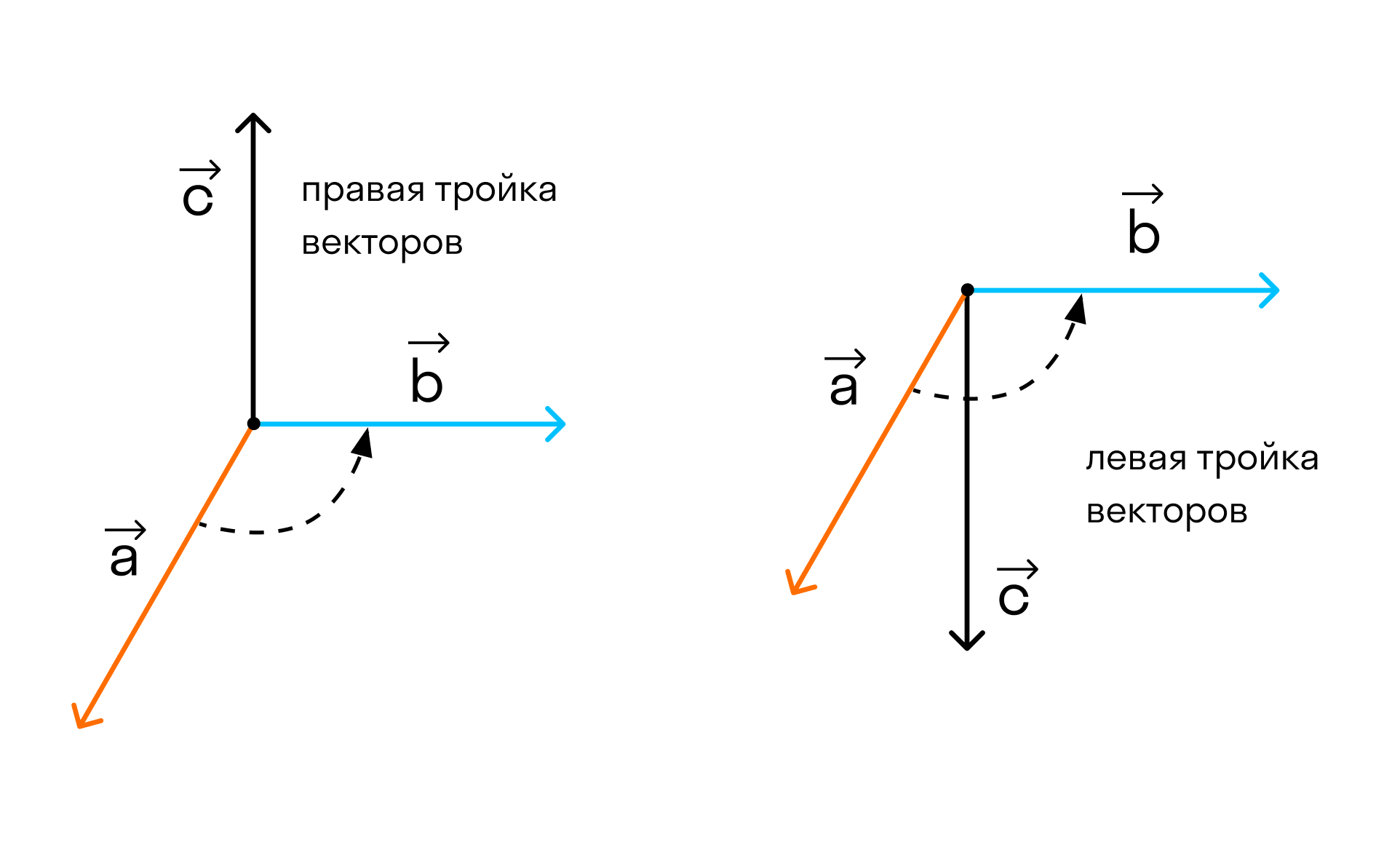
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
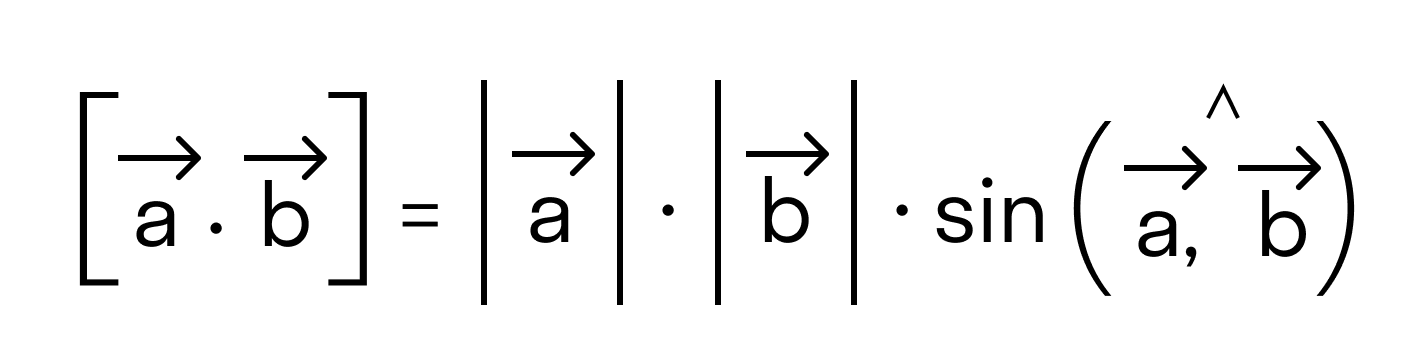
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
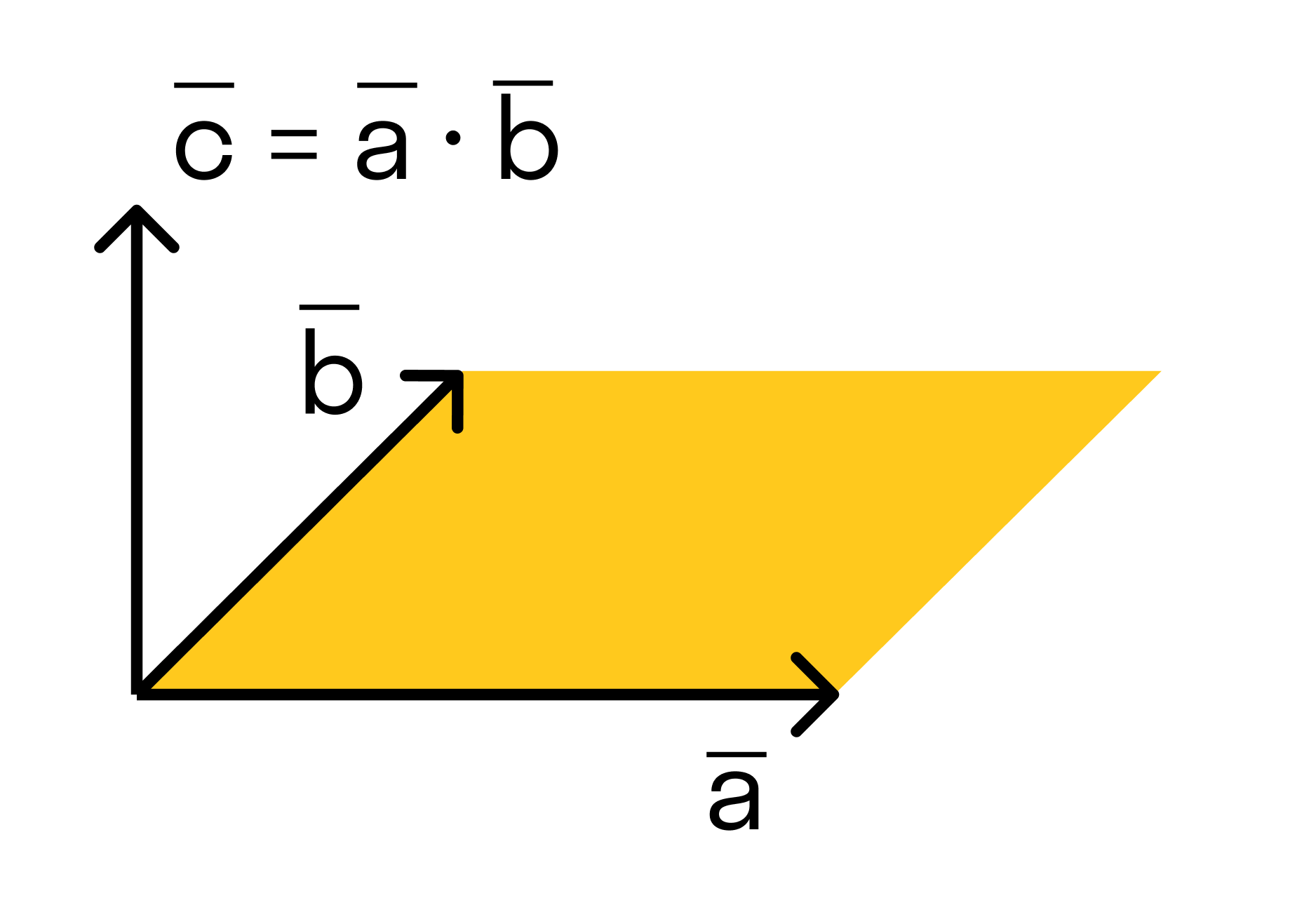
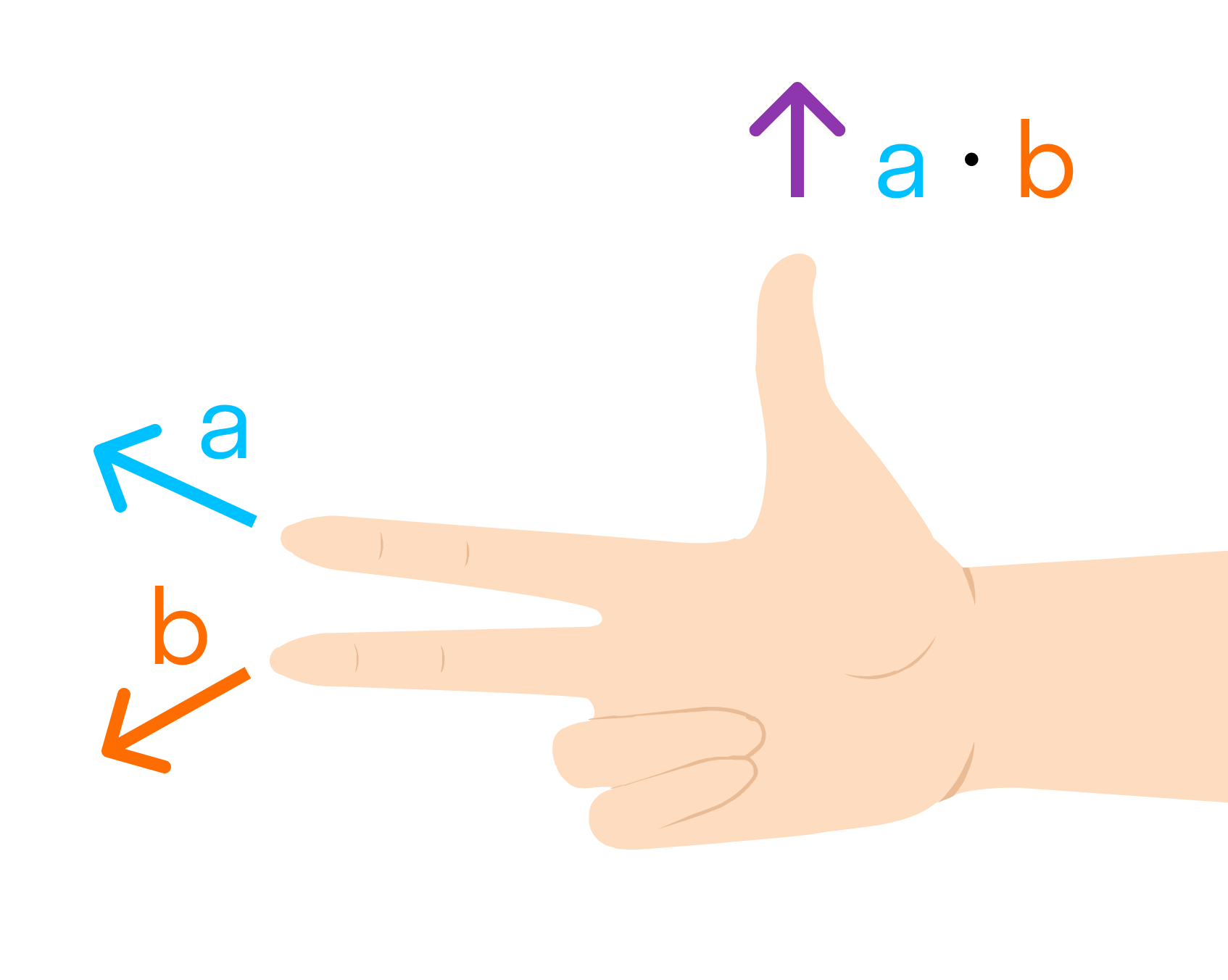
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Видео:8 класс, 42 урок, Откладывание вектора от данной точкиСкачать

Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Видео:№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Видео:Геометрия 9 Откладывание вектора от данной точкиСкачать

Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Видео:№743. Начертите ненулевой вектор a и отметьте на плоскости три точки A, B, C.Скачать
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Видео:81. Откладывание вектора от данной точкиСкачать

Физический смысл векторного произведения
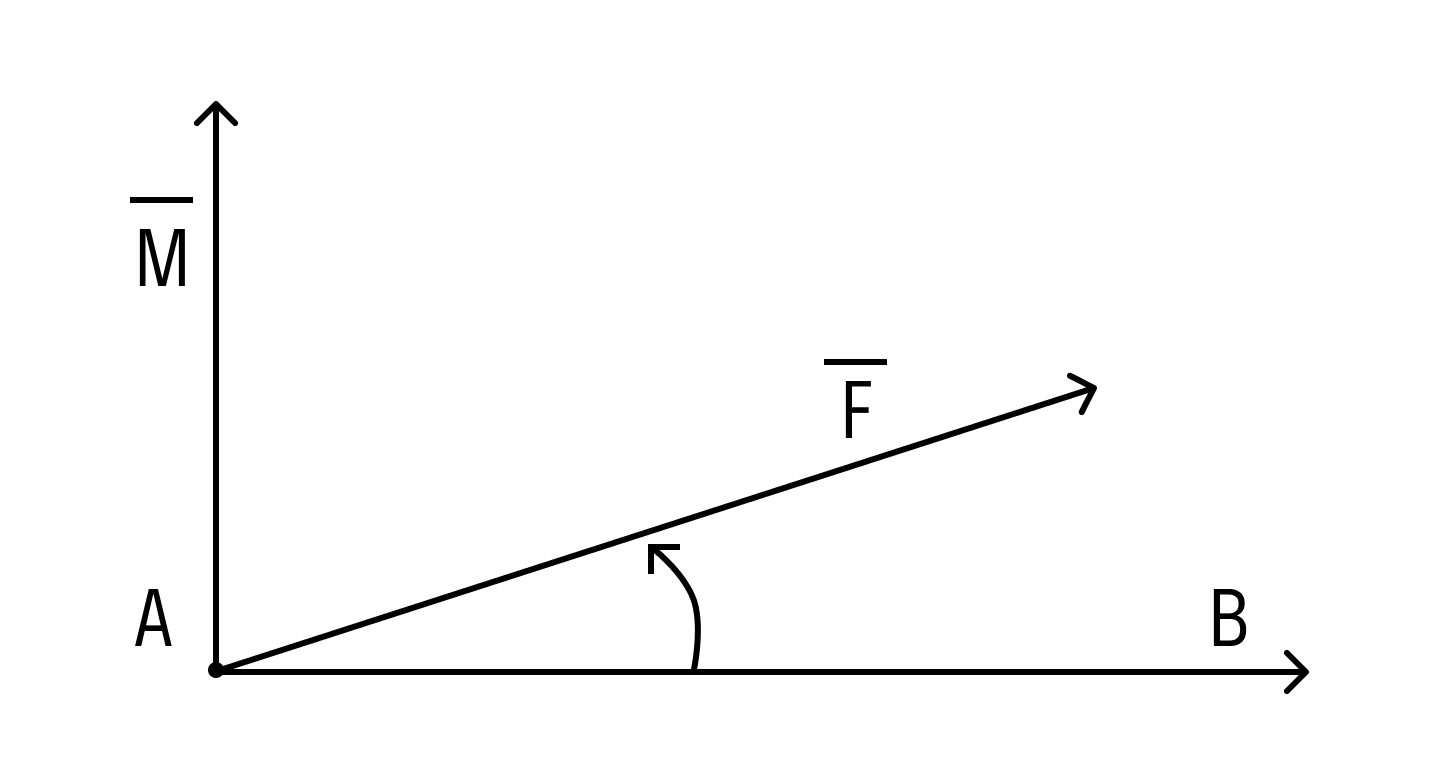
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Видео:№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

Сложение и вычитание векторов 9 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Сложение и вычитание
векторов
Л.С. Атанасян «Геометрия 7-9»
А
В
С
Какая запись является верной?
450
AВ > BC;
AВ > BC
AC = BC ;
AC = BC
Назовите коллинеарные сонаправленные векторы
Назовите коллинеарные противоположнонаправленные векторы
A
B
C
D
N
M
R
E
S
F
H
J
K
L
Z
I
O
P
X
G
Q
V
T
Y
U
Назовите равные векторы
Сложение векторов. Правило треугольника.
a
a
b
b
a +
b
А
В
С
АВ + ВС =
АС
a + 0 = a
!
!
Для любого нулевого вектора справедливо равенство
В1
Докажем, что если при сложении векторов точку А заменить другой точкой А1, то полученный вектор А1С1
будет равен АС. Рассмотрим случай.
a
b
В
b
a
b
a
b
a +
А
С
b
a +
С1
А1
АВВ1А1 – параллелограмм
ВСС1В1 – параллелограмм
АСС1А1 – параллелограмм
= OK
АВ + ВС =
Правило треугольника.
АС
АО + ОР =
АР
MN + NR =
MR
MK + KM =
MM = 0
MK + OM =
OM + MK
= KE
АS + SС =
АС
NM + ML =
NL
RP + PR =
RR = 0
ZK + KZ =
ZZ = 0
DE + KD =
KD + DE =
Правило треугольника.
АС =
АВ + ВС
OB + ВN
ON =
AR + RS
AS =
XK + KH
XH =
MA + AD
MD =
OF + FP
OP =
ON + NВ
OB =
RS + SA
RA =
KH + HX
KX =
AM + MD
AD =
FP + PO
FO =
По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получается
a
b
a +
b
a
b
a +
b
Законы сложения векторов
Для любых векторов справедливы равенства:
a, b, c
1
2
a + b = b + a
переместительный закон
сочетательный закон
(a + b) + c = a + (b + c)
!
!
Теорема
Рассмотрим случай, когда векторы и не коллинеарны.
b
a
1
1
2
9
6
12
11
10
8
7
4
5
3
При доказательстве свойства 10 мы обосновали правило параллелограмма сложения неколлинеарных векторов.
Чтобы применить правило параллелограмма, надо отложить векторы от одной точки, как стрелки часов.
Сложение векторов.
Правило многоугольника.
= АO
АВ + ВС + СD + DO
a
c
n
m
c
m
n
a+c+m+n
a
Правило многоугольника можно сформулировать также следующим образом: если А1, А2, …, Аn – произвольные точки плоскости, то
= А1An
А1А2 + А2А3 + … + Аn-1An
А2
А3
А4
А5
А6
А7
А1
!
Если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.
a1+a2+a3+a4+a5
= 0
a1
a1
a2
a2
a3
a4
a5
a3
a4
a5
Вектор называется противоположным
вектору , если векторы и имеют равные
длины и противоположно направлены.
a1
b
-b
a
a
a1
-b
b
Вектор , противоположный вектору
А
В
А
В
Вектор ВА, противоположный
вектору АВ
a + (-a) = 0
ВА = – АВ
a
a1
a = a1 ;
a a1
a
b
№ 766 На рисунке изображены векторы
ХУ. Представьте вектор ХУ в виде суммы остальных или им
Вычитание векторов.
MF — SF =
MF + FS
= MS
RO — RM =
RO + MR
= MR + RO
MD — SD =
MD + DS
= MS
— OS — ST =
SO + TS
= TS + SO
RO — AO =
RO + OA
= RA
RO — RO =
RO + OR
= RR
= 0
= TO
= MO
№ 768 Точки М и N – середины сторон АВ и АС
треугольника АВС. Выразите векторы ВМ, NC, MN, BN
( )
Найдите
АВ + AD – DC – OD
ABCD — прямоугольник
А
B
C
D
АВ + AD – DC – OD
= АС – DC – OD
= АС + CD + DO
= АО
О
3
4
5
АВ + ВС =
АО + ОР =
MN + NR =
MK + KM =
MK + OM =
АS + SС =
NM + ML =
RP + PR =
ZK + KZ =
DE + KD =
ON =
AS =
XH =
MD =
OP =
OB =
RA =
KX =
AD =
FO =
Курс повышения квалификации
Охрана труда
- Сейчас обучается 92 человека из 43 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 348 человек из 65 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 221 человек из 52 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 511 428 материалов в базе
Другие материалы
- 03.01.2021
- 219
- 0
- 03.01.2021
- 385
- 3
- 03.01.2021
- 556
- 5
- 03.01.2021
- 381
- 0
- 03.01.2021
- 300
- 0
- 03.01.2021
- 301
- 0
- 03.01.2021
- 405
- 1
- 03.01.2021
- 730
- 4
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 02.04.2020 1523
- PPTX 2.1 мбайт
- 91 скачивание
- Рейтинг: 3 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Винокурова Надежда Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 25278
- Всего материалов: 240
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:№767. Дан треугольник ABC. Выразите через векторы а=АВ и b=АС следующие векторы:Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу
Время чтения: 1 минута
В Петербурге введут новые COVID-ограничения для несовершеннолетних
Время чтения: 2 минуты
В Тюменской области школы и колледжи перевели на дистанционное обучение
Время чтения: 1 минута
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Петербурге открыли памятник работавшим во время блокады учителям
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Откладывание вектора от данной точки | Геометрия 7-9 класс #78 | ИнфоурокСкачать

Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторы ВМ, NC, MN, BN через векторы а = AM и b = AN.
Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Ваш ответ
Видео:№776. Начертите два неколлинеарных вектора х и у и постройте векторы: a) x+2y; б) ½y + х; в) 3x+½yСкачать

решение вопроса
Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,989
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
📺 Видео
№778. Начертите попарно неколлинеарные векторы а, b и c. Постройте векторы:Скачать

10 класс, 43 урок, Компланарные векторыСкачать

№362. Точка К — середина ребра ВС тетраэдра ABCD. Разложите вектор DK по векторамСкачать

2 урок. Сложение и вычитание векторов | Геометрия. 9 классСкачать

10.04 9a Откладывание вектора от данной точкиСкачать

№775. Начертите два неколлинеарных вектора р и q , начала которых не совпадаютСкачать