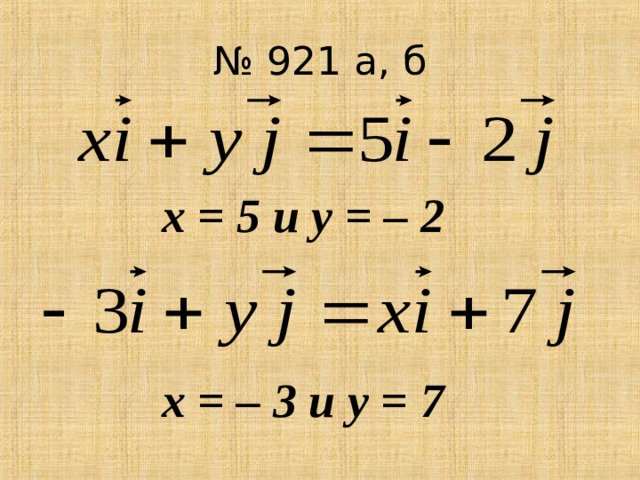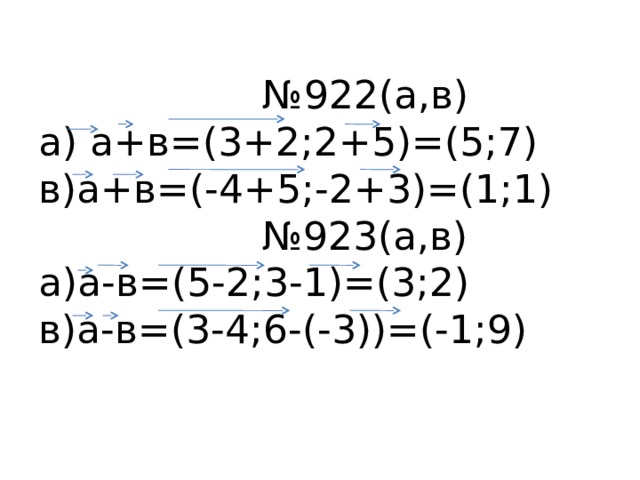Координатная плоскость состоит из двух взаимно перпендикулярных координатных прямых. Началом отсчета на обеих прямых принято считать точку их пересечения (точку $О$). Горизонтальная ось $О_х$ называется абсциссой, вертикальная ось $О_у$ — ординатой.
У каждой точки на плоскости есть две координаты, в скобках на первом месте всегда стоит координата $Х$, на втором $Y$, например $М(2;3)$ – читается: точка $М$ имеет координату $х=2$, координату $у=3$. Симметрия точек относительно осей координат:
- У точек, симметричных относительно оси $О_х$ абсциссы совпадают, а ординаты являются противоположными числами.
- У точек, симметричных относительно оси $О_у$ ординаты совпадают, а абсциссы являются противоположными числами.
Векторы и отрезки в координатах:
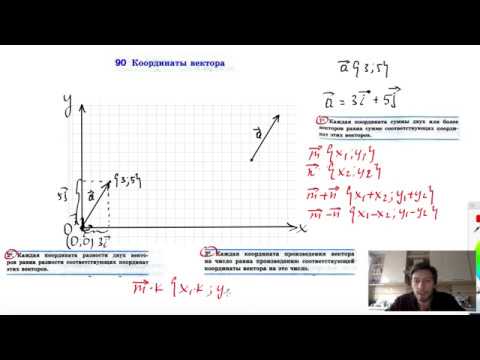
1. Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.
2. Координаты середины отрезка (вектора) равны среднему арифметическому координат его концов.
Найдите абсциссу середины отрезка, соединяющего точки $В(2;8)$ и $A(6;4)$.
Пусть точка $М$ – середина отрезка $ВА$. Чтобы найти абсциссу данной точки, надо найти среднее арифметическое абсцисс концов отрезка:
3. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
4. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
5. Длинна отрезка или расстояние между двумя точками $M_1(x_1;y_1)$ и $M_2(x_2; y_2)$ находится по формуле
Найдите длину отрезка, соединяющего точки $A(5,-8)$ и $C(-3,-2)$.
Применим формулу нахождения длины отрезка
В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Действия с координатами векторов. 1. Координаты равных векторов_(это следует из 2. Каждая координата суммы двух или
Видео:Геометрия, 9 класс, Правила нахождения координат суммы, разности векторов, произведенияСкачать

Ваш ответ
Видео:Координаты вектора. 9 класс.Скачать

решение вопроса
Видео:Сложение, вычитание, умножение на число векторов через координату. 9 класс.Скачать

Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,962
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Координаты вектора в пространстве. 11 класс.Скачать

Координаты вектора
Нахождение координат вектора.
Просмотр содержимого документа
«Координаты вектора»

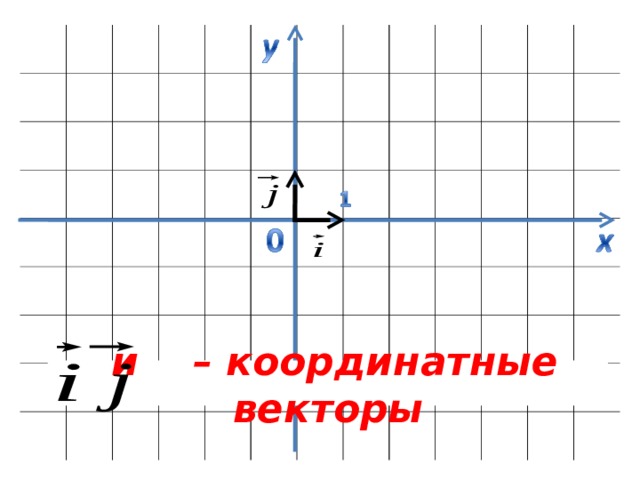
и – координатные векторы
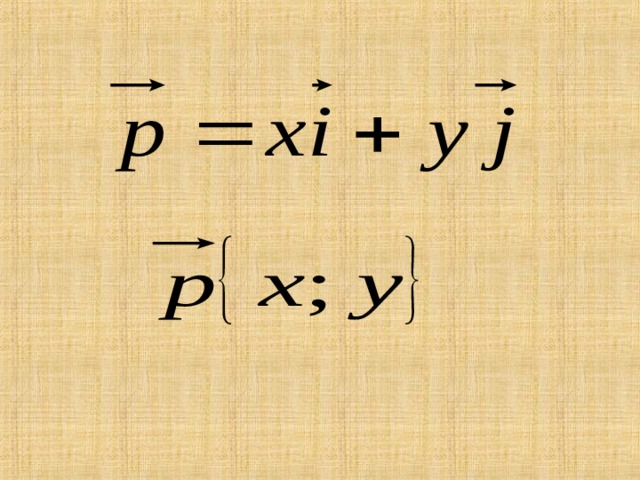
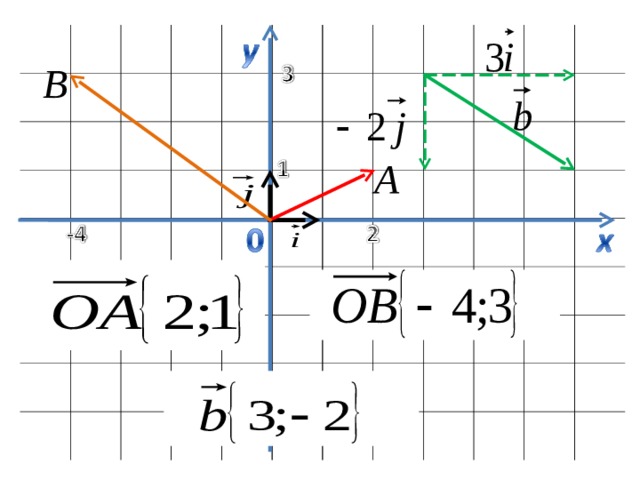
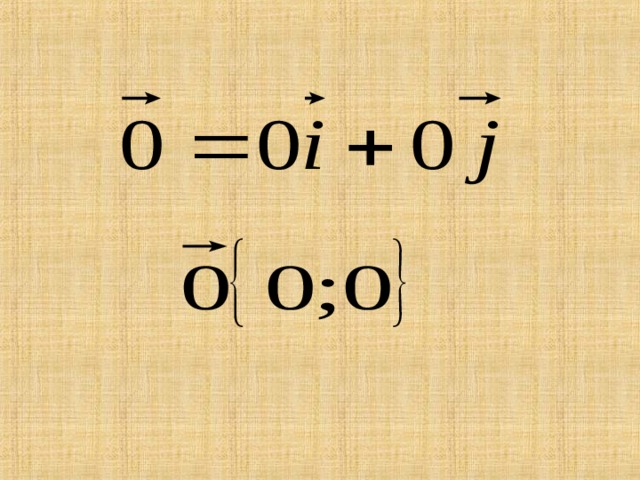
Координаты равных векторов соответственно равны
1 0 . Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Доказать: Координаты вектора
Доказательство: Так как , то
Отсюда следует, что координаты суммы двух векторов равны сумме соответствующих координат этих векторов.
2 0 . Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.
3 0 . Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Найдём координаты вектора
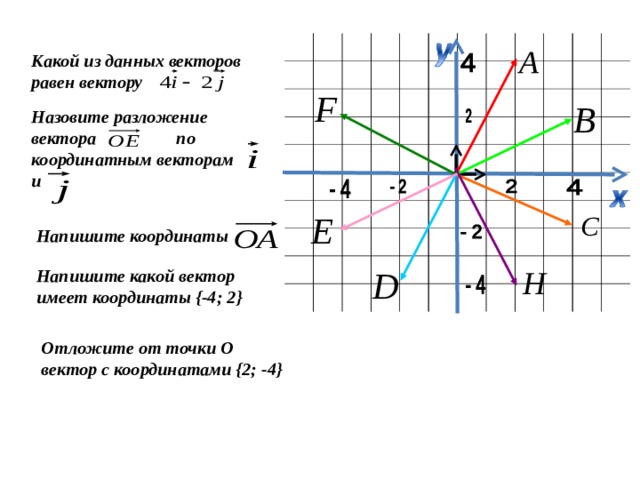
Какой из данных векторов равен вектору
Назовите разложение вектора по координатным векторам и
Найти координаты векторов:
Домашнее задание: п. 87, вопросы 7 – 8. № 918, 919,922(б,г).
🌟 Видео
90. Координаты вектораСкачать
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

9 класс, 2 урок, Координаты вектораСкачать

Разложение вектора по двум неколлинеарным векторам. Урок 4. Геометрия 9 классСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Координаты Векторов. Практика. Урок 2. Геометрия 11 классСкачать

№ 406 - Геометрия 10-11 класс АтанасянСкачать

Геометрия 9 класс (Урок№8 - Связь между координатами вектора и координатами его начала и конца.)Скачать

Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в координатахСкачать

Координаты вектора | Геометрия 7-9 класс #86 | ИнфоурокСкачать

Геометрия 11 класс (Урок№1 - Координаты в пространстве. Система координат.)Скачать

Координаты вектора.Скачать

11 класс, 2 урок, Координаты вектораСкачать