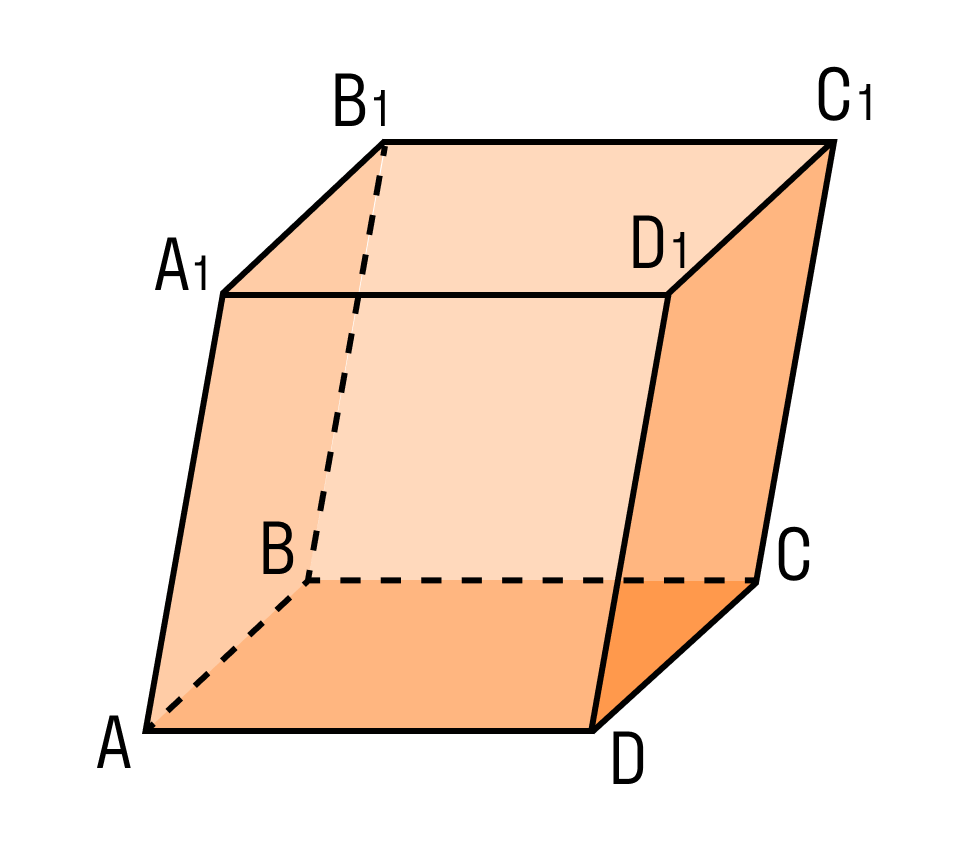
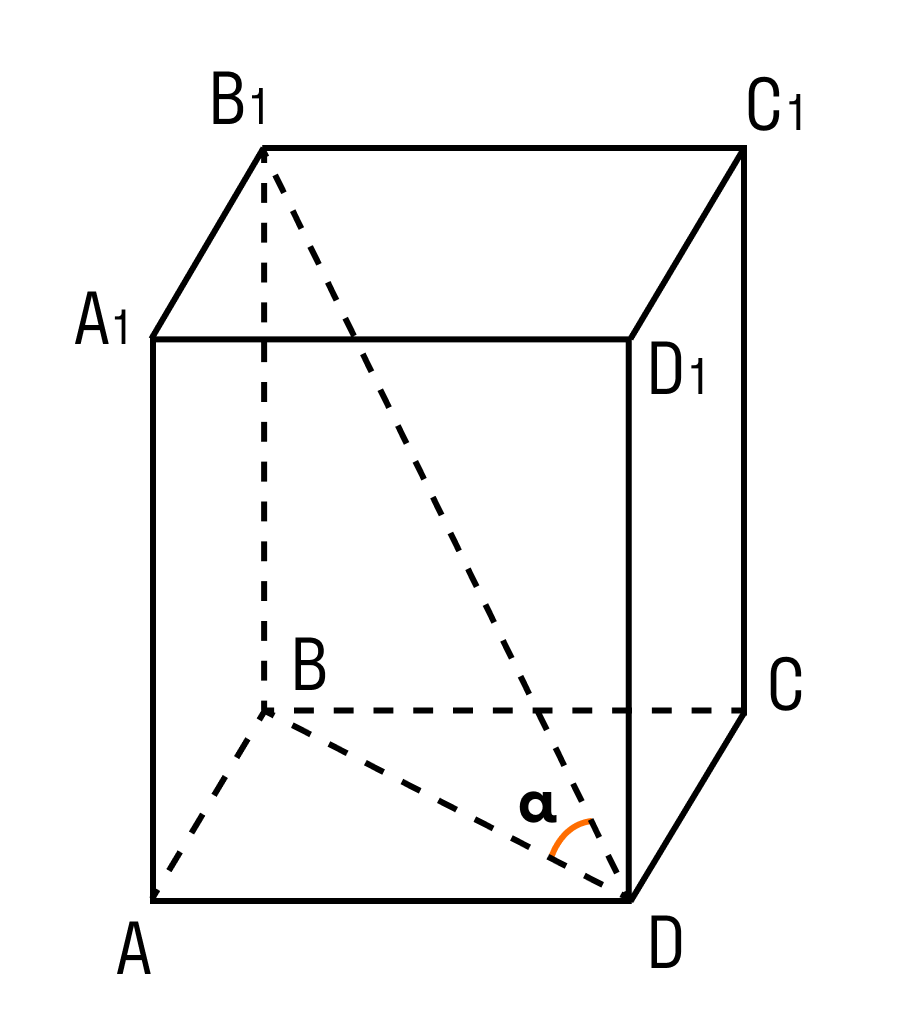
Наклонный параллелепипед в основании которого ромб свойства все грани одинаковые четырехугольники

Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, относительно оснований, под не прямым углом.

Наклонная призма эквивалентна такой прямой призме, у которой основание равняется перпендикулярному сечению наклонной призмы, а высота — ее боковому ребру.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Свойства наклонного параллелепипеда.

1) Каждая его грань – параллелограмм, а противолежащие грани — одинаковые параллелограммы.

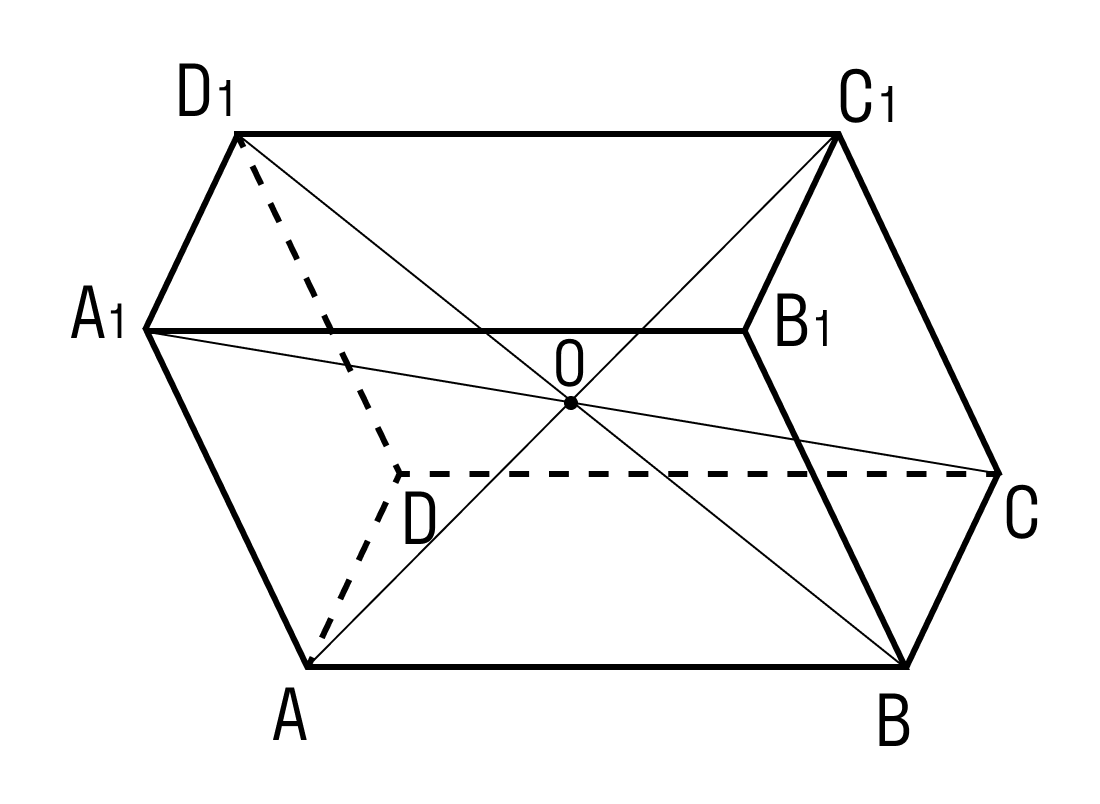
2) Диагонали параллелепипеда пересекаются в одной точке и делятся в этой точкой на две равные части.

3) Все параллелепипеды состоят из 6-ти одинаковых по объему треугольных пирамид.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Объем наклонного параллелепипеда.

где S_осн — площадь основания, h – высота.

Объем параллелепипеда можно найти как произведение площади поперечного сечения на боковое ребро:

Кроме того, объем параллелепипеда определяют как произведение площади основания на высоту. Доказывается так, что объем наклонного параллелепипеда равняется объему прямоугольного параллелепипеда с такой же площадью основания и высотой, как и у наклонного параллелепипеда.

Видео:№295. Основанием наклонного параллелепипеда ABCDA1B1C1D1 является ромб. Боковое ребро СС1 составляетСкачать

Что такое параллелепипед: определение, элементы, виды, свойства

В данной публикации мы рассмотрим определение, элементы, виды и основные свойства параллелепипеда, в т.ч. прямоугольного. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Определение параллелепипеда

Параллелепипед – это геометрическая фигура в пространстве; шестигранник, гранями которого являются параллелограммы. Фигура имеет 12 ребер и 6 граней.

Параллелепипед – это разновидность призмы с параллелограммом в качестве оснований. Основные элементы фигуры те же, что и у призмы.

Примечание: Формулы для расчета площади поверхности (для прямоугольной фигуры) и объема параллелепипеда представлены в отдельных публикациях.

Видео:Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

Виды параллелепипедов

1. Прямой параллелепипед – боковые грани фигуры перпендикулярны ее основаниям и являются прямоугольниками.
2. Прямой параллелепипед может быть прямоугольным – основаниями являются прямоугольники.
3. Наклонный параллелепипед – боковые грани не перпендикулярны основаниям.
4. Куб – все грани фигуры являются равными квадратами.
5. Если все грани параллелепипеда – это одинаковые ромбы, он называется ромбоэдром.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Свойства параллелепипеда

1. Противоположные грани параллелепипеда взаимно параллельны и являются равными параллелограммами.

2. Все диагонали параллелепипеда пересекаются в одной точке и в ней делятся пополам.

3. Квадрат диагонали (d) прямоугольного параллелепипеда равен сумме квадратов трех его измерений: длины (a), ширины (b) и высоты (c).

d 2 = a 2 + b 2 + c 2

Примечание: к параллелепипеду, также, применимы свойства призмы.

Видео:Ромб. 8 класс.Скачать

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Видео:№220. Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высотаСкачать

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда
  Sб = Ро*h
  Ро — периметр основания
  h — высота
• Площадь полной поверхности прямого параллелепипеда
  Sп = Sб+2Sо
  Sо — площадь основания
• Объем прямого параллелепипеда
  V = Sо*h

Видео:Гранью параллелепипеда является ромб со стороной 1 и острым ....8 ЗАДАНИЕ ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬСкачать

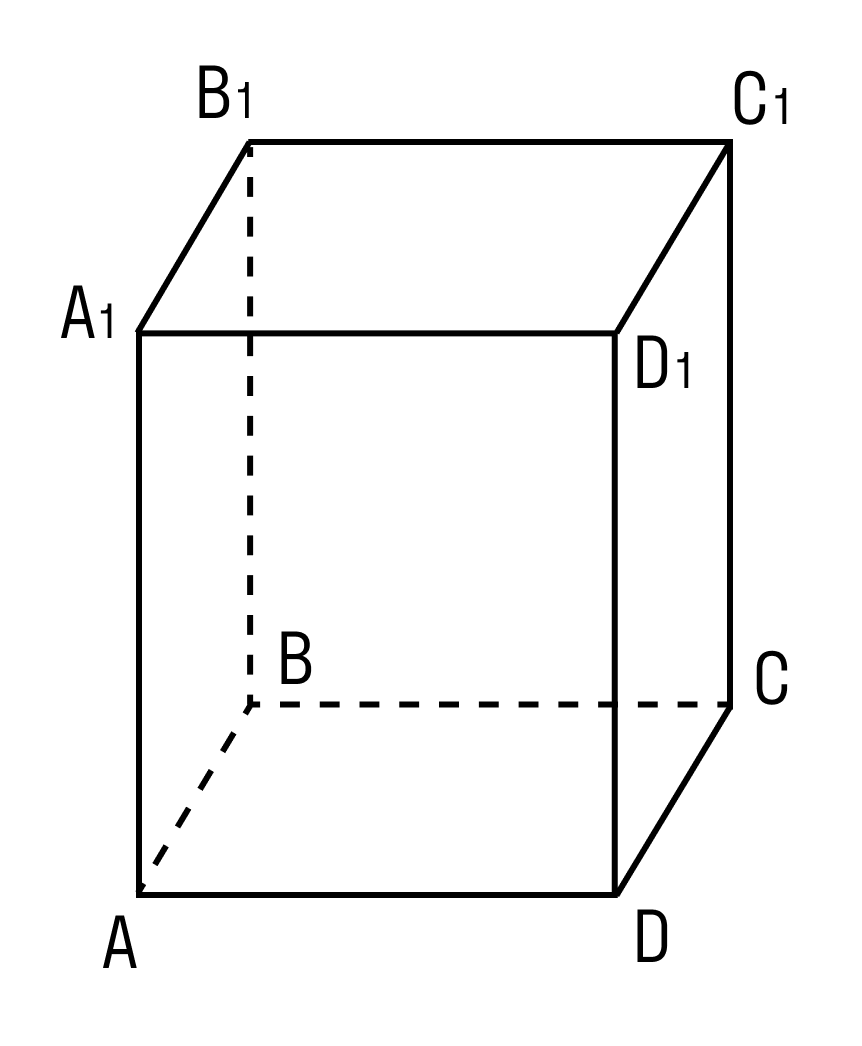
Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Видео:Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

• Объем прямоугольного параллелепипеда
  V = a · b · h
  a — длина, b — ширина, h — высота
• Площадь боковой поверхности
  Sбок = Pосн·c=2(a+b)·c
  Pосн — периметр основания, с — боковое ребро
• Площадь поверхности
  Sп.п = 2(ab+bc+ac)

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

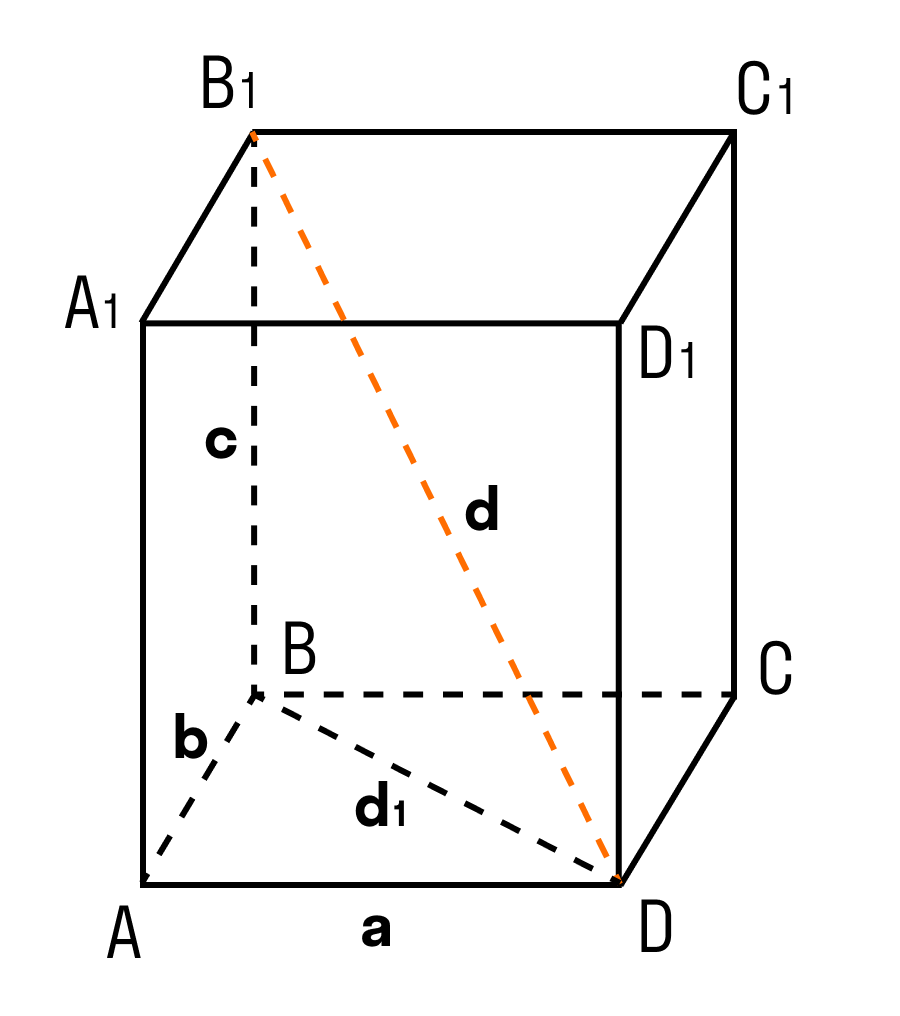
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Видео:Ромб, признаки. 8 класс.Скачать

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

1. В кубе 6 граней, каждая грань куба — квадрат.
2. Противолежащие грани параллельны друг другу.
3. Все углы куба, образованные двумя гранями, равны 90°.
4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5. Диагонали куба равны.
6. Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a
  V = a3
• Площадь поверхности куба
  S = 6a2
• Периметр куба
  P = 12a

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

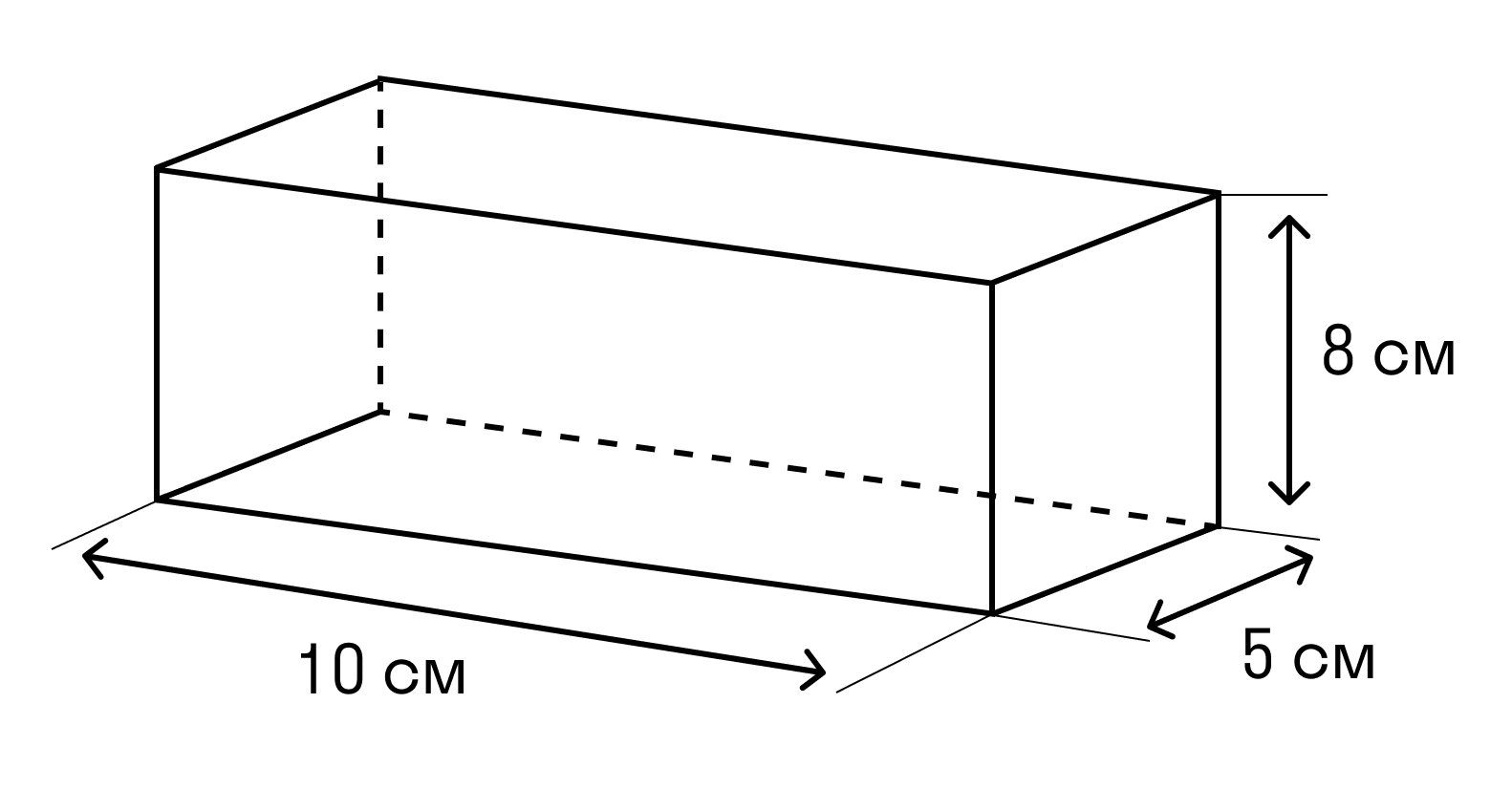
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

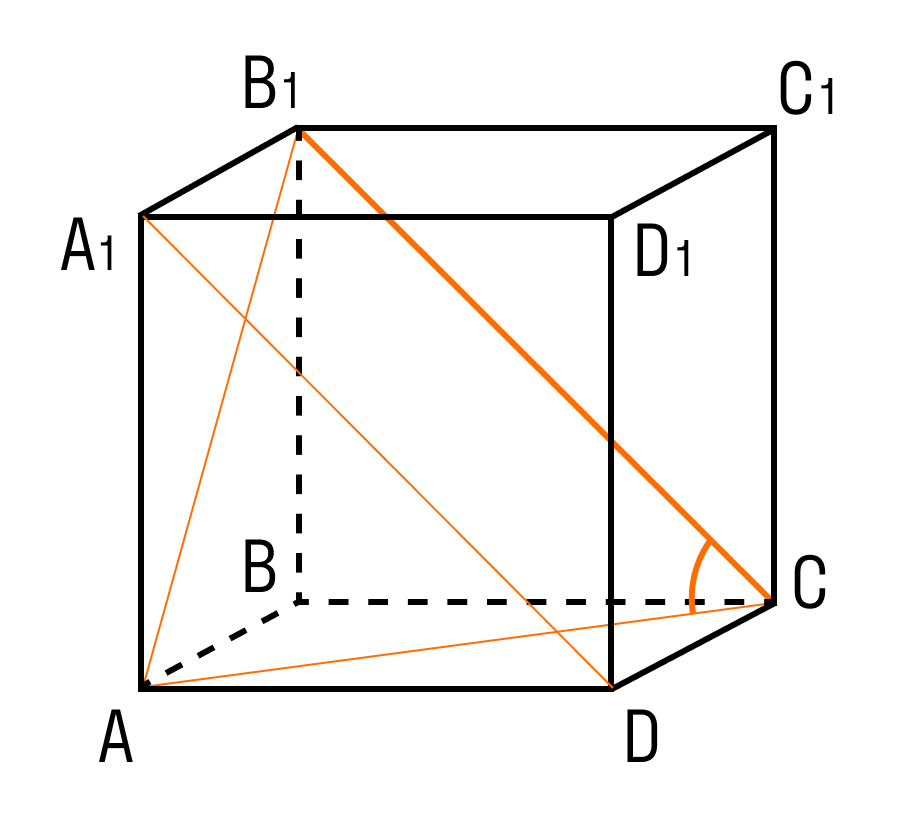
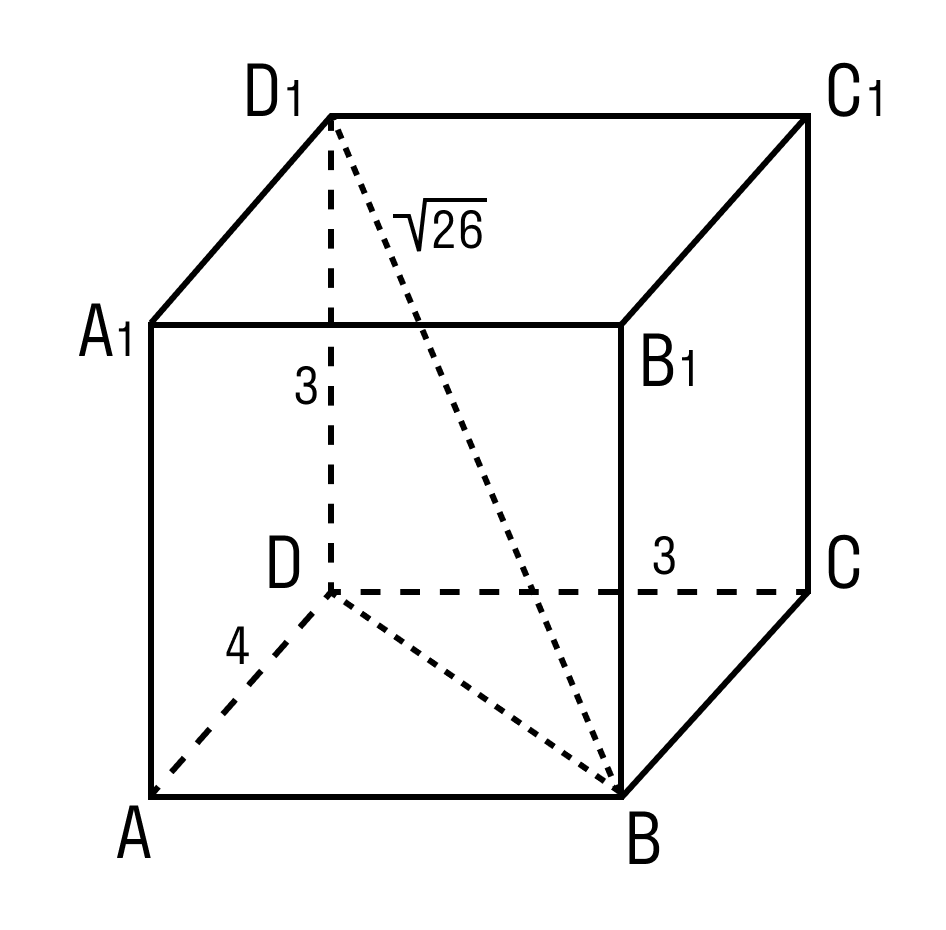
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

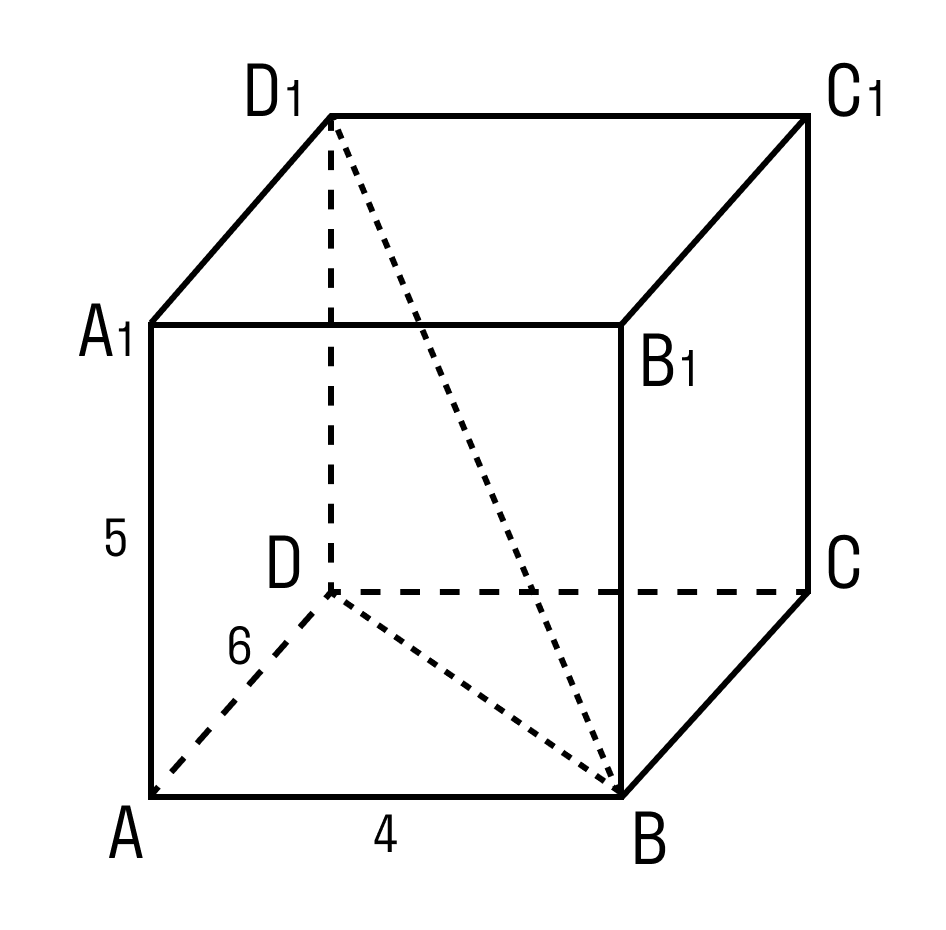
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Видео:основании прямого параллелепипеда лежит ромбСкачать

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

🎬 Видео

8 класс. Геометрия. Прямоугольник Ромб Квадрат Трапеция. Свойства и признаки. Решения задач. Урок #2Скачать

10 класс, 24 урок, Прямоугольный параллелепипедСкачать

Геометрия Доказательство Диагонали ромба перпендикулярны и являются биссектрисами его угловСкачать

Параллелограмм. Свойства. Прямоугольник, ромб, квадрат. ЗАДАЧИСкачать