Приведите пример параллельных прямых из жизни

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые вокруг нас

Параллельные прямые вокруг нас.

МБОУ Фоминская ООШ

Класс: 7
Урок: геометрия
Учитель математики: Лимарева О.Ф.

Видео:Параллельные прямые. 6 класс.Скачать

Параллельные прямые в природе, конечно, есть,

Параллельные прямые в природе, конечно, есть, .

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Всех примеров их в быту нам не счесть

, Всех примеров их в быту нам не счесть.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Травинки и былинки растут перпендикулярно к земле,

Травинки и былинки растут перпендикулярно к земле, А значит они параллельны между собой все.

Видео:6 класс, 44 урок, Параллельные прямыеСкачать

Бабочки порхают на лугу, Параллельно друг другу и цветку

Бабочки порхают на лугу, Параллельно друг другу и цветку.

Видео:Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

Снег ,который кружит в вышине,

Снег ,который кружит в вышине, Параллельным слоем лежит на земле.

Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

Самолёт в вышине чертит параллели

Самолёт в вышине чертит параллели. А возвратившись с полёта, Садится параллельно на полосу взлёта.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Машины в пробке параллельно стоят

Машины в пробке параллельно стоят. А если водитель нарушит закон, то будет очень наказан он.

Видео:7 класс, 24 урок, Определение параллельных прямыхСкачать

В бассейне пловцы по параллельным дорожкам плывут,

В бассейне пловцы по параллельным дорожкам плывут, На стадионе легкоатлеты параллельно друг другу бегут. Дорожки никогда не пересекутся, Спортсмены никогда не столкнутся.

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Ток по параллельным прямым бежит,

Ток по параллельным прямым бежит, Поезд по рельсам мчит.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

На параллельные прямые в природе внимание обрати,

На параллельные прямые в природе внимание обрати, Ведь это и паутинки и цветы.

Видео:Параллельность прямых. 10 класс.Скачать

Из истории параллельности прямых

Из истории параллельности прямых

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Колонны Парфенона (Др.греция ,447—438 до н

«параллелой»- “рядом идущие” «друг подле друга проведенные» (перевод с греческого языка)

Колонны Парфенона (Др.греция ,447—438 до н. э) тоже параллельны.

Видео:Геометрия 7 Аксиома параллельных прямыхСкачать

Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той, ни с другой стороны между собой не…

разные определения параллельных прямых.

« Параллельные суть прямые,
которые, находясь в одной плоскости и
будучи продолжены в обе
стороны неограниченно,
ни с той, ни с другой
стороны между
собой не встречаются.»

Евклид
(в lll в. до н. э.)

Видео:Параллельные прямые циркулемСкачать

Две прямые, лежащие в одной плоскости и равностоящие друг от друга

разные определения параллельных прямых.

«Две прямые, лежащие
в одной плоскости
и равностоящие
друг от друга.»

Посидоний
( I в. до н.э. )

Видео:7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Современное определение Параллельные прямые -это прямые, лежащие в одной плоскости и не пересекающиеся

Параллельные прямые -это прямые, лежащие в одной плоскости и не пересекающиеся.

Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать

Проект по теме: Параллельные прямые в жизни

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

I . Теоретическая часть

1.1. Определение параллельных прямых . . 4

1.2. Параллельные прямые в жизни . 4

1.3. Иллюзии параллельных прямых . 5

1.4.Способы построения параллельных прямых . 6

1.5.Профессиональные способы построения параллельных прямых …………7

1.6.Применение параллельных прямых в геометрии …………………………..7

II . Практическая часть

2.1. Анкетирование учащихся. 9

2.2. Изготовление проектного продукта…………… . 9

Список литературы . 11

Каждый современный ученик должен быть всесторонне развитым, поэтому ему необходимо владеть не только математическими знаниями, но и знать историю математики . Школьная программа , к сожалению, не предусматривает изучение вопроса «История параллельных прямых», а способы построения параллельных прямых изучаются не в полном объёме. Исходя из этого, я решила расширить свои знания в области математики, а именно: изучить историю параллельных прямых, показать их значимость и закрепить умения строить параллельные прямые на линованной и нелинованной бумаге. Поэтому выбранная мной тема исследования актуальна.

Гипотеза: Без параллельных прямых невозможна наша жизнь.

Цель моего проекта: Показать необходимость и значимость параллельных прямых.

1. Собрать материал по теме, изучив литературу и Интернет-источники.

2. Изучить определения, способы построения и применение параллельных прямых в жизни .

3. Провести анкетирование обучающихся школы.

4. Составить буклет “ Параллельные прямые в жизни”.

1.1. Определение параллельных прямых

С греческого языка понятие «параллелос» переводится «рядом идущий» или «проведенный друг возле друга». Этот термин использовался в древней школе Пифагора еще до того, как параллельные прямые получили свое определение.

В домашних справочных и энциклопедических изданиях я нашла несколько определений понятиям «параллель» и «параллельные прямые». Например, в самом популярном толковом словаре русского языка С. И. Ожегова и Н. Ю. Шведовой параллелью в математике называется «Прямая, не пересекающаяся другой прямой, лежащей с ней в одной плоскости».

А из занимательного толкового словаря В. И. Даля – “ПАРАЛЛЕЛЬ” ж. — параллельная линия, равна во всех точках от другой отстоящая и потому никогда не могущая с нею встретиться.

В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются. В другом варианте определения, совпадающие прямые также считаются параллельными (Приложение 4, рис. 27)

Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида . Отказ от пятого постулата ведёт к геометрии Лобачевского (Приложение 8).

В геометрии Лобачевского вместо неё принимается следующая аксиома: Через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (Приложение 4, рис. 25; рис. 26).

Согласно историческим фактам Евклидом в III в. До н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых (Приложение 4, рис. 1).

В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в III в. Н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая l параллельна прямой m ранее обозначался «l=m». Позднее для обозначения параллельности прямых стали использовать привычный нам знак « ∥» , а знак равенства стали использовать для обозначения равенства чисел и выражений.

1.2. Параллельные прямые в жизни

Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий (Приложение 4, рис. 2). Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.) (Приложение 4, рис. 3). Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно (Приложение 4, рис. 4). Рельсы линий метро и железных дорог располагаются параллельно. Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий (Приложение 4, рис. 5; рис. 6 ; рис. 7).

На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться, рельсы также выполнены параллельными линиями. В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из-за иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

1.3.Иллюзии параллельных прямых

Слово «иллюзия» происходит от латинского illusere – обманывать.

Зрительная иллюзия – ошибка в зрительном восприятии, искажение пространственных соотношений признаков воспринимаемых объектов, ошибка в оценке и сравнении между собой длин отрезков, величин углов, расстояний между предметами, в восприятии формы предметов, совершаемые наблюдателем при определенных условиях.

Начало изучению зрительных иллюзий положило обнаружение немецким астрофизиком Ф. Цёлльнером (1860 г.) в рисунке купленной ткани эффекта визуального схождения и расхождения вертикальных параллельных линий при пересечении их короткими косыми линиями. Эта иллюзия наиболее сильно проявляется, когда пересекающееся линии образуют угол, равный 45° (Приложение 3, рис. 8).

На уроках геометрии, приступая к решению задачи, мы, как правило, первым делом строим чертёж, опираясь на свое зрительное восприятие. Но такой подход к решению задачи часто приводит к ошибочным выводам, а значит к неверному решению. Мы привыкли доверять собственному зрению, однако оно нередко обманывает нас, показывая то, чего в действительности не существует. В такие моменты мы сталкиваемся со зрительными иллюзиями — ошибками зрительного восприятия (Приложение 3, рис. 9; рис. 10; рис. 11).

В настоящее время люди не только поражаются обманам зрения и забавляются зрительными иллюзиями, но и сознательно используют их в своей практической деятельности. Иллюзии применяются в архитектуре, изобразительном, цирковом искусстве, кинематографии и даже в военном деле (Приложение 3, рис. 12; рис. 13; рис. 14).

Но с другой стороны мы столкнулись со странным явлением: устремляя взгляд далеко в бесконечность, можно увидеть пересечение параллельных прямых!

В чем же дело? Чтобы ответить на этот вопрос обратимся к великим ученым.

Но сначала я обратилась к учащимся 7 Б класса. С ними провела эксперимент «Иллюзии зрения». Учащимся задали вопрос: везде ли на картинках параллельные прямые? Результаты опроса таковы: участвовали 20 человек из них: 7 – 35% считают параллельно, 13 -65% нет (Приложение 3).

Вывод: в геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения.

Положительный момент: благодаря зрительным искажениям существует живопись.

1.4. Способы построения двух параллельных прямых

Изучив теоретические сведения, касающиеся параллельных прямых, возникла необходимость к изучению практических способов геометрических построений параллельных прямых на плоскости. Рассмотрим некоторые из них (Приложение 7):

Видео:7 класс, 27 урок, Об аксиомах геометрииСкачать

Приведите пример параллельных прямых из жизни

Две прямые на плоскости называются параллельными, если они не пересекаются.

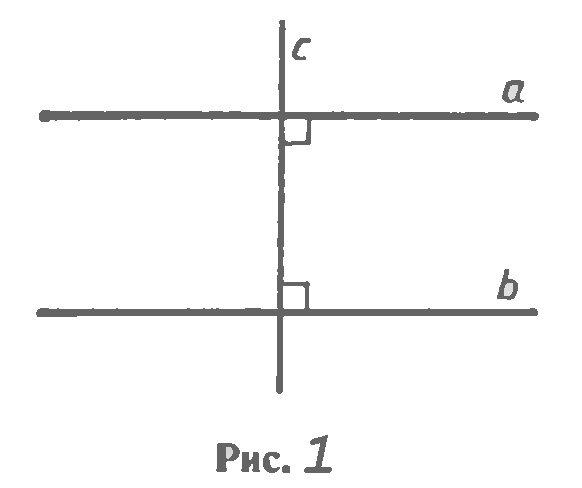
Параллельность прямых а и b обозначают так: а||b. На рисунке 1 изображены прямые a и b, перпендикулярные к прямой с. Такие прямые а и b не пересекаются, т. е. они параллельны.

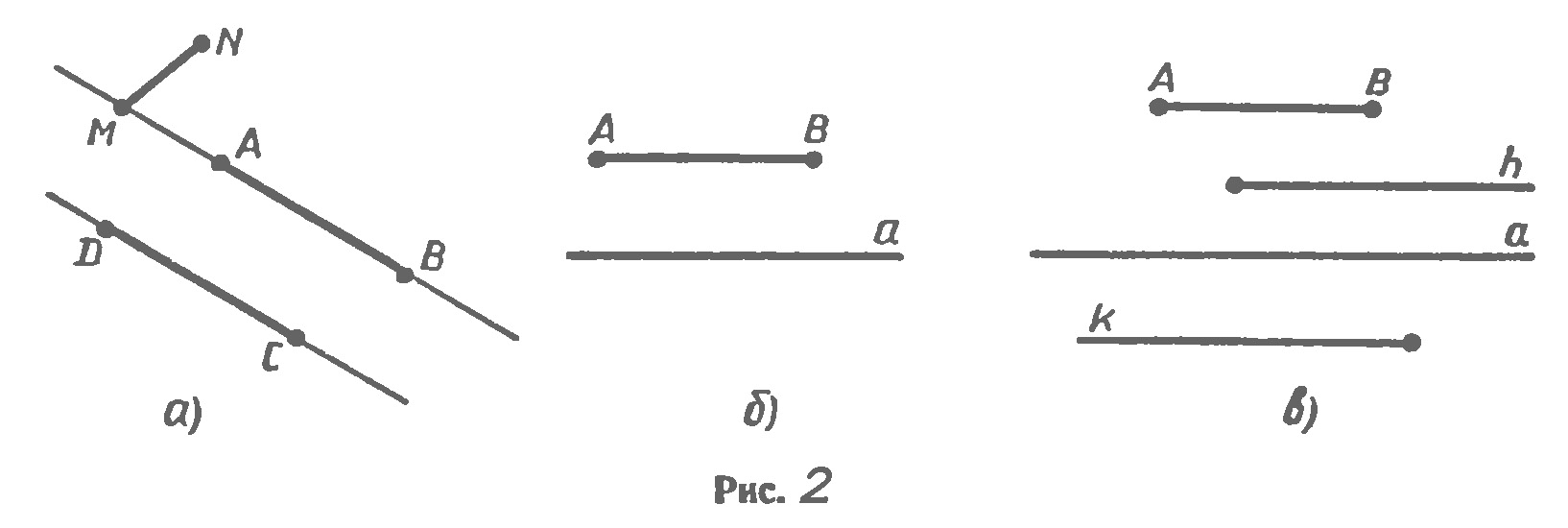
Наряду с параллельными прямыми часто рассматривают параллельные отрезки. Два отрезка называются параллельными, если они лежат на параллельных прямых. На рисунке (рис. 2,а) отрез­ки АВ и СD параллельны (АВ||СО) а отрезки МN и СD не параллельны. Аналогично определяется параллельность отрезка и прямой (рис. 2,б), луча и прямой, отрезка и луча, двух лучей(рис. 2,в).

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Признаки параллельности двух прямых

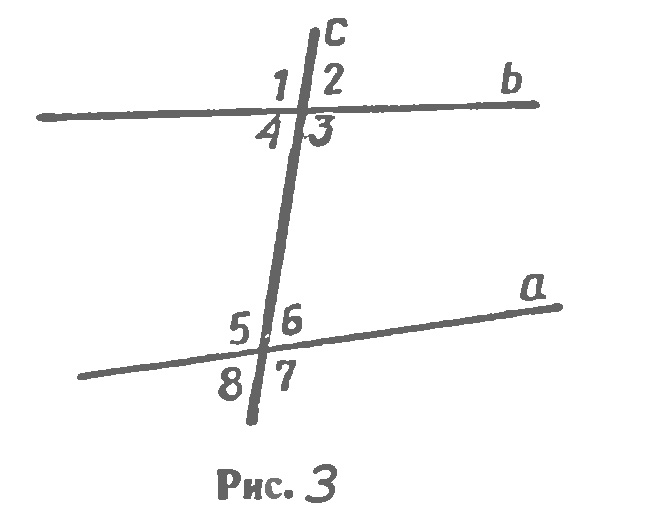
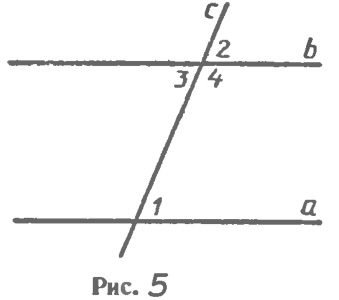
Прямая с называется секущей ми отношению к прямым а и b, если она пересекает их в двух точках (рис. 3). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 3 обозначены цифрами.

Некоторые пары этих углов имеют специальные названия:

накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Рассмотрим три признака параллельности двух прямых, связанные с этими парами углов.

Теорема.Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

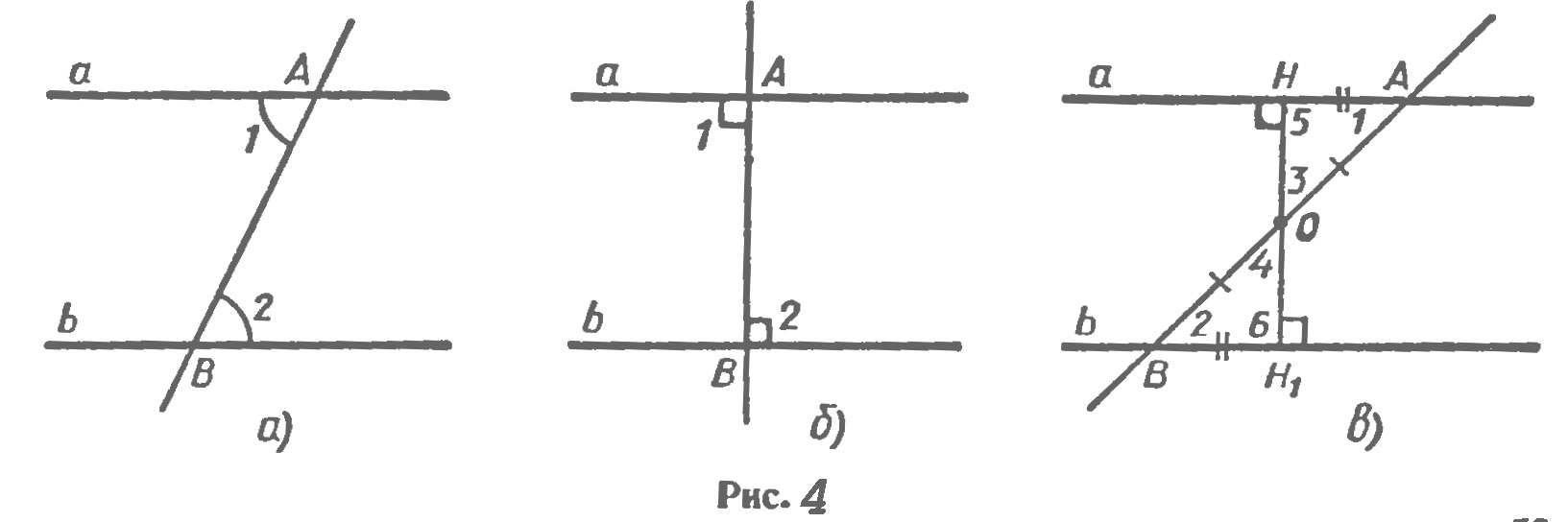
Доказательство.Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: ∠1=∠2 (рис. 4, а).

Покажем,что а||b. Если углы 1 и 2 прямые (рис. 4, б), то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны. Рассмотрим случай, когда углы 1 и 2 не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой а (рис. 4, в). На прямой b от точки В отложим отрезок ВН1 равный отрезку AH, как показано на рисунке 4, в, и проведем отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними (АО=ВО. АН=ВН1 ∠1=∠2), поэтому ∠3=∠4 и ∠15=∠16. Из равенства ∠3=∠4 следует, что точка Н1 лежит на продолжении луча ОН, т. е. точки Н, О и Н1 лежат на одной прямой, а из равенства ∠5=∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Значит, прямые а и b перпендикулярны к прямой НН1 поэтому они параллельны. Теорема доказана.

Теорема.Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство.Пусть при пересечении прямых а и b секущей с соответственные углы равны, например ∠1= ∠ 2 (рис. 5). Так как углы 2 и 3 — вертикальные, то ∠2=∠3. Из этих двух равенств следует, что ∠1=∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.

Теорема.Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Доказательство.Пусть при пересечении прямых а и b секущей с сумма односторонних углов равна 180°, например ∠1+∠4=180° (см. рис. 5). Так как углы 3 и 4 — смежные, то ∠3+∠4=180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны. Теорема доказана.

Практические способы построения параллельных прямых

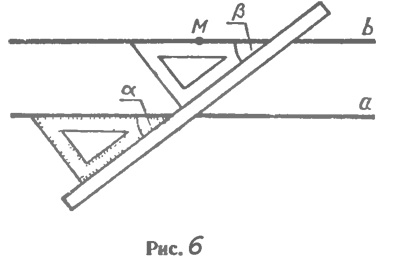
Признаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертежного угольника и линейки. Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертежный угольник к прямой а, а к нему линейку так, как показано на рисунке 103. Затем, передвигая угольник вдоль линейки, добьемся того, чтобы точ ка М оказалась на стороне угольника, и проведем прямую b. Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами альфа и бета, равны.

Еще есть способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертежной практике.

Аналогичный способ применяется при выполнении столярных работ, где для разметки параллельных прямых используется малка (две деревянные планки, скрепленные шарниром).

Интересный факт

Особое место в истории математики занимает пятый постулат Евклида (аксиома о параллельных прямых). Долгое время математики безуспешно пытались вывести пятый постулат из остальных постулатов Евклида и лишь в середине XIX века благодаря исследованиям Н. И. Лобачевского, Б. Римана и Я. Бойяи стало ясно, что пятый постулат не может быть выведен из остальных, а система аксиом, предложенная Евклидом, не единственно возможная.

Аксиома параллельных прямых

Еще древние греки придумали простой способ: как провести циркулем и линейкой через точку А, лежащую вне данной прямой l, другую прямую m, не пересекающую прямую l. Но единственно ли решение этой задачи? Или через точку А можно провести несколько разных прямых, не пересекающих исходную прямую m?

Евклид, видимо, первый среди эллинов понял, что ответ на этот вопрос нельзя получить, исходя из прочих свойств прямых и точек – тех, которые он сформулировал в виде аксиом и постулатов. Нужно ввести дополнительный постулат о единственности искомой прямой m – и назвать эту прямую параллельной!

А возможны ли иные формулировки постулата о параллельных прямых – не совместимые с постулатом Евклида? Например, можно предположить существование нескольких разных прямых, не пересекающих данную прямую l и проходящих через общую точку А. Приведет ли такое предположение к логическому противоречию или нет? Если нет, то возможны иные геометрии, кроме евклидовой!

Первую неевклидову геометрию изобрели в 1820-е годы сразу три талантливых математика: немец Карл Гаусс, русский Николай Лобачевский и венгр Янош Бойяи. Русский математик оказался самым смелым и упорным из троих открывателей. Он первый опубликовал свою книгу с предсказанием замечательных свойств неевклидовых фигур. Например, на плоскости Лобачевского сумма внутренних углов треугольника всегда меньше 180 градусов. Она принимает разные значения для разных треугольников; при этом два подобных треугольника обязательно равны!

В конце 19 века геометры Клейн и Пуанкаре изобрели довольно простые модели поверхностей, на которых воплощается геометрия Лобачевского. Еще раньше Риман заметил, что на обычной сфере воплощена третья возможная геометрия (проективная): в ней «параллельных» прямых вовсе нет, а сумма внутренних углов треугольника всегда больше, чем 180 градусов.

До начала 20 века считалось, что неевклидовы геометрии могут быть полезны только внутри математической науки. Но в 1910-е годы Эйнштейн создал Общую Теорию Относительности: она оказалась четырехмерным воплощением неевклидовой геометрии Лобачевского. С тех пор физики верят, что каждая непротиворечивая математическая конструкция воплощена где-нибудь в Природе. Возможно, что так оно и есть.

Историческая справка

В древние века, буквально 2500 лет назад, в известной школе Пифагора греческое слово «параллелос» начали употреблять, как геометрический термин, хотя определения параллельных прямых в те времена еще не знали. Но исторические факты говорят о том, что древнегреческий ученый Евклид в третьем веке до нашей эры, в своих книгах все же, раскрыл смысл такого понятия, как параллельные прямые.

Как вам уже известно, из пройденного материала в предыдущих классах, термин «параллелос» в переводе с греческого языка обозначает рядом идущий или проведенный друг возле друга.

В математике для обозначения параллельных прямых существует специальный знак. Правда, не всегда знак параллельности имел теперешний вид. Так, например, древнегреческий математик Папп в третьем веке нашей эры для обозначения параллельности пользовался знаком равно «=». И лишь в восемнадцатом веке, благодаря Уильяму Оутреду для обозначения параллельных прямых, стали использовать знак «//». Если есть, например, параллельные а и в, то на письме их следует записывать, как а//в

А вот знак «=» во всеобщее обращение ввел Рекорд и его стали использовать, как знак равенства.

Параллельные прямые в быту и повседневной жизни

С параллельными прямыми мы часто встречаемся в окружающей нас жизни, хотя, как правило, редко на этом акцентируем свое внимание. На уроках музыки, открывая нотную тетрадь, сразу же невооруженным взглядом мы видим линии нотного стана. Но параллельные линии вы можете увидеть не только в нотных тетрадях и сборниках песен, но и если внимательно присмотритесь к музыкальным инструментам. Ведь струны гитары, арфы или органа также расположены параллельно.

Подняв на улице глаза вверх, вы видите параллельно проходящие электрические провода. Оказавшись в метро или на железной дороге, также не сложно заметить, что рельсы расположены параллельно друг к другу.

Параллельные линии можно встретить повсюду. Они нам постоянно встречаются в быту, живописи. Без них не обойтись и в архитектуре, так как в строительстве зданий строго учитывается понятие параллельности.

Если вы внимательно посмотрите на изображение, то сразу же заметите в этих архитектурных сооружениях присутствие параллельных прямых. Возможно, они служат так долго и остаются красивыми благодаря тому, что архитекторы и инженеры при создании этих культовых зданий использовали параллельные прямые.

А задумывались ли вы когда-нибудь над тем, почему в линиях электропередач, провода располагаются параллельно? И представьте себе, чтобы было, если бы они не были бы параллельными и пересекались или соприкасались друг с другом. А это привело бы к нехорошим последствиям, при которых могло произойти замыкание, перебоям и отсутствию электричества. А что могло произойти с поездом, если бы рельсы не были бы параллельными? Об этом даже страшно подумать.

Вам всем хорошо известно, что параллельные прямые никогда не пересекаются. Но если вы долго будете смотреть вдаль, в бесконечность, то в итоге можете увидеть, как параллельные прямые пересекаются. В этом случае мы с вами столкнулись с иллюзией зрения. Может быть, только благодаря таким иллюзиям и зрительным искажениям и появилась живопись.

Домашнее задание

1. Назовите свои примеры, где вы в повседневной жизни, в быту или в природе сталкиваетесь с моментами или фактами параллельности.
2. Какие вы знаете способы, благодаря которым можно начертить параллельные прямые? Назовите эти способы.
3. Начертите параллельные прямые в тетради, способами, которые вам известны.
4. При каких условиях прямые, можно назвать параллельными?

1. Какие прямые называются параллельными?
2. Какие практические способы построения параллельных прямых существуют.?