Как определить какой четверти окружности принадлежит точка

((0;-) (frac) ()) — четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Как определить четверти на числовой окружности

Видео:Соответствие чисел точкам числовой окружностиСкачать

Четверть числовой окружности

Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac ) (;2π)) — четвертая четверть

Видео:КООРДИНАТНЫЕ ЧЕТВЕРТИ. В КАКОЙ КООРДИНАТНОЙ ЧЕТВЕРТИ НАХОДИТСЯ ТОЧКА? Примеры | МАТЕМАТИКА 6 классСкачать

Почему так важно определять какой четверти принадлежит угол?

Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .

Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.

Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.

Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла?
Основное тригонометрическое тождество. Запишем его.

Подставим известное, и проведем вычисления.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Про непостоянство четвертей:

Важно понимать, что, например, первой четверти принадлежат не только углы от (0) до (frac ) , но и углы от (2π) до (frac ) , и от (4π) до (frac ) , и от (6π) до (frac ) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.

((0;-) (frac ) ()) — четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Видео:Найти знак тригонометрической функции (bezbotvy)Скачать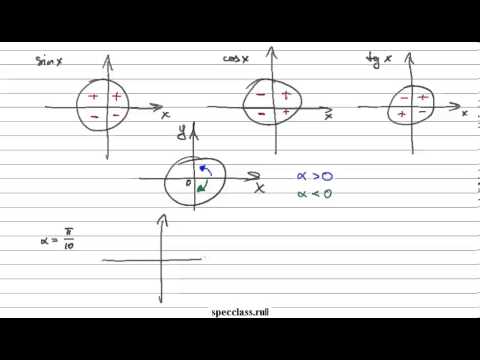

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac =frac =frac .) Тогда радианная мера угла: $$ angle AOB=frac =frac =frac $$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например:

Отметим на числовой окружности точки, соответствующие (frac , frac , frac , frac , pi), а также (-frac , -frac , -frac , -frac , -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac , frac , frac ), и (-frac ). Все четыре точки совпадают, т.к. begin Mleft(frac right)=Mleft(frac +2pi kright)\ frac -2pi=-frac \ frac +2pi=frac \ frac +4pi=frac end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac +2pi klt tltfrac +2pi k $$
Интервал
$$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac +2pi kleq tleqfrac +2pi k $$
Полуинтервал
$$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac +2pi kleq tltfrac +2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^ =frac .\ EC=60^ =frac .\ AE=EC+CD=90^ +30^ =120^ =frac .\ ED=EC+CD=60^ +90^ =150^ =frac . end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; frac ; frac ; frac ).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac =-90^ , frac =135^ \ frac =210^ , frac =315^ end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac ; 5pi; frac ; frac ).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac =frac cdotpi=-6pi+frac rightarrow frac =90^ \ 5pi=4pi+pirightarrow pi=180^ \ frac =frac pi=3pi-frac rightarrow pi-frac =frac \ frac =frac pi=7pi-frac rightarrow pi-frac =frac end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac =1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac approx frac =4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb )), запишите количество полученных базовых точек.

$$ frac $$	$$ -frac +2pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ frac +frac $$	$$ -frac $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

Видео:Определение значений по точкам на числовой окружностиСкачать

1. Конспект для учителя по теме «Числовая окружность»

Что такое числовая окружность? Для чего она нужна?

Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Сегодня мы будем учиться использовать единичную окружность.

Для успешной работы с единичной окружностью нужно знать всего три вещи.

Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику.

Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность.

Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов.

1. Какой угол называется углом поворота?

Угол поворота – это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.

1. Какой угол называется углом в 1?

Угол в 1— это центральный угол, опирающийся на дугу, длина которой равна части окружности.

1. Какой угол называется углом в 1 радиан?

Угол в 1 радиан — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.

1. Как выразить градусную меру угла в радианной?

1. Как определить какой четверти принадлежит угол?

В зависимости от того в какой координатной четверти окажется начальный радиус, угол α называют углом этой четверти:

0 Главная

Видео:Тригонометрическая окружность. Как выучить?Скачать

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac=frac=frac.) Тогда радианная мера угла: $$ angle AOB=frac<l_>=frac=frac $$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например:

Отметим на числовой окружности точки, соответствующие (frac, frac, frac, frac, pi), а также (-frac, -frac, -frac, -frac, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac, frac, frac), и (-frac). Все четыре точки совпадают, т.к. begin Mleft(fracright)=Mleft(frac+2pi kright)\ frac-2pi=-frac\ frac+2pi=frac\ frac+4pi=frac end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac+2pi klt tltfrac+2pi k $$
Интервал
$$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac+2pi kleq tleqfrac+2pi k $$
Полуинтервал
$$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac+2pi kleq tltfrac+2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^=frac.\ EC=60^=frac.\ AE=EC+CD=90^+30^=120^=frac.\ ED=EC+CD=60^+90^=150^=frac. end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; frac; frac; frac).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac=-90^, frac=135^\ frac=210^, frac=315^ end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; 5pi; frac; frac).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac=fraccdotpi=-6pi+fracrightarrow frac=90^\ 5pi=4pi+pirightarrow pi=180^\ frac=fracpi=3pi-fracrightarrow pi-frac=frac\ frac=fracpi=7pi-fracrightarrow pi-frac=frac end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ fracapprox frac=4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(fraclt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.

$$ frac $$	$$ -frac+2pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ frac+frac $$	$$ -frac $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

🎥 Видео

Числовая окружностьСкачать

9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Отбор корней по окружностиСкачать

Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Как найти координаты точек на тригонометрической окружностиСкачать

Точки на числовой окружностиСкачать

И в трещинах зеркальный круг. Часть 2. Агата Кристи. Мисс Марпл. Детектив. Аудиокнига.Скачать

Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать