Начертите треугольник авс вектор мм1 который не параллелен ни одной из сторон треугольника постройте

Подробное решение номер 1163 по геометрии для учащихся 7 класса, авторов Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин 2016

1163 С Начертите треугольник ABC, вектор ММ1, который не параллелен ни одной из сторон треугольника, и вектор а, параллельный стороне АС. Постройте треугольник А1В1С1, который получается из треугольника ABC параллельным переносом: а) на вектор ММ,; б) на вектор а.

Видео:№778. Начертите попарно неколлинеарные векторы а, b и c. Постройте векторы:Скачать

§ 2. Параллельный перенос и поворот

Параллельный перенос

Пусть — данный вектор. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что вектор равен вектору (рис. 329).

Параллельный перенос является движением, т. е. отображением плоскости на себя, сохраняющим расстояния. Докажем это. Пусть при параллельном переносе на вектор точки М и N отображаются в точки М₁ и N₁ (см. рис. 329). Так как , то . Отсюда следует, что ММ₁ || NN₁ и MM₁ = NN₁, поэтому четырёхугольник MM₁N₁N — параллелограмм. Следовательно, MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М₁ и N₁ (случаи, когда точки М и N расположены на прямой, параллельной вектору , рассмотрите самостоятельно). Таким образом, параллельный перенос сохраняет расстояния между точками и поэтому представляет собой движение. Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

Поворот

Отметим на плоскости точку О (центр поворота) и зададим угол а (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α (рис. 330). При этом точка О остаётся на месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении — по часовой стрелке или против часовой стрелки. На рисунке 330 изображён поворот против часовой стрелки.

Поворот является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.

Докажем это. Пусть О — центр поворота, α — угол поворота против часовой стрелки (случай поворота по часовой стрелке рассматривается аналогично). Допустим, что при этом повороте точки М и N отображаются в точки М₁ и N₁ (рис. 331). Треугольники OMN и ОМ₁N₁ равны по двум сторонам и углу между ними: ОМ = ОМ₁, ON = ON₁ и ∠MON = ∠M₁ON₁ (для случая, изображённого на рисунке 331, каждый из этих углов равен сумме угла α и угла M₁ON). Из равенства этих треугольников следует, что MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М, и N, (случай, когда точки О, М и N расположены на одной прямой, рассмотрите самостоятельно). Итак, поворот сохраняет расстояния между точками и поэтому представляет собой движение. Это движение можно представить себе как поворот всей плоскости вокруг данной точки О на данный угол α.

Задачи

1162. Начертите отрезок АВ и вектор . Постройте отрезок А1В1, который получается из отрезка АВ параллельным переносом на вектор .

1163. Начертите треугольник АВС, вектор , который не параллелен ни одной из сторон треугольника, и вектор , паралдельный стороне АС. Постройте треугольник А₁В₁С₁, который получается из треугольника АВС параллельным переносом: а) на вектор ; б) на вектор .

1164. Даны равнобедренный треугольник АВС с основанием АС и такая точка D на прямой АС, что точка С лежит на отрезке AD. а) Постройте отрезок BlD, который получается из отрезка ВС параллельным переносом на вектор . б) Докажите, что четырёхугольник ABB₁D — равнобедренная трапеция.

1165. Даны треугольник, трапеция и окружность. Постройте фигуры, которые получаются из этих фигур параллельным переносом на данный вектор .

1166. Постройте отрезок А₁В₁, который получается из данного отрезка АВ поворотом вокруг данного центра О: а) на 120° по часовой стрелке; б) на 75° против часовой стрелки; в) на 180°.

1167. Постройте треугольник, который получается из данного треугольника АВС поворотом вокруг точки А на угол 150° против часовой стрелки.

1168. Точка D является точкой пересечения биссектрис равностороннего треугольника АВС. Докажите, что при повороте вокруг точки D на угол 120° треугольник АВС отображается на себя.

1169. Докажите, что при повороте квадрата вокруг точки пересечения его диагоналей на угол 90° квадрат отображается на себя.

1170. Постройте окружность, которая получается из данной окружности с центром С поворотом вокруг точки О на угол 60° против часовой стрелки, если: а) точки О и С не совпадают; б) точки О и С совпадают.

1171. Постройте прямую а₁, которая получается из данной прямой а поворотом вокруг точки О на угол 60° по часовой стрелке, если прямая а: а) не проходит через точку О; б) проходит через точку О.

а) Построим окружность с центром О, которая касается прямой а (объясните, как это сделать). Пусть М — точка касания. При повороте вокруг точки О эта окружность отображается на себя, а касательная а отображается на некоторую касательную а₁ (объясните почему). Для построения прямой ах построим сначала точку М₁, в которую отображается точка М при повороте вокруг точки О на угол 60° по часовой стрелке, а затем проведём касательную а₁ к окружности в точке М₁.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Презентация по геометрии «Движение»(9 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

1 * ДВИЖЕНИЕ ОСЕВАЯ СИММЕТРИЯ ЦЕНТРАЛЬНАЯ СИММЕТРИЯ ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ПОВОРОТ Автор: Ладейнова О.С.

* 1 ОСЕВАЯ СИММЕТРИЯ Две точки М и М1 называются симметричными относительно прямой а ,если эта прямая проходит через середину отрезка М М1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе. Точка Р симметрична сама себе относительно прямой а. . а М М1 Р 0,1,2.

* 1 B1 A B k a) A k б) A B d 1.Для каждого из случаев, представленных на рисунке а, б, в, постройте А1 и В1, симметричные точкам А и В относительно данной прямой. 2.Существует ли на плоскости такая точка, для которой нет симметричной точки относительно данной прямой? 3. Докажите, что в каждом из рассмотренных случаев АВ = А1В1. А1 В1 В А1 В1 в)

* 1 ФИГУРЫ, ОБЛАДАЮЩИЕ ОСЕВОЙ СИММЕТРИЕЙ.

* 1 ЦЕНТРАЛЬНАЯ СИММЕТРИЯ О А В А1 В1 Две точки А иА1 называются симметричными относительно точки О, если О – середина отрезка АА1. Точка О считается симметричной самой себе. С D E D1 E1 C1 M Задача. Дан Δ СDE и точка М, лежащая вне Δ CDE. Постройте Δ C1D1E1, симметричный ΔCDE, относительно точки М.

* 1 Постройте точки А1 и В1, симметричные А и В относительно точки О, если : а) точка О лежит на отрезке АВ; а) А В О А1 В1 б) А В О В1 А1 б) точка О не лежит на прямой АВ.

* 1 Фигура называется симметричной относительно точки О если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. О Х

* 1 Отображение плоскости на себя. Представим себе, что каждой точке плоскости сопоставляется (ставится в соответствие ) какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя.

* 1 ПОНЯТИЕ ДВИЖЕНИЯ ДВИЖЕНИЕ- это отображение плоскости на себя, которое сохраняет расстояния между точками. Поясним это на примере осевой симметрии Дано: точки М и N,им симметричные относительно прямой а — М1, N1 Доказать : М N = M1 N1 Доказательство: 1) Построим NP  M M1, N1 P1 M M1 MNP = M1N1P1 (по двум катетам) объясните, почему это так. M N = M1 N1 а М М1 N N1 P1 P 0,1,2.

* 1 Пусть р –данный вектор. Параллельным переносом на вектор р называется отображение плоскости на себя, при котором каждая точка А отображается в такую точку А1, что вектор АА1 равен вектору р. Параллельный перенос является движением. Доказательство: так как АА1= р, ВВ1= р, то АА1=ВВ1. 1)АА1=ВВ1, 2)АА1 ║ ВВ1. АВВ1А1 –параллелограмм. АВ=А1В1. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС р А В В1 А1 0,5

* 1 2. ЕЕ1 = РР1 1. СС1 = РР1. С Е Р Р1 С1 Е1 Задача 1. Начертите отрезок СЕ и вектор РР1. Постройте отрезок С1Е1, который получится из отрезка СЕ параллельным переносом на вектор РР1. Построение. 3. Отрезок С1Е1.

* 1 Задача 2. Начертите Δ АВС, вектор ММ1, который не параллельный ни одной из сторон треугольника, и вектор а, параллельный стороне АС. Постройте Δ А1В1С1, который получится из Δ АВС параллельным переносом: а) на вектор ММ1; б) на вектор а. а) б) М М1 В С С1 В1 А1 А а А В С В1 А1 С1

* 1 М ПОВОРОТ О М1 a Отметим на плоскости точку О (центр поворота) и зададим угол a ( угол поворота). Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что ОМ=ОМ1 и угол МОМ1 равен a. При этом точка О остаётся на месте, т.е. отображается сама на себя, а все остальные поворачиваются вокруг точки О в одном и том же направлении – по часовой стрелке или против часовой стрелки. 0,1,2,5.

* 1 О 3.ON1 = ON. N N1 P1 P Поворот является движением, то есть отображением плоскости на себя, при котором сохраняются расстояния. Задача 3. Постройте отрезок N1P1, который получается из данного отрезка NP поворотом вокруг данного центра О: а) на угол 135 по часовой стрелке; б) на 70 против часовой стрелки. Построение. 1. Луч ON. 2.  NON1 = 135º 4. Луч ОР. 5.  POP1= 135° 6. ОР = ОР1. 7. Отрезок N1P1.

* 1 поворот Задача 4. Постройте треугольник, который получается из данного треугольника АВС поворотом вокруг точки М на угол 90° против часовой стрелки. А В С В1 А1 С1 М

* 1 А В С В1 С1 160° № 1167. Постройте треугольник, который получается из данного треугольника АВС поворотом вокруг точки А на угол 160° против часовой стрелки. Д/З п. 116, № 1162, 1166, 1164 (а).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Задание № 1163 — Геометрия 9 класс (Атанасян)Скачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 512 475 материалов в базе

Другие материалы

• 29.08.2016
• 2705
• 19

• 29.08.2016
• 439
• 1

• 29.08.2016
• 1873
• 8

• 29.08.2016
• 535
• 0

• 29.08.2016
• 412
• 0

• 29.08.2016
• 437
• 0

• 29.08.2016
• 347
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 29.08.2016 1808
• PPTX 1.8 мбайт
• 11 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Ладейнова Ольга Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет
• Подписчики: 0
• Всего просмотров: 14102
• Всего материалов: 13

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Большинство российских вузов используют смешанный формат обучения

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

В школьном курсе мировой истории планируют уделить больше внимания Азии и Африке

Время чтения: 1 минута

Все школы Оренбурга переводят на дистанционное обучение с 28 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📽️ Видео

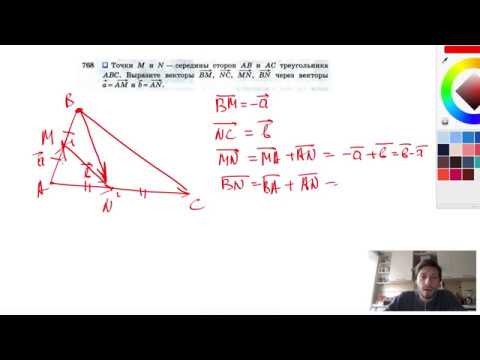
№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать

№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

№767. Дан треугольник ABC. Выразите через векторы а=АВ и b=АС следующие векторы:Скачать

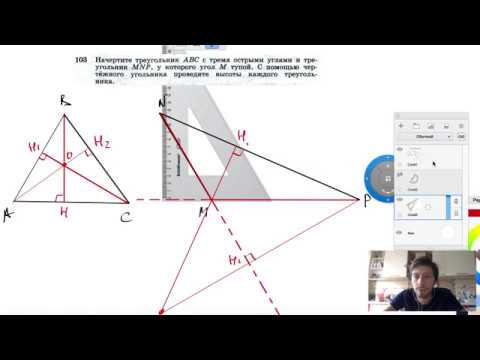
№103. Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой.Скачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

9 класс. Контрольная №1 (из 6). Тема: Векторы. Подробное решение с объяснением. Пробуем свои силы!Скачать

Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

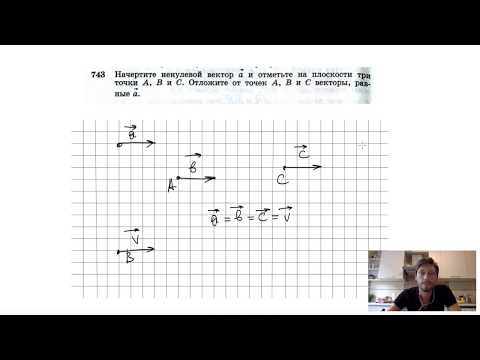
№743. Начертите ненулевой вектор a и отметьте на плоскости три точки A, B, C.Скачать