В любом вписанном четырехугольнике сумма противоположных углов равна 180

Четырехугольники, вписанные в окружность. Теорема Птолемея

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

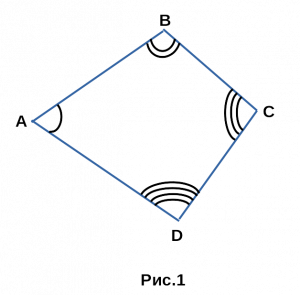
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

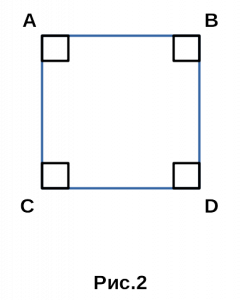
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

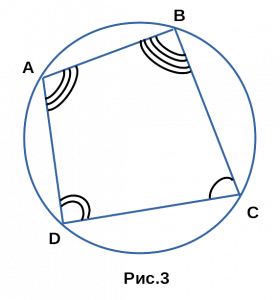
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

В любом вписанном четырехугольнике сумма противоположных углов равна 180

ВПИСАННЫЕ И ОПИСАННЫЕ МНОГОУГОЛЬНИКИ,

§ 106. СВОЙСТВА ВПИСАННЫХ И ОПИСАННЫХ ЧЕТЫРЁХУГОЛЬНИКОВ.

Теорема 1. Сумма противоположных углов вписанного четырёхугольника равна 180°.

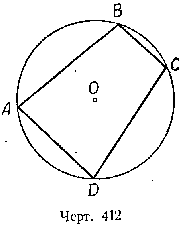
Пусть в окружность с центром О вписан четырёхугольник ABCD (черт. 412). Требуется доказать, что / А + / С = 180° и / В + / D = 180°.

/ А, как вписанный в окружность О, измеряется 1 /₂ BCD.
/ С, как вписанный в ту же окружность, измеряется 1 /₂ BAD.

Следовательно, сумма углов А и С измеряется полусуммой дуг BCD и BAD в сумме же эти дуги составляют окружность, т. е. имеют 360°.
Отсюда / А + / С = 360° : 2 = 180°.

Аналогично доказывается, что и / В + / D = 180°. Однако это можно вывести и иным путём. Мы знаем, что сумма внутренних углов выпуклого четырёхугольника равна 360°. Сумма углов А и С равна 180°, значит, на сумму других двух углов четырёхугольника остаётся тоже 180° .

Теорема 2 (обратная). Если в четырёхугольнике сумма двух противоположных углов равна 180°, то около такого четырёхугольника можно описать окружность.

Пусть сумма противоположных углов четырёхугольника ABCD равна 180°, а именно
/ А + / С = 180° и / В + / D = 180° (черт. 412).

Докажем, что около такого четырёхугольника можно описать окружность.

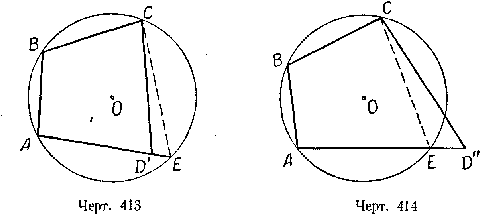
Доказательство. Через любые 3 вершины этого четырёхугольника можно провести окружность, например через точки А, В и С. Где будет находиться точка D?

Точка D может занять только одно из следующих трёх положений: оказаться внутри круга, оказаться вне круга, оказаться на окружности круга.

Допустим, что вершина окажется внутри круга и займёт положение D’ (черт. 413). Тогда в четырёхугольнике ABCD’ будем иметь:

Продолжив сторону AD’ до пересечения с окружностью в точке Е и соединив точки Е и С, получим вписанный четырёхугольник АВСЕ, в котором по прямой теореме

Из этих двух равенств следует:

но этого быть не может, так как / D’, как внешний относительно треугольника CD’E, должен быть больше угла Е. Поэтому точка D не может оказаться внутри круга.

Так же доказывается, что вершина D не может занять положение D» вне круга (черт. 414).

Остаётся признать, что вершина D должна лежать на окружности круга, т. е. совпасть с точкой Е, значит, около четырёхугольника ABCD можно описать окружность.

Следствия. 1. Вокруг всякого прямоугольника можно описать окружность.

2. Вокруг равнобедренной трапеции можно описать окружность.

В обоих случаях сумма противоположных углов равна 180°.

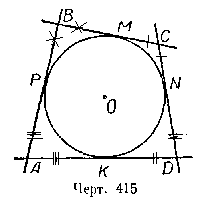
Теорема 3. В описанном четырёхугольнике суммы противоположных сторон равны. Пусть четырёхугольник ABCD описан около окружности (черт. 415), т. е. стороны его АВ, ВС, CD и DA — касательные к этой окружности.

Требуется доказать, что АВ + CD =AD + ВС. Обозначим точки касания буквами М, N, К, Р, На основании свойств касательных, проведённых к окружности из одной точки (§ 75), имеем:

АР = АК;
ВР = ВМ;
DN = DK;
CN = СМ.

Сложим почленно эти равенства. Получим:

АР + ВР + DN + CN = АК + ВМ +DK + СМ,

т. е. АВ + CD = AD + ВС, что и требовалось доказать.

1. Во вписанном четырёхугольнике два противоположных угла относятся как 3 : 5,
а другие два относятся как 4 : 5. Определить величину этих углов.

2. В описанном четырёхугольнике сумма двух противоположных сторон равна 45 см. Остальные две стороны относятся как 0,2 : 0,3. Найти длину этих сторон.

Сумма углов четырехугольника

Свойства

1. Сумма углов четырехугольника равна 360°.
   ∠A + ∠B + ∠C + ∠D = 360°.
   
2. Если четырехугольник правильный, то каждый угол по 90°
   и этот четырехугольник является квадратом.
   ∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
   ABCD — квадрат.
   
3. Сумма противоположных углов четырехугольника равна 180°,
   если около четырехугольника описана окружность.
   ∠A + ∠С = ∠В + ∠D = 180°.
   

Такие четырехугольники называют вписанными.

Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.

📽️ Видео