На плоскости дано 100 окружностей составляющих связную фигуру (3 видео)

Теория графов

Пятков Александр Дмитриевич , Учитель информатики
Москва

Посвятить учеников в теорию графов

Посмотреть публикацию
Скачать свидетельство о публикации(справка о публикации находится на 2 листе в файле со свидетельством)

Подборка задач и теории для 6-7 класса.

Автор: Пятков Александр Дмитриевич

Данный материал раскрывает основные определения и теоремы темы «графы». Данная тема помогает решать множество олимпиадных задач по математике, а также помогает понять часть принципов используемых в программировании.

Граф — совокупность точек, некоторые из которых соединены отрезками. Точки называются вершинами графа, отрезки ребрами.

1.В деревне 9 домов. Известно, что у Гоши соседи Иван и Роман, Максим сосед Ивану и Михаилу, Виктор — Алексею и Андрею, а также по соседству живут Константин с Андреем, Иван с Михаилом, Константин с Алексеем, Михаил с Романом и больше соседей в означенной деревне нет (соседними считаются дворы, у которых есть общий участок забора). Может ли Гоша огородами пробраться к Андрею за яблоками?

2.В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли добраться из города 1 в город 9?

3.В некотором государстве 6 городов и 10 автодорог, каждая из которых связывает какие-то два города. Между городами устанавливается авиационное сообщение, исходя из принципа экономии: авиационная линия между двумя городами устанавливается тогда и только тогда, когда автомобильная дорога между этими городами отсутствует. Сколько авиалиний будет проведено?

Степень вершины — количество ребер, выходящих из данной вершины.

4.В стране 1329 городов, из каждого выходит по 4 дороги. Сколько всего дорог в стране?

5.Докажите, что не существует графа с пятью вершинами, степени которых равны 4, 4, 4, 4, 2.

6.Вася считает, что в его классе у всех разное число друзей-одноклассников. Не ошибается ли он?

7.Иван утверждает, что среди любых а) четырёх; б) пяти; в) шести человек обязательно найдётся либо трое знакомых друг с другом, либо трое незнакомых. Не завирается ли он?

8.Петя заметил, что у всех его 25 одноклассников различное число друзей в этом классе. Сколько друзей у Пети? (Укажите все решения.)

9.Докажите, что существует граф с 2n вершинами, степени которых равны 1, 1, 2, 2, . n, n.

10.Докажите, что не существует многогранника, у которого было бы ровно семь ребер.

11.Верно ли, что два графа изоморфны, если

а)у них по 10 вершин, степень каждой из которых равна 9?

б)у них по 8 вершин, степень каждой из которых равна 3?

в)они связны, без циклов и содержат по 6 ребер?

12.В некотором городе на любом перекрестке сходятся ровно 3 улицы. Улицы раскрашены в три цвета так, что на каждом перекрестке сходятся улицы трех разных цветов. Из города выходят три дороги. Докажите, что они имеют разные цвета.

1.Волшебная страна Фарг почти вся состоит из непреодолимых гор и рек. В ней есть шесть городов: А, Б, В, Г, Д и Е. Известно, что из А проложены дороги в Б и Г, из Б — в А, Г и Д, из В — в Г и Е, из Г — в В и Д, из Д — в Б и Г, из Е — только в В. Все остальные дороги непроходимы.

а)Нарисуйте карту страны Фарг.

б)Нарисуйте карту так, чтобы дороги не пересекались.

в)Может ли житель города А попасть в город Д, если ему нельзя проходить через Г?

г)Сможет ли он при тех же условиях попасть в город Е?

Будем называть графом набор точек (вершин), некоторые из которых соединены между собой линиями (рёбрами). Граф называется связным, если от любой его вершины можно по рёбрам добраться до любой другой (и несвязным иначе). Степенью вершины называется число выходящих из нее ребер. Два графа будем называть одинаковыми, если выполнены следующие два условия:

1)у них равное число вершин;

2)вершины каждого графа можно пронумеровать так, что если вершины с номерами i и j соединены ребрами в одном графе, то вершины с теми же номерами соединены таким же числом рёбер и в другом графе, а если вершины с номерами i и j не соединены ребром в одном графе, то вершины с теми же номерами не соединены и в другом графе.

2.Найдите все наборы одинаковых графов:

а)графов с двумя вершинами; б)графов с тремя рёбрами;

в)связных графов с тремя рёбрами; г)несвязных графов с четырьмя вершинами.

4.Можно ли начертить данные графы одним росчерком (не отрывая руки от бумаги и не проходя по ребру дважды)?

5.Докажите, что граф с более чем двумя вершинами нечётной степени невозможно начертить одним росчерком (не отрывая ручки от бумаги и не проводя никакое ребро дважды).

6.Дана проволока длиной 12 см. Можно ли сложить из нее каркас куба с ребром в 1 см? Проволоку нельзя резать.

7.Докажите, что среди любых шести человек обязательно найдутся либо три попарно знакомых, либо три попарно незнакомых.

8.Пешеход обошел шесть улиц одного города, пройдя каждую ровно два раза, но не смог обойти их, пройдя каждую лишь один раз. Могло ли такое быть, если в городе нет тупиков?

Определение : Граф называется двудольным, если его вершины можно раскрасить в два цвета так, чтобы рёбра соединяли только пары вершин разного цвета.

Теорема о числе рёбер двудольного графа.

а) Если в двудольном графе п белых вершин, и все они имеют степень s, то всего в графе ns рёбер.

б) Число рёбер равно сумме степеней всех белых вершин (а также равно сумме степеней всех чёрных вершин).

Лемма о рукопожатиях

Сумма степеней всех вершин графа равна удвоенному количеству рёбер.

Задача 1. Нарисуйте двудольный граф, где чёрные и белые вершины — это соответственно чёрные и белые клетки доски 3 х 3, а рёбра соответствуют ходам коня.

Задача 2. Каждый граф можно превратить в двудольный, покрасив все его вершины в белый цвет и добавив чёрную вершину в середину каждого ребра. Сколько вершин каждого цвета и сколько рёбер у полученного графа, если у исходного было v вершин и г рёбер?

Задача 3. В классе 20 человек. На праздник каждый мальчик подарил каждой девочке по цветку.

а) Какое наибольшее число цветков могло быть подарено?

б) Тот же вопрос, если в классе 21 человек.

в) Сформулируйте теорему о максимальном количестве рёбер в двудольном графе с 2п вершинами; с 2п + 1 вершинами.

Задача 4. Можно ли нарисовать на плоскости 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?

Задача 5. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 — по 4 друга, а 10 — по 5 друзей?

Задача 6. Джон, приехав из Диснейленда, рассказывал, что там, на заколдованном озере имеются 7 островов, с каждого из которых ведет 1, 3 или 5 мостов. Верно ли, что хотя бы один из этих мостов обязательно выходит на берег озера?

Задача 7. Докажите, что связный граф, в котором степень каждой вершины чётна, при удалении любого ребра остаётся связным.

Задача 8. В шахматном турнире в один круг участвуют 17 человек. Верно ли, что в любой момент турнира найдется шахматист, сыгравший к этому моменту четное число партий(может быть, ни одной)?

Задача 9. Футбольный мяч сшит из 32 лоскутов: белых шестиугольников и черных пятиугольников. Каждый черный лоскут граничит только с белыми, а каждый белый – с тремя черными и тремя белыми. Сколько лоскутов белого цвета?

Определение: Связный граф без циклов называется деревом.

Теорема 1. В любом дереве (в котором более одной вершины) есть вершина, из которой выходит ровно одно ребро.

Теорема 2. В дереве количество вершин на 1 больше количества рёбер:

Теорема 3. Из любого связного графа можно удалить часть рёбер (не удаляя вершин) так, чтобы осталось дерево.

Его называют остовным деревом графа или каркасом графа.

Задача 0. Выделите остовное дерево в полном графе из 4, 5, 6 вершин.

Задача 1. Нарисуйте все деревья с пятью вершинами. Объясните, почему других деревьев нет.

Задача 2. В графе все вершины имеют степень три. Докажите, что в нём есть цикл.

Задача 3. Докажите, что в дереве (в котором больше одной вершины) найдутся хотя бы две висячие вершины.

Задача 4. Волейбольная сетка имеет вид прямоугольника размером 50 х 600 клеток. Какое наибольшее число раз можно разрезать составляющие сетку верёвочки так, чтобы сетка не распалась на куски?

Задача 5. Докажите, что при удалении любого ребра из дерева оно превращается в несвязный граф.

Задача 6. Докажите, что связный граф, в котором вершин на одну больше, чем ребер, является деревом (то есть не содержит циклов).

Задача 1. В некотором государстве 99 городов, некоторые пары городов соединены дорогами длиной в 1, 3 или 5 вёрст, причём от каждого города до каждого по этим дорогам можно добраться ровно одним способом. Из каждого города в каждый другой отправились гонцы с важным донесением. Докажите, что суммарное расстояние, пройденное гонцами, делится на 4.

Задача 2. На Малом Мехмате дети договорились послать друг другу электронные письма. Те из них, у кого число знакомых чётно, отправят письма всем знакомым, а те, у кого число знакомых нечётно, отправят письма всем незнакомым. Придя домой и включив компьютер, Гоша увидел, что ему пришло 99 писем. Докажите, что он получит ещё хотя бы одно.

Задача 3. Докажите, что среди любых шести человек всегда найдутся либо трое попарно знакомых, либо трое попарно незнакомых.

Задача 4. На встречу выпускников пришло 45 человек. Оказалось, что любые двое из них, имеющие одинаковое число знакомых среди пришедших, не знакомы друг с другом. Какое наибольшее число пар знакомых могло быть среди участвовавших во встрече?

Задача 5. Можно ли раскрасить ребра куба в красный и чёрный цвета так, чтобы муравей мог пройти из любой вершины в любую, гуляя только по красным ребрам, а жук — только по чёрным?

Задача 6. Из спичек выложили клетчатый квадрат 8 х 8 со стороной клетки в одну спичку. Какое наименьшее число спичек надо убрать, чтобы с любой клетки на любую другую можно было пройти, не перепрыгивая через спички?

Задача 7. На плоскости дано 100 окружностей, составляющих связную фигуру. Доказать, что эту фигуру можно нарисовать, не отрывая карандаша от бумаги, и не проводя дважды одну и ту же линию.

Задача 8. В стране Древляндия 101 город, некоторые из них соединены дорогами. При этом любые два города соединяет ровно один маршрут. Сколько в этой стране дорог?

Содержание

Задачи и упражнения
На плоскости дано 100 окружностей
«ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ Методические указания Рязань 2010 УДК 519.17 Элементы теории графов: методические указания / Рязан. гос. радиотехн. ун-т; сост.: А.И. Сюсюкалов, Е.А. . »
На плоскости дано 100 окружностей
Задачи на тему «Геометрия». Программирование на Си, С++ (консольные приложения).
Окружность через три точки
Прямая пересекающая окружности
Параллельность прямых
Точки на сторонах треугольников
Площадь выпуклого многоугольника
📸 Видео

Видео:Окружность. 7 класс.Скачать

Задачи и упражнения

Рис. 50 Рис. 51

7. Перечислите все полные графы, являющиеся уникурсальными.

Можно ли эту решетку составить

а) из 5 ломаных длины 8;
б) из 8 ломаных длины 5? Рис. 57
10. Докажите, что любой разрез графа, являющегося эйлеровым циклом, содержит по крайней мере два ребра и что он обязательно состоит из четного числа ребер.

Видео:Уравнение окружности (1)Скачать

На плоскости дано 100 окружностей

Видео:1 2 4 сопряжение окружностейСкачать

«ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ Методические указания Рязань 2010 УДК 519.17 Элементы теории графов: методические указания / Рязан. гос. радиотехн. ун-т; сост.: А.И. Сюсюкалов, Е.А. . »

7. Докажите, что граф с n вершинами, степень каждой из которых не менее 8. На конференции присутствует 50 учёных, каждый из которых знаком по крайней мере с 25 участниками конференции.

Докажите, что найдутся четверо из них, которых можно усадить за круглый стол так, чтобы каждый сидел рядом со знакомыми ему людьми.

9. В некоторой группе людей у каждого есть один враг и один друг. [Если A – друг (враг) B, то B – друг (враг) A ]. Докажите, что этих людей можно разбить на две компании так, что в каждой компании не будет ни врагов, ни друзей.

10. В теннисном турнире каждый игрок команды «синих»

встречается с каждым игроком команды «красных». Число игроков в командах одинаково и не больше восьми. «Синие» выиграли в четыре раза больше встреч, чем «красные». Сколько человек в каждой из команд?

11. В двух делегациях вместе 22 человека. При встрече члены одной делегации обменялись рукопожатиями с членами другой делегации. Всего было сделано 121 рукопожатие. Докажите, что в делегациях одинаковое число членов.

12. Каждый из учеников 9 «а» класса дружит ровно с тремя учениками 9 «б» класса, а каждый ученик 9 «б» класса дружит ровно с тремя учениками 9 «а» класса. Докажите, что число учеников в этих классах одинаково.

13. Можно ли так нарисовать 5 горизонтальных и 4 вертикальных отрезка, чтобы каждый горизонтальный отрезок пересекался ровно с тремя вертикальными, а каждый вертикальный ровно с тремя горизонтальными?

Определение. Если граф имеет цикл, содержащий все рёбра, то он называется эйлеровым графом, а цикл называется эйлеровым циклом.

Теорема 2.1. Для того чтобы граф G был эйлеровым, необходимо и достаточно, чтобы он был: 1) связен; 2) все его степени вершин были чётными.

Д о к а з а т е л ь с т в о. Необходимость. Связность следует из определения эйлерова цикла, поэтому условие 1 необходимо.

Когда эйлеров цикл проходит через вершину, он должен войти в неё по одному ребру и выйти по другому, поэтому условие также необходимо.

Достаточность. Пусть условия 1 и 2 выполнены. Начнём цепь P в вершине v0 и будем продолжать её через разные рёбра, пока этот процесс не закончится в v0, в силу конечности графа G и того, что v0 и другие вершины имеют чётную степень. Если P содержит не все рёбра G, то удалим из G цепь P, состоящую из рёбер этого цикла.

Графы G и P имеют вершины с чётными степенями, поэтому оставшийся граф P (после удаления из G цепи P ) также имеет чётные вершины.

Так как G связен, то в P найдётся вершина v*, инцидентная рёбрам из P. Из v* можно построить новую цепь P из рёбер P. Такая цепь может закончиться только в v*. Из P и P составим новый цикл P P v0, v* P P v*, v0 (рис. 6).

Если цикл P не является эйлеровым, то это построение повторяется. В силу конечности графа этот процесс завершится построением эйлерова цикла. Теорема доказана.

Теорема 2.2. Для того чтобы в связном графе G имелась цепь P v0, v*, содержащая все его рёбра по одному разу, необходимо и достаточно, чтобы v0, v* были единственными вершинами нечётной степени.

Для доказательства достаточно добавить к графу G новое ребро v0, v*, и все его вершины станут чётными. Новый граф обладает эйлеv, v P v0, v* (рис. 7).

Следствие. Если в графе больше двух нечётных вершин, то его правильный обход (без повторения рёбер) невозможен.

Теорема 2.3. В связном графе с 2k нечётными вершинами имеется семейство из k цепей, которые в совокупности содержат все рёбра графа по одному разу.

vk, v2 k, тогда в новом графе найдётся эйлеров цикл P. При удалении рёбер vi, vk i i 1, k граф распадётся на k цепей, содержащих все рёбра.

Теорема 2.4. Связный граф является эйлеровым тогда и только тогда, когда его рёбра можно разбить на непересекающиеся простые циклы.

Д о к а з а т е л ь с т в о. Необходимость. Пусть G – эйлеров граф. Начнём проходить эйлеров цикл графа, начиная с любой вершины v1, до тех пор, пока не попа- дём в вершину w, в которой уже были (см. рис. 8).

Часть эйлерова цикла от вершины w до вершины w образует простой цикл С1.

Удалим из графа G рёбра цикла С1. В полученном графе G2 все вершины имеют чётную степень, следовательно, все его компоненты будут эйлеровыми графами. Так же как и ранее, выделим в G2 цикл С2. Указанный процесс будем продолжать, пока не разобьём все рёбра графа на простые циклы.

Достаточность. Пусть рёбра графа разбиты на простые циклы. Объединим их в эйлеров цикл, как это делали при доказательстве достаточности в теореме 2.1. Теорема доказана.

1. Схема мостов города Кёнигсберга изображена на рис. 9. Можно ли совершить прогулку, пройдя по каждому мосту ровно один раз?

2. Можно ли нарисовать граф, изображённый а) на рисунке 10, а; б) на рисунке 10, б, не отрывая карандаша от бумаги и проводя каждое ребро ровно один раз?

3. Можно ли прогуляться по парку и его окрестностям (рис. 11) так, чтобы при этом перелезть через каждый забор ровно один раз?

4. а) Дан кусок проволоки длиной 120 см.

Можно ли, не ломая проволоки, изготовить каркас куба с ребром 10 см? б) Какое наименьшее число раз придётся ломать проволоку, чтобы всё же изготовить требуемый каркас?

5. Докажите, что связный граф с 2n нечётными вершинами можно нарисовать, оторвав карандаш от бумаги ровно n 1 раз и не проводя никакое ребро дважды.

6. Можно ли, не отрывая карандаша от бумаги и не проводя по одной линии дважды, нарисовать: а) квадрат с диагоналями;

б) правильный пятиугольник с диагоналями?

7. Турист обошёл 6 улиц одного города, пройдя каждую ровно два раза, но не смог обойти их, пройдя каждую по одному разу. Могло ли так быть, если а) улицы могут оканчиваться тупиком; б) конец каждой улицы – перекрёсток?

8. На плоскости дано 100 окружностей, составляющих связную (не распадающуюся на части) фигуру. Доказать, что эту фигуру можно нарисовать, не отрывая карандаша от бумаги и не проводя дважды одну и ту же линию.

Определение 3.1. Деревом называется связный граф без циклов.

Таким образом, в дереве невозможно, передвигаясь по различным рёбрам, вернуться в исходную вершину.

Определение 3.2. Висячей вершиной называется вершина, из которой выходит ровно одно ребро.

Наглядное представление для дерева можно получить с помощью следующей конструкции (см. рис. 12). Из вершины v проведём рёбра в соседние вершины v1, v2, v3, из них проведём рёбра к их «соседям» v4, v5, v6, v7, v8, v9, v10 и т.д. Исходная вершина v0 называется корнем. Отметим, что каждая вершина может быть корнем.

Теорема 3.1. Граф, в котором любые две вершины соединены ровно одной цепью, является деревом.

цикл, тогда любые две вершины цикла соединены по крайней мере двумя путями. Противоречие.

Теорема 3.2. В дереве любые две вершины соединены ровно одной цепью.

Д о к а з а т е л ь с т в о. Пусть найдутся две вершины, соединённые двумя разными путями; а) если эти пути не имеют общих рёбер, то из них получим цикл; б) если пути имеют общие рёбра, то выберем первую вершину v0, в которой пути расходятся. За вершиной v0 на первом пути выберем вершину v1, принадлежащую второму пути, тогда участки первого и второго путей между v0 и v1 образуют цикл. Противоречие.

Таким образом, можно дать другое определение дерева.

Определение 3.3. Дерево – граф, в котором любые две вершины соединены ровно одной цепью.

Лемма. В любом дереве есть висячая вершина.

Д о к а з а т е л ь с т в о. Рассмотрим произвольную вершину v0 и пойдём по любому ребру из неё в другую вершину v1.

Если выходящих рёбер из новой вершины v1 нет, то остаёмся в ней, а в противном случае идём по любому другому ребру дальше. Так как граф конечен и в нём нет циклов, то процесс закончится только в висячей вершине.

Теорема 3.3. При удалении любого ребра из дерева оно превращается в несвязный граф.

Д о к а з а т е л ь с т в о. Пусть концы удалённого ребра в новом графе соединены цепью. Тогда эта цепь и удалённое ребро образуют цикл.

Теорема 3.4. В дереве число вершин на одну больше числа рёбер.

Д о к а з а т е л ь с т в о. Пусть в графе G n вершин. Предположим v1 – висячая вершина, удалим её и выходящее из неё ребро. После этого опять останется дерево, так как циклов нет.

Пусть v2 – висячая вершина, которую также удалим и т.д. Проделав эту операцию n 1 раз, получим граф, состоящий из одной вершины.

Теорема 3.5. Связный граф G, у которого число рёбер на единицу меньше числа вершин, является деревом.

Д о к а з а т е л ь с т в о. От противного. Пусть G не является деревом, т.е. имеет циклы. Удалив несколько рёбер, можно получить дерево. Тогда число рёбер E и число вершин V удовлетворяют неравенству V E 1. Получили противоречие с теоремой 3.4.

З а д а ч а. Какое наименьшее число рёбер надо удалить из связного графа G, чтобы он оставался связным и в нём не было ни одного цикла?

Решение. Пусть мы удалим ребро графа G n -го порядка e v0, v1, принадлежащее циклу. Граф останется связным, так как от v0 к v1 можно пройти по оставшейся части цикла. Удалим рёбра у оставшихся циклов. Получим в результате дерево G1. Дерево содержит n вершин и n 1 ребро. Пусть N – число рёбер графа G, тогда придётся удалить N n 1 рёбер. Это число называется циклическим порядком графа G.

1. В графе все вершины имеют степень 3. Докажите, что в нём есть цикл.

2. а) В стране n городов и некоторые из них соединены дорогами. При этом любые два города соединяет ровно один путь.

Сколько в этой стране дорог?

б) n точек соединены отрезками так, что любые две точки связывает ровно одна цепочка отрезков. Докажите, что общее число отрезков равно n 1.

3. Волейбольная сетка – прямоугольник 50 600 клеток.

Какое наибольшее число верёвочек можно перерезать, чтобы сетка не распалась?

4. В некоторой стране 30 городов, причём каждый соединён с каждым дорогой. Какое наибольшее число дорог можно закрыть на ремонт так, чтобы из каждого города можно было проехать в каждый другой?

5. В стране 100 городов, некоторые из которых соединены авиалиниями. Известно, что из любого города можно долететь до любого другого (возможно, с пересадками). Докажите, что можно побывать в каждом городе, совершив не более а) 198 перелётов; б) 196 перелётов.

6. Квадрат 8 8 выложили из спичек. Какое наименьшее число спичек надо убрать, чтобы с любого поля можно было пройти на любое другое, не перепрыгивая через спички?

Определение 4.1. Граф называется планарным или плоским, если его можно изобразить на плоскости так, что никакие его два ребра (за исключением рёбер, выходящих из общей вершины) не имеют общих точек.

Граф, изображенный на рис. 13, а, – плоский, а на рис. 13, б – неплоский (см. теорему 4.3).

Определение 4.2. Области, ограниченные ребрами графа, называются гранями.

Число граней обозначим через F, число вершин V, а ребер E.

Теорема 4.1 (Эйлера). Для планарного связного графа имеет место равенство Д о к а з а т е л ь с т в о. Пусть граф G содержит циклы.

Будем удалять ребра, сохраняя связность графа, пока не получим дерево. При этом число вершин V не меняется, а количество ребер уменьшается на одну единицу. Число граней также уменьшается на одну единицу. То есть V E F не меняется.

А для дерева V E 1 и F 1, поэтому V E F 2. Теорема доказана.

Теорема 4.2. Для любого плоского графа 2 E 3F.

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ ГОРНЫЙ УТВЕРЖДАЮ Проректор по научной работе профессор В.Л. ТРУШКО ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ ПО СПЕЦИАЛЬНОЙ ДИСЦИПЛИНЕ СИСТЕМЫ, СЕТИ И УСТРОЙСТВА ТЕЛЕКОММУНИКАЦИЙ, соответствующей направленности (профилю) направления подготовки научно-педагогических кадров в аспирантуре НАПРАВЛЕНИЕ. »

«Министерство образования и науки, молодежи и спорта Украины Севастопольский национальный технический университет Кафедра радиотехники и телекоммуникаций МЕТОДИЧЕСКИЕ УКАЗАНИЯ по самостоятельному изучению дисциплины АНАЛОГОВЫЕ ЭЛЕКТРОННЫЕ УСТРОЙСТВА и выполнению контрольной работы для студентов направления 6.050901 — Радиотехника заочной формы обучения Севастополь 2013 2 УДК 621.375 Методические указания по самостоятельному изучению дисциплины Аналоговые электронные устройства и выполнению. »

«ПРИОРИТЕТНЫЙ НАЦИОНАЛЬНЫЙ ПРОЕКТ ОБРАЗОВАНИЕ РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ В.В. АНДРЕЕВ, А.А. БАЛМАШНОВ, В.И. КОРОЛЬКОВ, О.Т. ЛОЗА, В.П. МИЛАНТЬЕВ ФИЗИЧЕСКАЯ ЭЛЕКТРОНИКА И ЕЕ СОВРЕМЕННЫЕ ПРИЛОЖЕНИЯ Учебное пособие Москва 2008 Инновационная образовательная программа Российского университета дружбы народов Создание комплекса инновационных образовательных программ и формирование инновационной образовательной среды, позволяющих эффективно реализовывать государственные интересы РФ через. »

«Министерство образования и науки Украины Севастопольский национальный технический университет ИССЛЕДОВАНИЕ ПРИЕМНОГО ОБОРУДОВАНИЯ СИСТЕМ СПУТНИКОВОЙ НАВИГАЦИИ Методические указания к лабораторным работам по дисциплине Радиоэлектронные системы для студентов дневной и заочной форм обучения специальности Радиотехника Севастополь – 2009 2 УДК 629.056.8: 656.22 Исследование приемного оборудования систем спутниковой навигации: Методические указания к лабораторным работам по дисциплине. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ДИСТАНЦИОННОЕ ОБУЧЕНИЕ В СРЕДЕ MOODLE 2.3 Методические указания Рязань 2012 Введение Дистанционное обучение – современная форма организации образовательного процесса с применением дистанционных образовательных технологий. Его развитие в последнее время обусловлено ростом числа пользователей сети Интернет, доступностью и качеством открытых образовательных электронных ресурсов. В Рязанском. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ И.Б. Бондаренко, Н.Ю. Иванова, В.В. Сухостат УПРАВЛЕНИЕ КАЧЕСТВОМ ЭЛЕКТРОННЫХ СРЕДСТВ Учебное пособие Санкт-Петербург 2010 Бондаренко И.Б., Иванова Н.Ю., Сухостат В.В. Управление качеством электронных средств. – СПб: СПбГУ ИТМО, 2010. – 211с. В учебном пособии описаны технологии и методы управления качеством электронных средств, а также основы. »

«Титульный лист методических рекомен- -^jffte^ Форма даций и указаний, методических реко- Ф СО ПГУ 7.18.3/40 мендаций, методических указаний Министерство образования и науки Республики Казахстан Павлодарский государственный университет им. С. Торайгырова Кафедра Вычислительная техника и программирование МЕТОДИЧЕСКИЕ УКАЗАНИЯ И РЕКОМЕНДАЦИИ к практическим работам по дисциплине Информационная безопасность телекоммуникационных систем для студентов специальности 050719 радиотехника, электроника и. »

«Министерство образования и науки Российской Федерации Сибирский федеральный университет РАДИОТЕХНИЧЕСКИЕ СИТЕМЫ Методические указания к лабораторным работам Учебно-методическое пособие Красноярск СФУ 2012 УДК 621.391 Радиотехнические системы. Методические указания к самостоятельным занятиям и лабораторным работам: Учебно-методическое пособие / С.П. Панько, А.В. Мишуров – Красноярск: Сиб. федер. ун-т, 2012. – 72 с. Приведено содержание самостоятельно работы студентов и описание выполняемых. »

«Министерство образования и науки Российской федерации Нижегородский государственный университет им. Н.И. Лобачевского Национальный исследовательский университет Кафедра радиотехники ИССЛЕДОВАНИЕ МИКРОКОНТРОЛЛЕРА MSP430F1611 Методические указания к лабораторной работе Нижний Новгород Издательство Нижегородского госуниверситета 2013 УДК 681.3 ББК 32.973.2 Исследование микроконтроллера MSP430F1611: Методические указания к лабораторной работе / Сост. — Н.Новгород: ННГУ, 2013- с. Методические. »

«База нормативной документации: www.complexdoc.ru 4.3. МЕТОДЫ КОНТРОЛЯ. ФИЗИЧЕСКИЕ ФАКТОРЫ Порядок подготовки и оформления санитарно-эпидемиологических заключений на передающие радиотехнические объекты Методические указания МУ 4.3.2320-08 1. Разработаны: Управлением Федеральной службы по надзору в сфере защиты прав потребителей и благополучия человека по г. Москве (В.Я. Ицков, И.А. Веретина, Г.Н. Жичкина); ФГУЗ Центр гигиены и эпидемиологии в городе Москве Роспотребнадзора (Е.А. Руднева, А.А. »

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Видео:7 класс, 23 урок, Примеры задач на построениеСкачать

На плоскости дано 100 окружностей

§ 23. Метод геометрических мест точек в задачах на построение

Известно, что если смешать синий и жёлтый цвета, то получим зелёный.

Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а жёлтым — обладающие вторым свойством, то понятно, что зелёные точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами.

Задача 1. Постройте треугольник по трём данным его сторонам.

Решение. Пусть даны три отрезка, длины которых равны a , b , c (рис. 327). Надо построить треугольник ABC , в котором AB = c , AC = b , BC = a .

Проведём произвольную прямую. С помощью циркуля отложим на ней отрезок CB , равный a (рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки A .

Воспользуемся тем, что точка A обладает сразу двумя свойствами:

1) принадлежит геометрическому месту точек, удалённых от точки B на расстояние c , т. е. окружности с центром в точке B радиуса с (см. рис. 328);

2) принадлежит геометрическому месту точек, равноудалённых от точки C на расстояние b , т. е. окружности с центром в точке С радиуса b (см. рис. 328).

В качестве точки A можно выбрать любую из двух образовавшихся зелёных точек.

Полученный треугольник ABC является искомым, так как в нём AB = c , AC = b , BC = a .

Из описанного построения следует, что если каждый из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.

Задача 2. Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии a от его вершины.

Решение. Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным a .

Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка X .

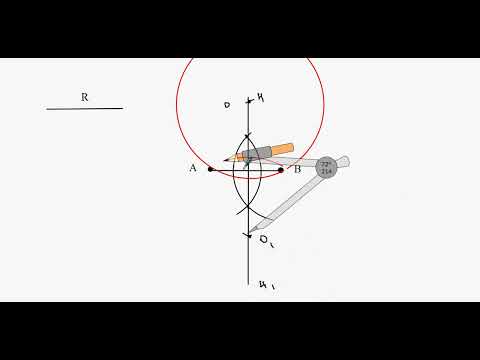
Задача 3. Постройте центр окружности радиуса R , проходящей через данную точку M и касающуюся данной прямой a .

Решение. Поскольку окружность касается прямой a , то её центр находится на расстоянии R от этой прямой. Геометрическим местом точек, удалённых от данной прямой на данное расстояние, являются две параллельные прямые (см. упражнение 498). Следовательно, центр окружности находится на прямой b или на прямой с (рис. 330).

Геометрическое место точек, являющихся центрами окружностей радиуса R , проходящих через точку M , — это окружность данного радиуса с центром в точке M . Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения окружности с одной из прямых b или с (рис. 331).

Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно.

Задача 4. Постройте треугольник по стороне, медиане, проведённой к этой стороне, и радиусу описанной окружности.

Решение. Построим окружность данного радиуса и проведём хорду AB , равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности и окружности с центром в точке O , являющейся серединой хорды AB , и радиусом, равным данной медиане. Каждый из треугольников ABС 1 и ABС 2 (рис. 332) является искомым. Поскольку эти треугольники равны, то задача имеет единственное решение.

622. Даны прямая m и точки A и B вне её (рис. 333). Постройте на прямой m точку, равноудалённую от точек A и B .

623. Точки A и B принадлежат прямой m . Постройте точку, удалённую от прямой m на расстояние a и равноудалённую от точек A и B . Сколько решений имеет задача?

624. Точки B и C принадлежат разным сторонам угла A , причём АВ ≠ АС . Постройте точку M , принадлежащую углу, равноудалённую от его сторон и такую, что MB = MC .

625. Точки B и C принадлежат разным сторонам угла A . Постройте точку D , принадлежащую углу, равноудалённую от его сторон и такую, что DC = BC . Сколько решений может иметь задача?

626. Постройте равнобедренный треугольник по основанию и боковой стороне.

627. Для данной окружности постройте точку, являющуюся её центром.

628. Постройте окружность данного радиуса, проходящую через данную точку, центр которой принадлежит данной прямой.

629. Постройте окружность данного радиуса, проходящую через две данные точки.

630. Найдите все точки, принадлежащие данной окружности и равноудалённые от концов данного отрезка. Сколько решений может иметь задача?

631. Даны две пересекающиеся прямые m и n и отрезок AB . Постройте на прямой m точку, удалённую от прямой n на расстояние AB . Сколько решений имеет задача?

632. В треугольнике ABC известно, что ∠ C = 90°. На катете AC постройте точку D , удалённую от прямой AB на расстояние CD .

633. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности. Сколько решений может иметь задача?

634. Постройте треугольник по двум сторонам и медиане, проведённой к одной из данных сторон.

635. Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к боковой стороне.

636. На данной окружности постройте точку, находящуюся на данном расстоянии от данной прямой. Сколько решений может иметь задача?

637. На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача?

638. Между двумя параллельными прямыми дана точка. Постройте окружность, проходящую через эту точку и касающуюся данных прямых. Сколько решений имеет задача?

639. Постройте окружность, проходящую через данную точку A и касающуюся данной прямой m в данной точке B .

640. Даны две параллельные прямые и секущая. Постройте окружность, касающуюся этих трёх прямых.

641. Постройте треугольник по двум сторонам и радиусу описанной окружности. Сколько решений может иметь задача?

642. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и радиусу описанной окружности. Сколько решений может иметь задача?

643. Постройте равносторонний треугольник по радиусу описанной окружности.

644. Три прямые попарно пересекаются и не проходят через одну точку. Постройте точку, равноудалённую от всех трёх прямых. Сколько решений имеет задача?

645. Постройте прямоугольный треугольник по катету и сумме гипотенузы и другого катета.

646. Постройте прямоугольный треугольник по гипотенузе и сумме катетов.

647. Постройте прямоугольный треугольник по гипотенузе и разности катетов.

648. Постройте прямоугольный треугольник по катету и разности гипотенузы и другого катета.

649. Постройте равнобедренный треугольник по основанию и разности боковой стороны и высоты, опущенной на основание.

650. Постройте треугольник по стороне, прилежащему к ней углу и сумме двух других сторон.

651. Постройте треугольник по стороне, прилежащему к ней углу и разности двух других сторон.

652. Постройте треугольник по стороне, противолежащему ей углу и разности двух других сторон.

653. Постройте треугольник по стороне, противолежащему ей углу и сумме двух других сторон.

654. Постройте треугольник по стороне, разности углов, прилежащих к этой стороне, и сумме двух других сторон.

655. Постройте треугольник по периметру и двум углам.

656. Постройте остроугольный треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла.

657. Постройте треугольник по высоте и медиане, проведённым из одной вершины, и радиусу описанной окружности.

658. Постройте треугольник по двум сторонам и медиане, проведённой к третьей стороне.

659. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и медиане, проведённой к одной из двух других сторон.

Упражнения для повторения

660. На рисунке 334 ∠ A = 46°, ∠ ACB = 68°, ∠ DEC = 120°. Найдите углы треугольников EFC и DBE .

661. Через середину O стороны MK треугольника MKN провели прямую, перпендикулярную стороне MK и пересекающую сторону MN в точке C . Известно, что MC = KN , ∠ N = 50°. Найдите угол MCO .

662. В треугольнике ABC из вершины прямого угла C провели высоту CH и биссектрису CM . Длина отрезка HM в 2 раза меньше длины отрезка CM . Найдите острые углы треугольника ABC .

663. На рисунке 335 BD = DC , DN ⊥ BC , ∠ BDM = ∠ MDA . Найдите сумму углов MBN и BMD .

Наблюдайте, рисуйте, конструируйте, фантазируйте

664. Разрежьте фигуру, изображённую на рисунке 336, на три части, не являющиеся квадратами, так, чтобы из этих частей можно было сложить квадрат.

Когда сделаны уроки

Из истории геометрических построений

Умение достигать результат, используя минимальные средства, всегда считалось признаком высокого мастерства. Видимо, поэтому в Древней Греции в значительной степени было развито искусство выполнять геометрические построения с помощью только двух инструментов: дощечки с ровным краем (линейки) и двух заострённых палочек, связанных на одном конце (циркуля). Такое ограничение в выборе инструментов историки связывают с древнегреческой традицией, считавшей прямую и окружность самыми гармоничными фигурами. Так, в своей книге «Начала» великий учёный Евклид описывал построения геометрических фигур, при которых использовались лишь циркуль и линейка.

Существует много задач на построение. С некоторыми из них вы уже успели познакомиться. Однако есть три задачи на построение, которые сыграли в развитии математики особую роль. Эти задачи стали знаменитыми.

Задача о квадратуре круга. Построить квадрат, площадь которого равна площади данного круга.

Задача о трисекции угла (от латинских tria — «три» и section — «разрезание») . Разделить угол на три равные части.

Задача об удвоении куба. Построить куб, объём которого в 2 раза больше объёма данного куба.

Эти задачи занимали умы людей на протяжении тысячелетий. Их пытались решить и такие выдающиеся учёные древности, как Гиппократ Хиосский, Евдокс Книдский, Евклид, Эратосфен, Аполлоний Пергский, Герон, Папп, Платон, Архимед, и гении Нового времени Рене Декарт, Франсуа Виет, Исаак Ньютон. И лишь в середине XIX века была доказана их неразрешимость, т. е. невозможность выполнить указанные построения с использованием лишь циркуля и линейки. Этот результат был получен средствами не геометрии, а алгебры, благодаря переводу этих задач на язык уравнений.

Когда вы решали задачи на построение, особенно те, которые отмечены знаком , вы, по-видимому, испытали сложности, связанные с ограниченностью набора инструментов. Поэтому предложение ещё больше сузить возможности применяемых приборов может показаться вам по меньшей мере неожиданным. Однако ещё в Х веке персидский математик Мохаммед Абу-ль-Вефа описал решение целого ряда задач на построение с помощью линейки и циркуля, раствор которого нельзя было менять. Совсем удивительной является теорема, опубликованная в 1797 году итальянским математиком Лоренцо Маскерони (1750–1800): всякое построение, выполнимое циркулем и линейкой, можно проделать одним циркулем. При этом Маскерони обусловливал следующее: поскольку одним циркулем провести прямую нельзя, то прямая считается построенной, если построены какие-нибудь две её точки.

В ХХ веке была обнаружена книга датского учёного Георга Мора (1640–1697), в которой он также описал построения одним циркулем. Поэтому сформулированную выше теорему называют теоремой Мора — Маскерони.

Видео:Окружность и задачи на построениеСкачать

Задачи на тему «Геометрия».
Программирование на Си, С++ (консольные приложения).

Их список будет расти.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность через три точки

Определить радиус и центр окружности, проходящей, по крайней мере, через три различные точки заданного множества точек на плоскости и содержащей внутри наибольшее количество точек этого множества.

Из школьного курса известно, что через любые три точки (если только они не лежат на одной прямой) можно провести окружность. Строится серединный перпендикуляр для первых двух точек, т.к. центр окружности будет лежать только на нем (обеспечена равноудаленность). А его пересечение со вторым серединным перпендикуляром даст точку — центр окружности, которая будет равноудалена до всех трех заданных точек.

Пусть пользователь задает только количество точек, а их координаты будут генерироваться случайно.

Впрочем, в тестовом варианте, надо дать возможность явно указывать координаты некоторых точек

Вот результат, после того как пользователь ввел число 25.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Прямая пересекающая окружности

На плоскости заданы множества точек A и множество окружностей B.
Найти две различные точки из A такие, чтобы проходящая через них прямая пересекалась с максимальным количеством окружностей из B.

В цикле по каждым двум точкам находим уравнение прямой.
Затем, во вложенном цикле, определяем расстояние до этой прямой от каждого центра окружности и сравниваем с ее радиусом.
И становится понятно, пересекает прямая окружность или нет

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Параллельность прямых

На плоскости задано множество точек А и множество прямых В.
Найти две различные точки из А такие, чтобы проходящая через них прямая была параллельна наибольшему количеству прямых из В.

Ну, здесь еще проще: после того как по паре точек определили уравнение прямой остается сравнить коэффициенты наклона полученной прямой со всеми прямыми из множества В.

Видео:Бестселлер Все правила по геометрии за 7 классСкачать

Точки на сторонах треугольников

Среди треугольников с вершинами в заданном множестве точек на плоскости указать такой, стороны которого содержат максимальное число точек заданного множества.

Определить, лежит ли точка на «прямой» по уравнению прямой задача считай дошкольная
А сравнив координаты вершин треугольника и выбранной точки, можно однозначно сказать, лежит ли она на стороне треугольника или за пределами
Остается подсчитать все это в циклах и запоминать наилучший вариант из просмотренных.

Видео:Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать

Площадь выпуклого многоугольника

Однотипность этих задач видна невооруженным взглядом
Поэтому, структуры данных и многие функции, несущие явную геометрическую направленность, выделены в отдельный модуль.
Не сомневаюсь, он пригодится мне еще не раз
Да и Вам, наверное, тоже

Если у Вас остались вопросы, то задать их Вы можете, нажав на эту кнопочку .