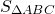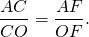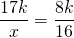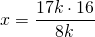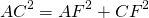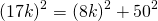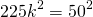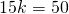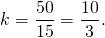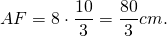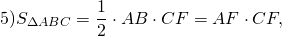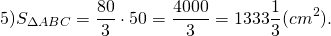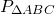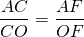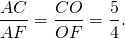Центр вписанной в равнобедренном треугольнике окружности может лежать

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

We are checking your browser. mathvox.ru

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:№690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружностиСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d5f9c8b2cac7b47 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Тест по геометрии для 8 класса

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Центр описанной окружности равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

по геометрии для 8 класса

1.Центр вписанной в треугольник окружности совпадает с точкой пересечения его …

в) серединных перпендикуляров.

2. Центр вписанной в треугольник окружности равноудален от …

в) вершин треугольника.

3. Центр вписанной в треугольник окружности является точкой пересечения его медиан. Этот треугольник…

4. Окружность называется вписанной в многоугольник, если…

а) все его стороны касаются окружности;

б) все его вершины лежат на окружности;

в) все его стороны имеют общие точки с окружностью.

по геометрии для 8 класса

1. Радиус вписанной в треугольник окружности равен расстоянию от центра окружности до …

а) сторон треугольника;

б) вершин треугольника;

в) углов треугольника.

2. Центр вписанной в равнобедренный треугольник окружности может лежать…

а) на любой из его высот;

б) на любой из его медиан;

в) на любом из его серединных перпендикуляров.

3. Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Этот треугольник может быть…

б) только равносторонним;

в) только прямоугольным.

4. Многоугольник называется описанным около окружности, если …

а) окружность имеет общие точки с его сторонами;

б) окружность проходит через его вершины;

в) окружность является касающейся всех его сторон.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 942 человека из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 517 099 материалов в базе

Другие материалы

• 17.03.2017
• 1450
• 19

• 17.03.2017
• 1181
• 0

• 17.03.2017
• 5037
• 16

• 17.03.2017
• 792
• 2

• 17.03.2017
• 376
• 0

• 17.03.2017
• 266
• 0

• 17.03.2017
• 299
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 17.03.2017 6609
• DOCX 13.1 кбайт
• 11 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Еленкина Алена Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 11 месяцев
• Подписчики: 10
• Всего просмотров: 47339
• Всего материалов: 19

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Школьники Чебоксар с 27 января перейдут на дистанционный формат обучения

Время чтения: 1 минута

Школы Северной Осетии переведут на дистанционное обучение

Время чтения: 1 минута

Онлайн-семинар о снятии эмоционального напряжения у детей и подростков

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Центр вписанной окружности равнобедренного ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Где лежит центр описанной окружности? 1 задание ЕГЭ ПрофильСкачать

Окружность, вписанная в равнобедренный треугольник

Если в задача дана окружность, вписанная в равнобедренный треугольник, в ее решении могут быть использованы свойства касательных и свойство биссектрисы треугольника.

Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию .

Рассмотрим две задачи на вписанную в равнобедренный треугольник окружность.

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 8:9, считая от вершины угла при основании треугольника. Найти площадь треугольника, если радиус вписанной окружности равен 16 см.

окружность (O, r) — вписанная,

F, K, M, — точки касания со сторонами AB, BC, AC,

1) Пусть k — коэффициент пропорциональности (k>0). Тогда AM=8k см, MC=9k см.

2) По свойству касательных, проведенных из одной точки,

AF=AM=8k см, CK=MC=9k см.

Так как AC=BC, то BK=AM и BF=BK=8k см.

3) Центр вписанной окружности является точкой пересечения биссектрис треугольника.

Так как ∆ ABC — равнобедренный с основанием AB, то CF — высота, медиана и биссектриса ∆ ABC.

4) Рассмотрим треугольник AFC.

∠AFC=90, AF=8k см, AC=AM+MC=17k см.

OF=r. Пусть CO=x см, тогда

CO=34 см, CF=CO+OF=34+16=50 см.

По теореме Пифагора:

Ответ: 1333 1/3 кв.см.

Центр окружности, вписанной в равнобедренный треугольник, делит высоту, проведенную к основанию, в отношении 5:4. Найти периметр треугольника, если боковая сторона меньше основания на 15 см.

Дано: ∆ ABC, AC=BC,

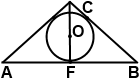
окружность (O, r) — вписанная,

CF — высота, CO:OF=5:4, AC

1) Рассмотрим ∆ ACF — прямоугольный (так как CF — высота треугольника по условию).

Центр вписанной в треугольник окружности есть точка пересечения его биссектрис.

По свойству биссектрисы треугольника,

Пусть k — коэффициент пропорциональности, тогда AC=5k см, AF=4k см, AB=2AF=8k см.

Следовательно, AC=BC=5∙5=25 см, AB=8∙5=40 см.

🔥 Видео

Свойство окружности, описанной около равнобедренного треугольникаСкачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

ЕГЭ Математика Задание 6#27935Скачать

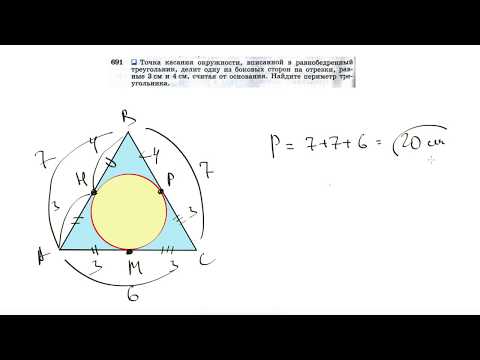
№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать

Геометрия Центр окружности, вписанной в равнобедренный треугольник, делит его высоту, проведеннуюСкачать

Задание 26 Равнобедренный треугольник Вписанная окружностьСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Геометрия Радиус окружности вписанной в равнобедренный треугольник, составляет 2/9 высотыСкачать

Планиметрия 28 | mathus.ru | Радиус окружности, вписанной в равнобедренный треугольникСкачать

Задание 26 Окружность Равнобедренный треугольникСкачать

ОГЭ Задание 26 Треугольник Вписанная окружность ПлощадьСкачать