На рисунке 1 прямые a и b параллельны так как

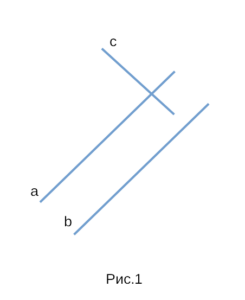
Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).

Определение 1. Две прямые на плоскости называются параллельными , если они не пересекаются.

Если прямые a и b параллельны, то это обозначают так:

.

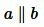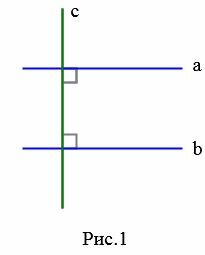
На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).

Понятие параллельности можно распространять и на отрезки.

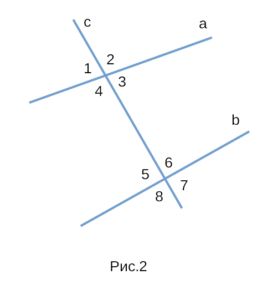
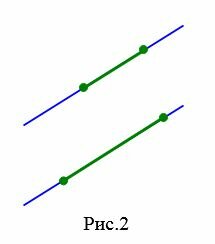
Определение 2. Два отрезка называются параллельными , если они лежат на параллельных прямых (Рис.2).

Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.

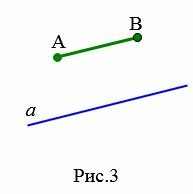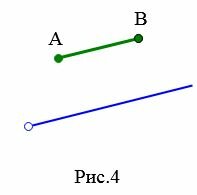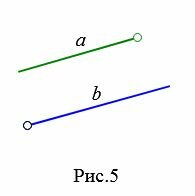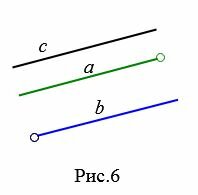На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.

Видео:№186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что a||b, если: a)∠1=37°Скачать

Признаки параллельности прямых

Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):

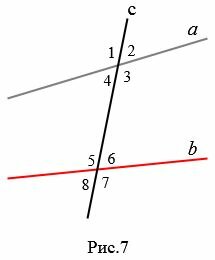• накрест лежащие углы: 3 и 5, 4 и 6;
• односторонние углы: 4 и 5, 3 и 6;
• соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Определим признаки параллельности двух прямых, связанные с этими парамы углов.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).

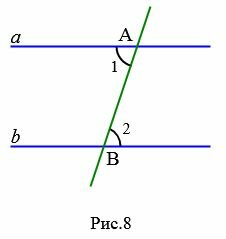Докажем, что .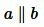

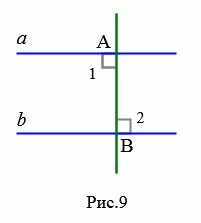
Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).

Предположим, что углы 1 и 2 не прямые (Рис.10).

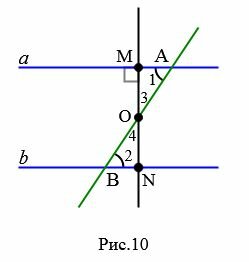Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .

означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны.

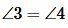
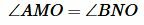
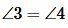
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).

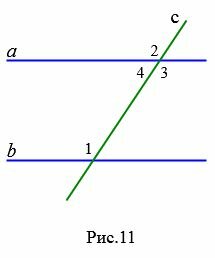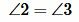
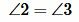
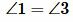
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

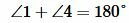
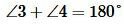
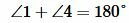
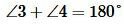
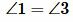
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.

Видео:№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

Параллельные прямые

Определение

Параллельными прямыми называются две прямые,
которые не пересекаются.

Параллельность прямых обозначают знаком: ∥. Например
параллельность прямых a и b обозначается так: a ∥ b.

На рисунке 1 изображены три прямые. Прямая а параллельна
прямой b, прямая c не параллельна ни одной из прямых.

Также, как и параллельные прямые, существуют параллельные
отрезки. Два отрезка называются параллельными, если они
лежат на параллельных прямых.

Признаки

Параллельность двух прямых можно доказать по трем признакам.

На рисунке 2 изображены 8 углов, при помощи которых можно
доказать все три признака параллельности. Это накрест лежащие
углы: 3 и 5, 4 и 6; односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Прямая называется секущей по отношению к двум другим прямым,
если она пересекает их в двух точках.

1. Если при пересечении двух прямых секущей
   накрест лежащие углы равны, то прямые параллельны.
2. Если при пересечении двух прямых секущей
   соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей
   сумма односторонних углов равна 180°, то прямые параллельны.

Видео:№ 186 - Геометрия 7-9 класс АтанасянСкачать

Геометрия. 7 класс

Соответственные углы

Выберите правильный ответ. Найдите на рисунке соответственные углы.

Выберите правильный ответ из выпадающего списка

Укажите, верно утверждение или нет.

1. ∠7 и ∠8 – односторонние
2. ∠3 и ∠ 8 – накрест лежащие
3. ∠ 1 и ∠ 8 – соответственные

Признаки параллельности прямых

Установите соответствие между признаком параллельности прямых и рисунком, иллюстрирующим его.

Прямые a и b параллельны, так как накрест лежащие углы равны

Прямые a и b параллельны, так как сумма односторонних углов равна 180°

Прямые a и b параллельны, так как соответственные углы равны

Как называются углы, изображенные на рисунке? Добавьте подписи к изображениям.

Аксиома параллельных прямых

Выберите все правильные ответы.

Через точку, не лежащую на данной прямой, проходит:

бесчисленное множество прямых пересекающихся с данной

только одна прямая, параллельная данной

всегда проходит прямая, параллельная данной

Найдите углы

Выделите цветом правильный ответ.

На рисунке a ǁ b, ∠1 на 32° меньше ∠3. Найдите ∠2.

Расстояние между прямыми

Подчеркните правильный ответ. Прямые AC и BD параллельны. Точка K удалена от прямой AC на 3,5 см, а от прямой BD на 5,5 см. Найдите длину отрезка CD.

Перпендикулярные прямые

Введите с клавиатуры правильный ответ.

На рисунке a ┴ c, b ┴ c. Тогда прямые a и b – .

Биссектриса внешнего угла

Докажите утверждение: если биссектриса внешнего угла параллельна одной из его сторон, то треугольник равнобедренный.

Так как AE ǁ BC , то ∠B = ∠DAE, это углы
Так как AE ǁ BC, то ∠ C = ∠CAE, это углы
AE – биссектриса, значит ∠CAE =
Следовательно, ∠B = ∠С, т. к. углы при основании ∆ равны, значит ∆ABC –	Градусные меры углов Введите верные значения. По рисунку определите градусную меру следующих углов: Докажите Докажите, что m ǁ n и найдите ∠1. Выберите верные ответы. Так как , значит m ǁ n, l секущая. ∠1 = °. Прямые и углы Выделите цветом верный ответ. На рисунке прямые а и b параллельны, AB =AC, ∠1 = 68°. Тогда ∠2 равен: Градусная мера угла Введите с клавиатуры результат вычислений. Найдите градусную меру ∠BCD. На рисунке AB ǁ DE, ∠CBA = 112°, ∠CDE = 164°. Докажите утверждение Восстановите порядок доказательства. Ниже приведена схема доказательства утверждения: если точка О – середина отрезков EL и FK, то прямые EF и KL параллельны. ∠EOF = ∠LOK по свойству вертикальных углов. Из равенства треугольников следует, что ∠OEF = ∠OLK накрест лежащие. ∆EOK = ∆LOK по 1 признаку равенства треугольников. Значит, прямые EF и KL параллельны по признаку параллельности прямых. 🔍 Видео №202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать 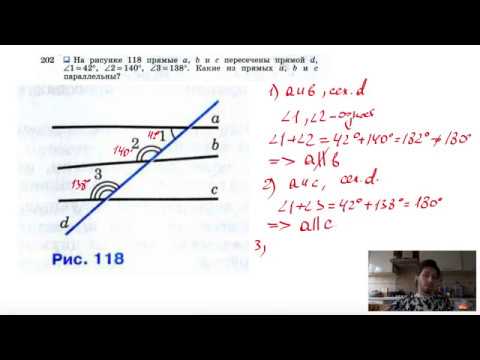№209. На рисунке 118 a||b, c||d, ∠4=45°. Найдите углы 1, 2 и 3.Скачать №200. На рисунке 115 AD||p и PQ||BC. Докажите, что прямая р пересекает прямые АВ, АЕ, АС, ВС и PQ.Скачать №204 Концы отрезка АВ лежат на параллельных прямых а и b. Прямая, проходящая через середину ОСкачать Параллельные прямые | Математика | TutorOnlineСкачать №203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать Задачи. Признак параллельности прямых. Доказать, что прямые параллельны. По рисунку.Скачать 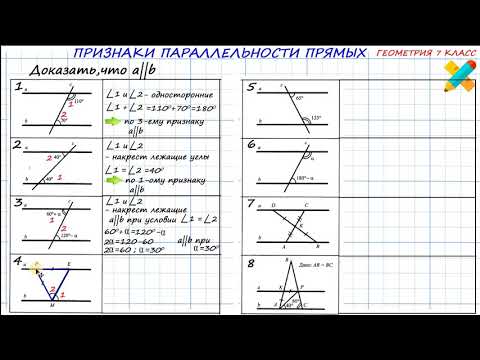Параллельные прямые (задачи).Скачать №282. Прямые а и b параллельны. Докажите, что середины всех отрезков XY, где Х∈а, Y∈bСкачать Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать №558. Прямые а и b пересечены параллельными прямыми АА1, BB1, CC1, причем точки А, В и ССкачать Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать №198. Прямые а и b перпендикулярны к прямой р, прямая с пересекает прямую а. ПересекаетСкачать решение задач на параллельность прямыхСкачать №93. Прямые а и b параллельны. Через точку М прямой a проведена прямая MN, отличная от прямой а и неСкачать 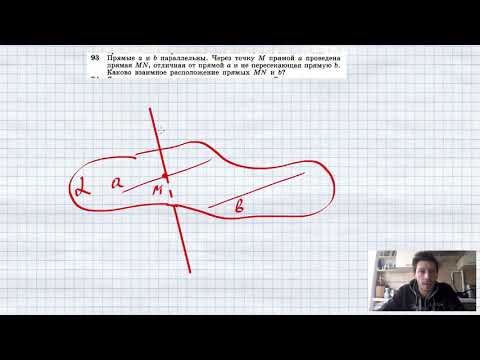№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать 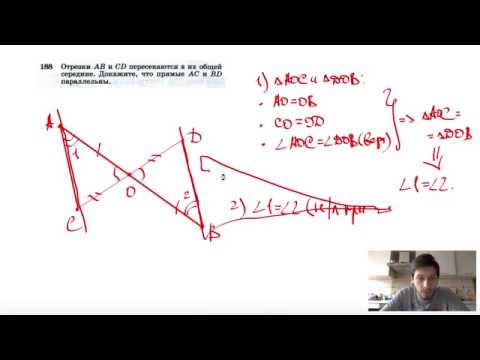Поделиться или сохранить к себе: Смотрите также 2 параллельные прямые пересекаются 3 прямой найди углы сумма которых данным углом равна 180 градусов 2 параллельные прямые пересечены 3 прямой то внутренние накрест лежащие углы равны 2 прямые параллельны одной и той же плоскости можно ли утверждать что эти прямые Четырехугольник у которого противолежащие стороны параллельны то есть лежат на параллельных прямых 1 вписанный угол опирающийся на полуокружность острый 2 если две параллельные прямые пересечены 1 даны 2 параллельные прямые и секущая построить окружность касающуюся всех 3 х прямых 1 из внутренних односторонних углов образованных при пересечении 2 параллельных прямых 3 прямой 1 из односторонних углов образованных при пересечении 2 параллельных прямых секущей в 4 раза больше