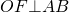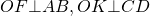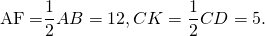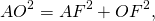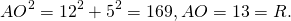Как найти расстояние от хорды до окружности

Рассмотрим, как найти расстояние от центра окружности до хорды.

Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.

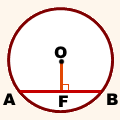
Например, расстояние от точки O — центра окружности — до хорды AB равно длине перпендикуляра OF:

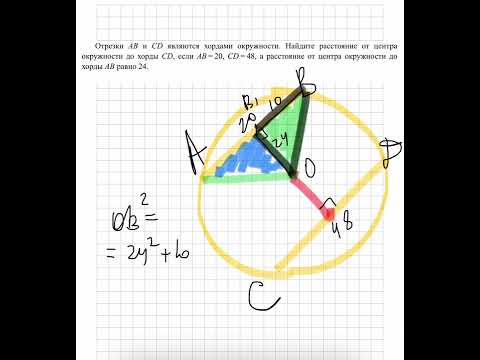
Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10, а расстояние от центра окружности до хорды AB равно 5.

Дано: окружность (O; R), AB и CD — хорды,

1) Соединим центр окружности с концами хорд.

2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).

Значит, их высоты OF и OK являются также медианами. Следовательно,

3) Рассмотрим треугольник AOF, где ∠AFO=90 º.

4) Рассмотрим треугольник COK, где ∠CKO=90 º.

Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Видео:Как найти диаметр окружности, зная длину хорды и расстояние от центра окружности до неё? #огэ #егэСкачать

Найти расстояние от хорды до окружности

Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Расстояние от центра окружности до хорды

Рассмотрим, как найти расстояние от центра окружности до хорды.

Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.

Например, расстояние от точки O — центра окружности — до хорды AB равно длине перпендикуляра OF:

Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10, а расстояние от центра окружности до хорды AB равно 5.

Дано: окружность (O; R), AB и CD — хорды,

1) Соединим центр окружности с концами хорд.

2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).

Значит, их высоты OF и OK являются также медианами. Следовательно,

3) Рассмотрим треугольник AOF, где ∠AFO=90 º.

4) Рассмотрим треугольник COK, где ∠CKO=90 º.

Видео:ОГЭ 2022 Демоверсия. 16 заданиеСкачать

Найти расстояние от хорды до окружности

Видео:Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать

Определение хорды

Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности

Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .

Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.

Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.

Видео:Длина окружности. Математика 6 класс.Скачать

Свойства хорды к окружности

• Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
• Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
• Наибольшая возможная хорда является диаметром
• Серединный перпендикуляр к хорде проходит через центр окружности

• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу

• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
• Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Свойства хорды и вписанного угла

Видео:Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.Скачать

Свойства хорды и центрального угла

Видео:Задача на нахождение длины хорды окружностиСкачать

Формулы нахождения хорды

Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде

Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.

Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

Решение задач

Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.

Задача.

Решение.

Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x

Согласно свойству хорд AS x SB = CS x SD, тогда

2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10

Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10

Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то

3,5х + 5,5х + 3х = 360
12х = 360
х = 30

Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165

Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:

90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5

Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;

🎥 Видео

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать

Как найти длину хорды по радиусу и центральному углу. Геометрия 8-9 классСкачать

Окружность. Длина хорды. Теорема синусов.Скачать

16)Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия на ЕГЭ. Расстояние от центра окружности до произвольной точки хорды. Степень точки.Скачать

Геометрия Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 5Скачать