Формула площади сферического треугольника (5 видео)

Формула площади сферического треугольника

§ 28. Сферический треугольник и основные формулы сферической тригонометрии

Многие задачи астрономии, связанные с видимыми положениями и движениями небесных тел, сводятся к решению сферических треугольников.

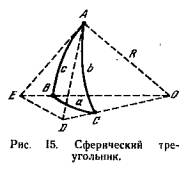
Сферическим треугольником называется фигура АВС на поверхности сферы, образованная дугами трех больших кругов (рис. 15).

Углами сферического треугольника называются двугранные углы между плоскостями больших кругов, образующих стороны сферического треугольника. Эти углы измеряются плоскими углами при вершинах треугольника между касательными к его сторонам.

Обычно рассматриваются треугольники, углы и стороны которых меньше 180°. Для таких сферических треугольников сумма углов всегда больше 180°, но меньше 540°, а сумма сторон всегда меньше 360°. Разность между суммой трех углов сферического треугольника и 180° называется сферическим избытком s , т.е.

s = Р A + Р B + Р C — 180°.

Площадь сферического треугольника s равна

где R — радиус сферы, на поверхности которой образован треугольник.

Сферический треугольник, таким образом, отличается по своим свойствам от плоского, и применять к нему формулы тригонометрии на плоскости нельзя.

Возьмем сферический треугольник АВС (рис. 15), образованный на сфере радиуса R и с центром в точке О.

Из вершины А проведем касательные AD и АЕ к сторонам b и с до пересечения их с продолжениями радиусов ОС и 0В, лежащих в одной плоскости с соответствующей касательной. Соединив прямой точки пересечения D и Е, получим два плоских косоугольных треугольника ADE и ODE с общей стороной DE . Применяя к этим треугольникам теоремы элементарной геометрии, напишем:

DE 2 = OD 2 + ОЕ 2 — 2 OD Ч ОЕ Ч cos a,

DE 2 = AD 2 + АЕ 2 — 2 AD Ч АЕ Ч cos A.

Вычитанием второго равенства из первого получим:

2 OD Ч ОЕ Ч cos a = OD 2 — AD 2 + ОЕ 2 — АЕ 2 + 2 AD Ч АЕ Ч cos A.

Из прямоугольных плоских треугольников ОАЕ и ОА D следует:

OD 2 — AD 2 = R 2 ; OE 2 — AE 2 = R 2 ;

Подставив эти соотношения в формулу (1.31) и произведя соответствующие сокращения и переносы, получим

cos а = cos b cos с + sin b sin с cos A ,

т.е. косинус стороны сферического треугольника равен произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними.

Формулу (1.32) можно написать для любой стороны треугольника. Напишем ее, например, для стороны b :

cos b = cos с cos a + sin с sin a cos B

и, подставив в нее cos сх из формулы (1.32), получим

cos b = cos с (cos b cos с + sin b sin с cos A) + sin с sin a cos B.

Раскрыв скобки и перенеся первый член правой части в левую, будем иметь:

cos b (l — cos 2 с) = sin b sin с cos с cos A + sin c sin a cos B.

Заменив (1 — cos 2 с) на sin 2 с и сократив все на sin c , окончательно получим

sin a cos В = sin c cos b — cos c sin b cos A,

т.е. произведение синуса стороны на косинус прилежащего угла равняется произведению синуса другой стороны, ограничивающей прилежащий угол, на косинус третьей стороны минус произведение косинуса стороны, ограничивающей прилежащий угол, на синус третьей стороны и на косинус угла, противолежащего первой стороне.

Формула (1.33) называется формулой пяти элементов. Ее можно написать по аналогии и для произведений sin a cos С, sin b cos A , sin b cos С, sin с cos A и sin с cos В.

Решим теперь равенство (1.32) относительно cos A :

Возведя обе части последнего равенства в квадрат и вычтя их из 1, получим:

Раскрыв скобки и разделив обе части этого выражения на sin 2 а, получим

Полученное выражение совершенно симметрично относительно a , b и с, и заменяя A на В, а на b или A на С и а на с, напишем

Содержание

Формула площади сферического треугольника
Сферические треугольники решение и формулы (Таблица)
Сферические треугольники.
Свойства сферических треугольников.
🎥 Видео

Видео:МОС. ЛР 7.Скачать

Формула площади сферического треугольника

Во всей истории науки нет ничего более революционного, чем развитие неевклидовых геометрий, которое до основания потрясло веру в то, что теория Евклида является вечной истиной.

Эдвард Каснер и Джеймс Ньюмен («Математика и воображение», 1941)

Все мы знаем множество геометрических понятий, потому что постоянно используем этот раздел математики в нашей повседневной жизни. Но эти понятия относятся к так называемой «классической», или «евклидовой», геометрии. Однако существуют другие геометрии, которые устроены совсем не так, как нас учили в школе. Эта книга не сделает вас специалистом в нетрадиционных геометриях, зато покажет, что реальность гораздо богаче, чем кажется на первый взгляд.

В этой книге описаны другие способы мышления и отношения к геометрии, способы, отличающиеся от тех, которые прочно укоренились в нашей повседневной жизни, и которые определяют наши действия в соответствии с евклидовой геометрией. Можно подумать, что новые геометрии понятны лишь великим ученым, но мы постараемся в последующих главах в наиболее ясной и понятной форме изложить их основы.

Возможно, самым простым способом открытия новых миров является попытка увидеть их проявления в более понятных и очевидных сферах нашей повседневной жизни. Таким образом, наше изложение начнется с короткого путешествия в «геометрию такси», которая основана на так называемом «расстоянии Минковского», отличающемся от расстояния в обычном понимании. Как бы мы ни хотели улететь в дальние экзотические страны, для начала мы должны не терять землю под ногами. Нам придется обратиться к Евклиду, чтобы понять, как основные элементы геометрии используются в повседневной жизни. Лишь тогда мы сможем перейти к обсуждению таких понятий, как «пятый постулат» и «проблема параллелей», из которых рождаются интересующие нас новые геометрии.

Лишь владея лучшими инструментами математической теории, мы можем вступить в мир новых геометрий. Сначала проведем разведку, чтобы узнать, как обстоят дела. Мы рассмотрим различные попытки доказательства пятого постулата. Ведь только в XVIII в. непоколебимое на протяжении столетий учение Евклида было наконец поставлено под сомнение самыми выдающимися математиками того времени.

Неудачные попытки доказать пятый постулат поставили под сомнение, казалось бы, неоспоримые основы традиционной геометрии. В это время и проявили себя одни из самых замечательных ученых в области математики. История альтернативных интерпретаций пятого постулата является в равной мере историей неудач и гениальных открытий. С ней связаны самые известные в истории математики имена: Лобачевский, Бойяи, Гаусс, Риман… Мы более подробно рассмотрим удивительные результаты первой из новых геометрий — гиперболической геометрии Лобачевского и Бойяи. Мы увидим, как она кардинально изменила наше понимание физической реальности и как она повлияла на исследования Альберта Эйнштейна и открытие им теории относительности.

Эллиптическая геометрия Римана перенесет нас в удивительный мир сфер, где у треугольников сумма внутренних углов больше 180°. Мы воспользуемся сферической геометрией, чтобы ответить на многие вопросы. Что является кратчайшим расстоянием между двумя городами на поверхности Земли? Можно ли измерить внутренние углы треугольника, вершинами которого являются Париж, Лондон и Мадрид? Решения этих геометрических задач оказываются весьма полезными в нашем глобализованном мире, где GPS позволяет определить координаты любой точки нашей планеты.

Словно река, прорвавшая древнюю плотину, новые идеи смели традиционные научные понятия и породили сотни новых. Мы коснемся также геометрии XXI в. — интегральной и вычислительной геометрии, являющейся основой новых технологий.

Читатели, желающие поглубже изучить эти вопросы, найдут в конце книги список литературы. Алфавитный указатель позволит легко ориентироваться в тексте книги.

Поездка на такси

Нам часто приходится в повседневной жизни измерять предметы. Математическую дисциплину, изучающую такие задачи, древние греки называли геометрией. Это слово происходит от греческого geometrein, где geo означает «земля», a metrein — «измерять». Когда мы говорим о геометрии, мы всегда используем единственное число.

Казалось бы, множественное число — геометрии — подразумевает существование целого ряда возможных дисциплин на выбор. Такой подход звучит слишком заумно, эта идея находится за пределами понимания обычных людей. Тем не менее, так оно и есть: другие геометрии существуют.

Разве ученые абсолютно точно знают, что такое на самом деле точка в пространстве или прямая линия, проходящая через нее? Может ли круг иметь форму прямоугольника? Знаем ли мы, что означает «параллельность»?

Ответы на эти вопросы не являются вечными истинами, а меняются на протяжении времени. Евклид с полной убежденностью утверждал, что «через точку вне прямой можно провести только одну прямую, параллельную данной», но Лобачевский показал, что можно провести много параллельных прямых, практически бесконечное число. Риман был не согласен с обоими и считал, что параллельные прямые не существуют. Кто же из этих великих математиков прав? Может, все они правы?

Или они все ошибаются?

В данной главе мы как раз и разрешим все эти неопределенности, но, пожалуй, нам лучше начать с простого примера, который наглядно демонстрирует, почему возникает путаница относительно самой природы физической реальности.

Отправляясь из дома на работу или в другое место, мы вычисляем время, которое потребуется на дорогу, исходя из расстояния. Но часто оказывается, что расчеты не соответствуют реальному времени. Пробки, светофоры, дорожные работы — список таких задержек можно продолжать бесконечно. Все это, казалось бы, идет наперекор нашим тщательным планам.

Проблема заключается в том, что мысленно мы моделируем наше путешествие геометрически идеальным образом, представляя наш путь в виде почти прямой линии. Однако реальность вовсе не является геометрически идеальной. Наши расчеты нарушают не только неисправные светофоры или разгружающие товары грузовики. Дело еще и в том, что блоки городских зданий не образуют идеальных квадратов, а улицы не пересекаются под идеально прямыми углами… Означает ли это, что невозможно найти оптимальную дорогу, чтобы утром добраться до работы?

ИЛЬДЕФОНСО СЕРДА (1815–1876)

Известный главным образом как инженер и архитектор, Ильдефонсо Серда обладал многими талантами, занимаясь также экономикой, правом и политикой. Его реформа городского планирования в Барселоне в XIX в., получившая название «План Серда», изменила лицо города, в результате чего появился один из самых впечатляющих районов — Эшампле. По-каталонски (I’Eixample) или по-испански (el Ensanche) это означает «расширение». Улицы Эшампле образуют прямоугольные кварталы, пересекаясь на равных расстояниях друг от друга.

Вид с воздуха на район Эшампле в Барселоне.

Как и следовало ожидать, реальность никогда не бывает геометрически идеальной, иначе бы мир был очень скучным, представляя из себя утомительные повторения упорядоченных форм. Однако рациональность и упорядоченность являются важными критериями, которые необходимо учитывать на практике, например, в городском планировании. По вполне разумным причинам улицы многих современных городов образуют квадратные блоки. Одним из первых примеров такого городского планирования был район Эшампле в испанском городе Барселоне, детище архитектора Ильдефонсо Серда. Этот район послужит идеальным вводным примером к нашей теме.

Видео:9. Площадь сферического треугольникаСкачать

Сферические треугольники решение и формулы (Таблица)

Сферические треугольники.

На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара, и сферической поверхности. Сторонами а, b, с сферического треугольника называют те углы между лучами, которые меньше 180°. Каждой стороне треугольникасоответствует дуга большого круга на поверхности шара (рис. 1). Углы A, В, С сферического треугольника, противолежащие сторонам а, b, с соответственно, представляют собой, по определению, меньшие, чем 180°, углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лучами.

Свойства сферических треугольников.

Каждая сторона и угол сферического треугольника по определению меньше 180°. Геометрия на поверхности шара является неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360°, сумма углов заключена между 180° и 540°. В каждом сферическом треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс третий угол.

Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):