Все свойства окружности вписанной и описанной для огэ

теория по математике 📈 планиметрия

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Описанная окружность

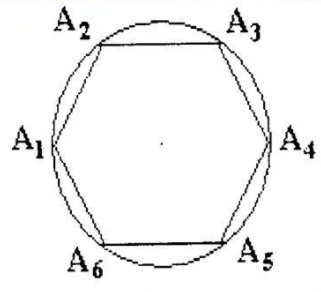
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная окружность

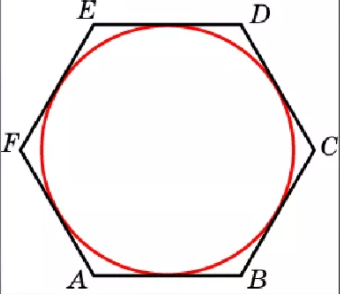
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 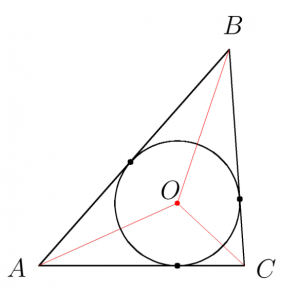Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

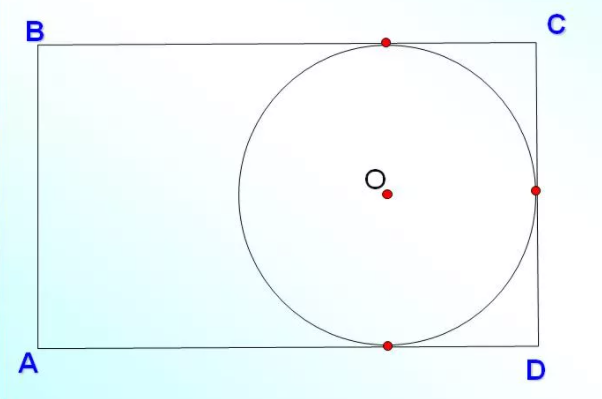
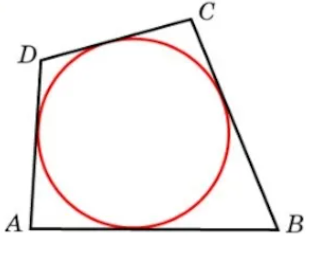
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

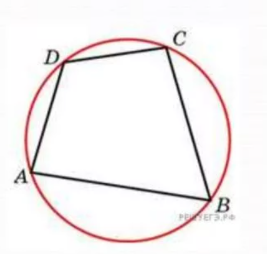
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Видео:Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Видео:Все о вписанных и описанных окружностях с нуля | PARTAСкачать

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Видео:16 задание ОГЭ математика 2023 | УмскулСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Вписанные и описанные окружности. Подготовка к ОГЭ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Имыкшенова Л.Ю., подготовка к ОГЭ

Вписанные и описанные окружности

Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30 0 . Найдите сторону AB этого треугольника.

Решение:
Если вписанный угол 30 0 , то дуга АВ=60 0 . Центральный угол АОВ равен дуге, на которую он опирается 60 0 . Треугольник АОВ равнобедренный, АО=ВО, как радиусы одной окружности. Углы при основании равны (180-60):2 = 60. Значит, треугольник равносторонний. АО=ВО=АВ=3.
Ответ: 3.

Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.

Решение:
Треугольник АОВ равносторонний, т.к. сторона АВ равна радиусу описанной окружности. Центральный угол АОВ=60 0 , тогда дуга, на которую он опирается 60 0 . Вписанный угол равен половине дуги, на которую он опирается 30 0 .

Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 30º. Найдите радиус окружности, описанной около этого треугольника.

Решение:
Если вписанный угол 30 0 , то дуга АВ=60 0 . Центральный угол АОВ равен дуге, на которую он опирается 60 0 . Треугольник АОВ равнобедренный, АО=ВО, как радиусы одной окружности. Углы при основании равны (180-60):2 = 60. Значит, треугольник равносторонний. АО=ВО=АВ=1.
Ответ: 1.

Найдите высоту трапеции, в которую вписана окружность радиуса 1.

Решение:
Простое дополнительное построение позволит нам увидеть диаметр окружности. Этот отрезок для трапеции является высотой. Ответ: 2.

Найдите сторону квадрата, описанного около окружности радиуса 4.

Решение:
a ₄ = 2r Если вы не помните эту формулу связывающую r и a (радиус вписанной окружности и сторону квадрата). Не беда. Вы можете сделать дополнительное построение и увидеть это. Ответ: 8.

Найдите радиус окружности, вписанной в квадрат со стороной 4.

Решение:
Конечно, формулу надо знать a ₄ = 2r Но, те, кто «не дружит, с формулами, могут выполнить простенькое дополнительное построение и увидеть, что радиус вписанной окружности равен половине стороны квадрата. Ответ: 2.

Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Решение:
Кто знает формулу a ₆ = R, найдут ответ мгновенно. Кто не знает или сомневается, могут выполнить дополнительное построение. Посмотрите на треугольник ВОС, он равносторонний. Сторона правильного шестиугольника равна радиусу описанной окружности. Ответ: 6.

Найдите сторону квадрата, вписанного в окружность радиуса

Решение:
Конечно, авторы задания мечтали, что дети знают формулу (или ) и смогут быстро получить ответ: . Ответ: 4. Но возможно вы найдете сторону квадрата из треугольника АВС через sin45 0 или cos45 0 или даже по теореме Пифагора, обозначив равные катеты в треугольнике АВС через «x».

Найдите радиус окружности, описанной около квадрата со стороной, равной

Решение:
Применим формулу (или )

Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.

Решение:
Построим диагональ. Центр описанной около прямоугольника окружности – точка пересечения диагоналей. Ответ: 10.

Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 3 и 4.

Решение:
Построим диагональ. Треугольник АВС – египетский, значит, диагональ 5. Диагональ является и диаметром, значит, радиус 2,5.

Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120º. Найдите диаметр описанной окружности этого треугольника.

Решение:
Треугольники АОС и и АОВ равносторонние (обоснуйте самостоятельно). Значит, радиус равен 1. Диаметр равен 2.

В треугольнике ABC ВС=6, угол C равен 90º. Радиус описанной окружности этого треугольника равен 5. Найдите AC.

Решение:
На рисунке обозначен прямой угол, значит, он опирается на диаметр, АВ =10. Значит, второй катет – 8 (Египетский треугольник со сторонами 3, 4 и 5, пропорциональные стороны: 6, 8 и 10). А может, вы посчитаете неизвестный катет по теореме Пифагора.

В треугольнике АВС АС = 4, ВС = 3, угол С равен 90º. Найдите радиус описанной окружности этого треугольника.

Решение:
На рисунке обозначен прямой угол, значит, он опирается на диаметр. Треугольник с катетами 3 и 4 – египетский, значит гипотенуза равна5. Радиус равен половине гипотенузы 5:2 = 2,5.
Ответ: 2,5.

Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника.

Решение:
На рисунке обозначен прямой угол, значит, он опирается на диаметр. Радиус 4, значит, диаметр 8.
Ответ: гипотенуза 8.

Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.

Решение:
На рисунке обозначен прямой угол, значит, он опирается на диаметр. Гипотенуза равна 12, значит, диметр 12, а радиус 6.
Ответ: радиус 6.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Все о вписанной окружности для ЕГЭ и ОГЭ. Теория с примерами.Скачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 512 892 материала в базе

Другие материалы

• 22.04.2017
• 659
• 0

• 22.04.2017
• 1198
• 0

• 22.04.2017
• 1167
• 0

• 22.04.2017
• 1268
• 0

• 22.04.2017
• 1723
• 8

• 22.04.2017
• 461
• 0

• 22.04.2017
• 3363
• 2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 22.04.2017 4614
• DOCX 366.8 кбайт
• 91 скачивание
• Рейтинг: 1 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Имыкшенова Лилия Юрьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 4657
• Всего материалов: 1

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Вписанные и описанные окружности. Задание №16 | PARTA МАТЕМАТИКА ОГЭ 2023Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Все школы Ненецкого АО перевели на удаленку

Время чтения: 1 минута

Школы Пскова перевели на дистанционное обучение

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Большинство российских вузов используют смешанный формат обучения

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📸 Видео

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Хитрости в решении геометрических задач в ОГЭ по математике | Математика TutorOnlineСкачать

Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать

ВПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать