Базисные вектора оцк решетки

Видео:Лекция 9. Кристаллические решетки. Элементарная ячейка.Скачать

1.1. Аморфные и кристаллические тела

В твердых телах атомы могут размещаться в пространстве двумя способами:

Беспорядочное расположение атомов, когда они не занимают определенного места друг относительно друга. Такие тела называются аморфными .

Аморфные вещества обладают формальными признаками твердых тел, т.е. они способны сохранять постоянный объем и форму. Однако они не имеют определенной температуры плавления или кристаллизации.

Упорядоченное расположение атомов, когда атомы занимают в пространстве вполне определенные места, Такие вещества называются кристаллическими .

Атомы совер­шают относительно своего среднего положения колебания с частотой около 10 13 Гц . Амплитуда этих колебаний пропорциональна температуре .

Благодаря упорядоченному расположению атомов в про­странстве, их центры можно соединить воображаемыми прямыми ли­ниями. Совокупность таких пересекающихся линий представ­ляет пространственную решетку, которую называют кристаллической решеткой .

Внешние электронные орбиты атомов сопри­касаются, так что плотность упаковки атомов в кристаллической решетке весьма велика.

Кристаллические твердые тела состоят из кристаллических зерен — кристал­литов. В соседних зернах кристаллические решетки поверну­ты относительно друг друга на некоторый угол.

В кристаллитах соблюдаются ближний и дальний порядки. Это означает на­личие упорядоченного расположения и стабильности как ок­ружающих данный атом ближайших его соседей (ближний порядок), так и ато­мов, находящихся от него на значительных расстояниях вплоть до границ зерен (дальний порядок ).

Рис. 1.1. Расположение атомов в кристаллическом (а) и аморфном (б) веществе

Вследствие диффузии отдельные атомы могут по­кидать свои места в узлах кристаллической решетки, однако при этом упорядоченность кристаллического строения в целом не на­рушается.

Видео:Самый простой способ понять ХИМИЮ — Типы Кристаллических Решеток и Свойства ВеществаСкачать

1.2. Основные типы кристаллических решеток

Все металлы являются кристаллическими телами, имею­щими определенный тип кристаллической решетки, состоящей из малоподвижных положительно заряженных ионов, между которыми движутся свободные электроны (так называемый электронный газ). Такой тип структуры называется металлической связью.

Тип ре­шетки определяется формой элементарного геометриче­ского тела, многократное повторение которого по трем пространственным осям образует решетку данного кристал­лического тела.

(1 атом на ячейку)

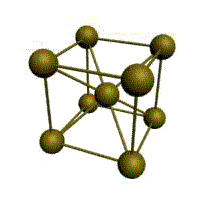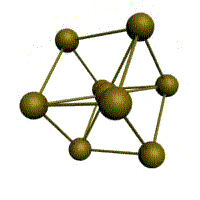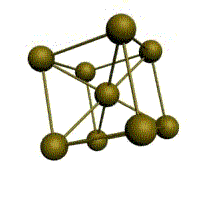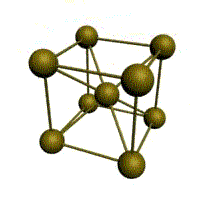
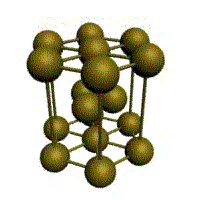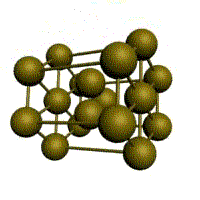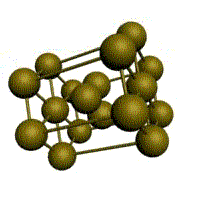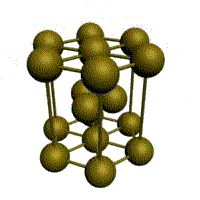
объемно-центрированная кубическая (ОЦК)

(2 атома на ячейку)

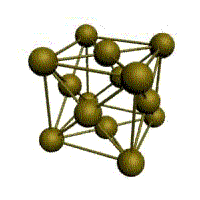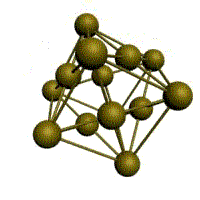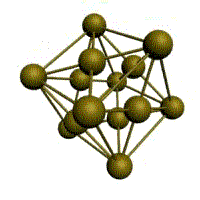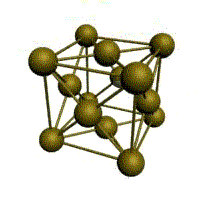
гранецентрированная кубическая (ГЦК)

(4 атома на ячейку)

гексагональная плотноупакованная (ГП)

(6 атомов на ячейку)

Рис. 1.2. Основные типы кристаллических решеток металлов

Металлы имеют относительно сложные типы кубических ре­шеток — объемно центрированная (ОЦК) и гранецентриро­ванная (ГЦК) кубические решетки.

Основу ОЦК-решетки составляет элементарная кубиче­ская ячейка (рис. 1.2,б), в которой положительно заряжен­ные ионы металла находятся в вершинах куба, и еще один атом в центре его объема, т. е. на пересечении его диагоналей. Такой тип решетки в определенных диапазонах температур имеют железо, хром, ванадий, вольфрам, молибден и др. металлы.

У ГЦК-решетки (рис. 1.2, в) элементарной ячейкой слу­жит куб с центрированными гранями. Подобную решетку имеют железо, алюминий, медь, никель, свинец и др. металлы.

Третьей распространенной разновидностью плотноупако­ванных решеток является гексагональная плотноупакованная (ГПУ, рис. 1.2, г). ГПУ-ячейка состоит из отстоя­щих друг от друга на параметр с параллельных центриро­ванных гексагональных оснований. Три иона (атома) нахо­дятся на средней плоскости между основаниями.

У гексагональных решеток отношение параметра с/ а всегда больше единицы. Такую решетку имеют маг­ний, цинк, кадмий, берилий, титан и др.

Компактность кристаллической решетки или степень за­полненности ее объема атомами является важной характе­ристикой. Она определяется такими показателями как параметр решетки, число атомов в каждой элементарной ячейке, координационное число и плотность упаковки.

Параметр решетки — это рас­стояние между атомами по ребру эле­ментарной ячейки. Параметры решетки измеряется в нанометрах (1 нм = 10 -9 м = 10 Å ). Параметры куби­ческих решеток характеризуются длиной ребра куба и обозначаются буквой а.

Для характеристики гексагональной решетки прини­мают два параметра — сторону шестигранника а и высоту призмы с. Когда отношение с/а = 1,633, то атомы упакованы наиболее плотно, и решетка называется гек­сагональной плотноупакованной (рис. 1.2 г). Некоторые металлы имеют гексагональную решетку с менее плотной упаковкой атомов (с/а > 1,633). Напри­мер, для цинка с/а = 1,86, для кадмия с/а = 1,88.

Параметры а кубических решеток металлов находятся в пределах от 0,286 до 0,607 нм. Для металлов с гексагональной решеткой а лежит в пределах 0,228-0,398 нм, а с в пределах 0,357- 0,652 нм.

Пара­метры кристаллических решеток металлов могут быть измерены с по­мощью рентгеноструктурного анализа.

При подсчете числа атомов в каждой элементарной ячейке следует иметь в виду, что каждый атом входит одновременно в несколько яче­ек. Например, для ГЦК-решетки, каждый атом, находящийся в вершине куба, принадлежит 8 ячейкам, а атом, центрирующий грань, двум. И лишь атом, находящийся в центре куба, полностью при­надлежит данной ячейке.

Таким образом, ОЦК- и ГЦК-ячейки содержат соответ­ственно 2 и 4 атома.

Под координационным числом понимается количество ближайших соседей данного атома.

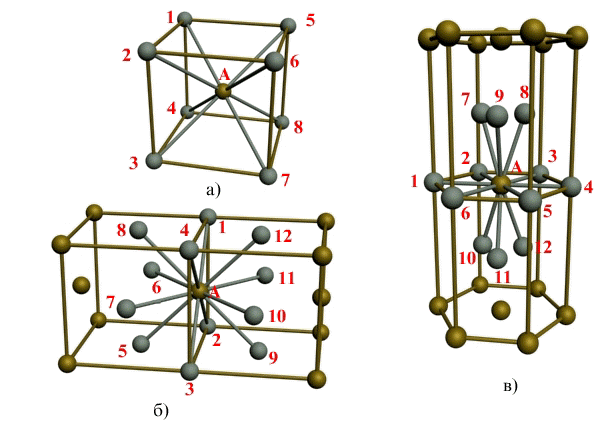
Рис. 1.3. Координационное число в различных кристаллических решетках для атома А:

а) — объемноцентрированная кубическая (К8); б) — гранецентрированная ку­бическая (К12); в) — гексагональная плотноупакованная (Г12)

В ОЦК решетке (рис. 1.3, а) атом А (в центре) находится на наиболее близ­ком равном расстоянии от восьми атомов, расположенных в вершинах куба, т. е. координационное число этой решетки равно 8 (К8).

В ГЦК решетке (рис. 1.3, б) атом А (на грани куба) находится на наиболее близком равном расстоянии от четырех атомов /, 2, 3, 4, расположенных в вершинах куба, от четырех атомов 5, 6, 7, 8, расположенных на гранях куба, и, кроме того, от четырех атомов 9, 10, 11, 12, принадлежащих располо­женной рядом кристаллической ячейке. Атомы 9, 10, 11, 12 симметричны атомам 5, 6, 7, 8. Таким образом, ГЦК решетки координацион­ное число равно 12 (К12).

В ГПУ решетке при с/а = 1,633 (рис. 1.3, в) атом А в центре шестигранного основания призмы находится на наиболее близком равном расстоянии от шести атомов /, 2, 3, 4, 5, 6, размещенных в вершинах шестигранника, и от трех атомов 7, 8, 9, расположенных в средней плоскости призмы. Кроме того, атом А оказывается на таком же расстоянии еще от трех атомов 10, 11, 12, принадлежащих кристаллической ячейке, лежащей ниже основания. Атомы 10, 11, 12 симметричны атомам 7, 8, 9.

Следовательно, для ГПУ решетки координационное число равно 12 (Г12).

Плотность упаковки представляет собой отношение сум­марного объема, занимаемого собственно атомами в кристал­лической решетке, к ее полному объему. Различные типы кристаллических решеток имеют раз­ную плотность упаковки атомов. В ГЦК решетке атомы занимают 74 % всего объема кристаллической решетки, а межатом­ные промежутки («поры») 26 %. В ОЦК решетке атомы занимают 68 % всего объема, а «поры» 32 %. Компактность решетки за­висит от особенностей электронной структуры металлов и ха­рактера связи между их атомами.

От типа кристаллической решетки сильно зависят свойства металла.

Видео:Как разложить вектор по базису - bezbotvyСкачать

1.3. Кристаллографические направления и плоскости

Упорядоченность кристаллического строения в пространственной решетке позволяет выделить отдельные кри­сталлографические направления и плоскости.

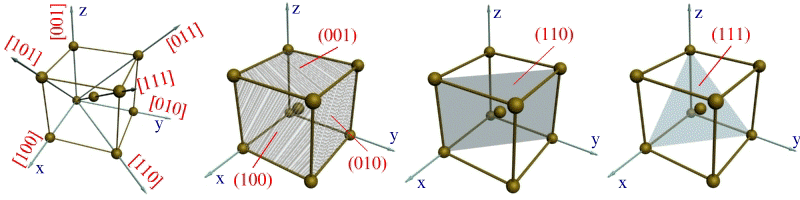
Кристаллографические направления — это характерные прямые линии, выходящие из точки отсчета, вдоль которых в кристаллической решетке располагаются атомы. Точками отсчета, могут служить вершины куба, а кристаллографическими направле­ниями — его ребра и диагонали, а также диагонали граней (рис. 1.4, а).

Рис. 1.4. Кристаллографические направления и плоскости в кри­сталлической решетке: а) — основные направления и их обозначе­ние; б), в), г) — основные плоскости и их обозначение

Кристаллографическими плоскостями являются, напри­мер, плоскости граней кубов (рис. 1.4, б), а также их раз­личные диагональные плоскости вместе с находящимися на них атомами (рис. 1.4, в, г). Для ГПУ-ре­шеток кристаллографическими плоскостями могут быть плоскости оснований (рис. 1.2, г).

Для определения индекса какого-либо направления необ­ходимо найти индекс ближайшего к данной точке отсчета атома, находящегося на данном направлении. На­пример, индекс ближайшего атома вдоль оси ОХ обозначает­ся цифрами 100 (рис. 1.4,а). Эт и цифры представляют собой координаты упомянутого атома относи­тельно точки О, выраженные через количество параметров вдоль осей OX, OY и OZ соответственно.

Индексы направления ОХ и параллельных ему направле­ний обозначаются [100]. Соответственно направления OY и OZ обозначаются [010] и [001]. Кристаллографические направления вдоль диагоналей граней XOZ, XOY и YOZ обозначают [101], [110] и [011]. Пользуясь указанной мето­дикой, можно определить индекс любого направления. На­пример, индекс направления вдоль диагонали куба выразит­ся так: [111].

Для определения индекса кристаллографической плоско­сти необходимо вначале найти координаты ближайших точек ее пересечения с осями координат, проведенными из точки отсчета О. Затем взять обратные им величины и записать их в круглых скобках в обычной последовательности. Напри­мер, координатами точек пересечения с осями координат бли­жайшей плоскости, параллельной плоскости XOY, выражен­ными через параметры решеток, являются числа Ґ , Ґ , 1 (см. рис. 1.4, б). Поэтому индекс этой плоскости можно запи­сать в виде (001).

Индексами плоскостей, параллельных плоскостям XOZ и YOZ, окажутся выражения (010) и (100) (рис. 1.4, б). Индекс вертикальной диагональной плоскости куба выразит­ся через (110), (рис. 1.2, в), а индекс наклонной плоско­сти, пересекающейся со всеми тремя осями координат на уда­лении одного параметра, примет вид (111) (см. рис. 1.4, г).

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

1.4. Анизотропия в кристаллах

Под анизотропией понимается неодинаковость механиче­ских и других свойств в кристаллических телах вдоль раз­личных кристаллографических направлений. Она является естественным следствием кристаллического строения, так как на различных кристаллографических плоскостях и вдоль различных направлений плотность атомов различна.

Например, в куби­ческих решетках (см. рис. 1.2, б, в) по направлениям вдоль ребер насчитывается меньше атомов, чем вдоль диагоналей куба в ОЦК-решетке или диагоналей граней в ГЦК-решетке. На плоскостях, проходящих через грани ОЦК- и ГЦК-решеток, находится меньше атомов, чем на диагональных плоскостях.

Поскольку механические, физические и химические свойства вдоль различных направлений зависят от плотности находя­щихся на них атомов, то перечисленные свойства вдоль раз­личных направлений в кристаллических телах должны быть неодинаковыми.

Анизотропия проявляется только в пределах одного монокристалла или зерна-кри­сталлита. В поликристаллических телах она не наблюдается из-за усреднения свойств по каждому направлению для огром­ного количества произвольно ориентированных друг относи­тельно друга зерен. Поэто­му реальные металлы являются квазиизотропными телами, т. е. псевдоизотропными.

Рис. 1.5. Элементарная ячейка решетки ОЦК

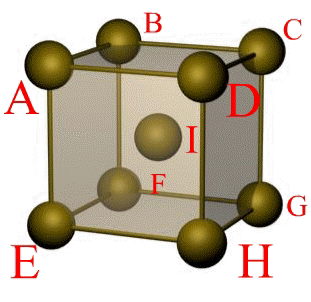
Сдвиг в кристалле происходит наиболее легко вдоль атомных плоскостей с наиболее плотной упаковкой атомов. Рассмотрим объемно-центрическую кубическую решетку (ОЦК) (рис. 1.5):

1) Плоскость ABCD (рис 1.6 а) . Количество атомов в плоскости ABCD – 1; площадь ABCD = a 2 ; площадь, приходящаяся на 1 атом – удельная площадь: – мера плотности упаковки.

Рис. 1.6. Плоскости решетки ОЦК

а) — базисная плоскость; б) — плоскость с максимальной упаковкой атомов

2) Плоскость ABGH (рис 1.6 б) . Количество атомов в плоскости ABGH – 2; площадь ABGH = a 2 ;

В плоскости ABGH плотность упаковки больше чем в AB С D . Наиболее вероятен сдвиг вдоль диагональных плоскостей.

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

1.5. Аллотропия металлов

Некоторые металлы, например, железо, титан, олово и др. способны по достижении определенных темпера­тур изменять кристаллическое строение, т. е. изменять тип элементарной ячейки своей кристаллической решетки. Это явление получило название аллотропии или полиморфизма, а сами переходы от одного кристаллического строения к дру­гому называются аллотропическими или полиморфными.

На рис. 1.7 показано изменение свободной энергии F от температуры t для двух вариантов кристаллического строения же­леза: ОЦК (кривая 1 ) и ГЦК (кривая 2).

В интервале температур 911-1392 о C железо имеет решетку ГЦК, так как при этом его свободная энергия меньше. При t 1392°С, у него должна быть ре­шетка ОЦК, обладающая меньшей свободной энергией.

Рис. 1.7. Изменение свободной энергии (F_св) в зависимости от температуры (T) и типа кристал­лической решетки: 1 — для ОЦК-решетки; 2 — для ГЦК-решетки

Разные аллотропические формы металлов обозначают­ся буквами греческого алфавита, при этом низкотемператур­ные модификации обозначаются буквой a , а последующие в порядке роста температур — буквами b, g ,d и т. д. Аллотропическими формами железа являются: до 911°С — альфа-же­лезо ( a -Fe), имеющее ОЦК-решетку, от 911°С до 1392 °С -гамма-железо ( g -Fe) с решеткой ГЦК и от 1392°С до 1539 °С т. е. до температуры плавления — снова a -Fe с решеткой OЦK, однако, чтобы отличить его от низкотемпературной модификации, его принято называть дельта-железом ( d -F е).

Известное в практике так называемое немагнитное бета-железо ( b -Fe) самостоятельной аллотропической формой не является, так как имеет такую же, как у a -Fe ОЦК-решетку и отличается от него только отсутствием магнитных свойств, которые оно теряет при 768°С (точка Кюри).

Видео:Кристаллические решетки: заучить или понять за 20 минут? | Химия ЕГЭ 2023 | УмскулСкачать

1.6. Дефекты кристаллической решетки металла

Кристаллическая решетка, в которой отсутствуют нарушения сплошности и все узлы заполнены однородными атомами называется идеальной кристалли­ческой решеткой металла.

В решетке реального металла могут находиться различные дефекты.

Все дефекты кристаллической решетки принято делить на точечные, линейные, поверхностные и объемные.

Точечные дефекты соизмеримы с размерами атомов. К ним относятся вакансии, т. е. незаполненные узлы решет­ки, межузельные атомы данного металла (рис 1.8), примесные атомы замещения, т. е. атомы, по диаметру соизмеримые с атомами данного металла и примесные атомы внедрения, имеющие очень малые размеры и поэтому находящиеся в междоузлиях (рис 1.9). Влияние этих дефектов на прочность металла может быть различным в зависимости от их ко­личества в единице объема и характера.

Рис. 1.8. Схема образования пары вакансия-внедренный атом

Рис. 1.9. Примесные атомы внедрения и замещения

Линейные дефекты имеют длину, значительно превышаю­щую их поперечные размеры. К ним относятся дислокации, т. е. дефекты, образующиеся в решетке в результате смещений кристаллографических плоскостей.

Дислокации бывают двух видов.

Наиболее характерной является краевая дислокация (рис. 1.10). Она образуется в результате возникновения в решетке так называемой полуплоскости или экстраплоскости.

Рис. 1.10. Схема краевой дислокации в идеальном кристалле

Нижний ряд экстраплоскости собственно и принято называть дислокацией.

Другим типом дислокации является винтовая дислокация, которая представляет собой некоторую условную ось внутри кристалла, вокруг которой закручены атомные плоскости (рис.1.11).

Рис. 1.11. Схема винтовой дислокация

В винтовой дислокации, так же как в краевой, существенные искажения кристаллической решетки наблюдаются только вблизи оси, поэтому такой дефект может быть отнесен к линейным.

Дислокации обладают высокой подвижностью, поэтому существенно уменьшают прочность металла, так как облегчают образование сдвигов в зернах-кристаллитах под действием приложенных напряжений.

Дислокационный механизм сдвиговой пластической деформации внутри кристаллов может привести к разрушению изделия. Таким образом, дислокации непосредственно влияют на прочностные характеристики металла.

Для оценки этого влияния используется плотность дислокаций, под которой принято по­нимать отношение суммарной длины дислокаций к объему содержащего их металла. Плотности дислокаций измеряется в см -2 или м -2 .

На рис. 1.12 в виде кривой ABC схематически показана за­висимость прочности металла от плотности дислокаций. Точ­ка А соответствует теоретической прочности металла, обус­ловленной необходимостью одновременного разрыва всех межатомных связей, проходящих через плоскость сдвига, в случае отсутствия дислокаций.

При увеличении количества дислокаций (см. участок АВ) прочность резко снижается, так как на несколько порядков уменьшаются усилия, необходимые для осущест­вления сдвигов в зернах металла при его деформировании и разрушении.

Рис. 1.12. Зависимость предела прочности кристалла от плотности линейных дефектов(дислокаций). Кривая Одинга

При плотности дислокаций 10 6- 10 7 см-2 (точ­ка В на кривой), прочности минимальна, и на участке ВС происходит ее рост. Это объясняется тем, что с ростом плотности дислокаций их передвижение происходит не только по парал­лельным, но и по пересекающимся плоскостям, что существенно затрудняет процесс деформирования зерен.

Поэтому начиная с точки В прочность металла возрастает.

Максимальная плотность дислокаций, может составить 10 13 см -2 . При дальнейшем росте плотности дислокаций происходит разрушение металла.

Поверхностные дефекты включают в себя главным образом границы зерен (рис.1.13). На границах кристаллическая решетка сильно искажена. В них скапливаются перемещающиеся изнутри зерен дислокации.

Из практики известно, что мелкозернистый металл прочнее круп­нозернистого. Так как у последнего меньше суммарная про­тяженность (площадь) границ. То можно сделать вывод, что поверхностные дефекты способствуют повышению прочности металла. Поэтому создано несколько технологических способов полу­чения мелкозернистых сплавов.

Рис.1.13. Структура границы двух соседних кристаллических зерен

Объемные дефекты кристаллической решетки включают трещины и поры. Наличие данных дефектов, уменьшая плотность металла, снижает его прочность.

Кроме того, трещины являются сильными концентратора­ми напряжений, в десятки и более раз повышающими напря­жения создаваемые в металле рабочими нагрузками. По­следнее обстоятельство наиболее существенно влияет на прочность металла.

Видео:Кристаллические решетки металлов | Матвед 1Скачать

Контрольные вопросы по лекции №1

В чем состоит существенная разница между строением аморфных и кристаллических тел? Что такое кристаллическая решетка?

Перечислите основные типы ячеек кристаллических решеток металлов. Что такое параметры решеток?

Что понимается под кристаллографическими направлениями и плоскостями и как они обозначаются?

Что такое анизотропия свойств в кристаллах, чем она обусловлена? Привести пример.

Почему поликристаллические тела являются изотропными? Что такое квазиизотропия (псевдоизотропия)?

Что такое аллотропия (полиморфизм) металлов и ка­ково ее практическое значение?

Что представляют собой краевые дислокации, какова их роль в протекании пластической деформации металла и как они влияют на его прочность?

Что такое плотность дислокаций и как она влияет на характер изменения прочности металла?

Видео:Кристаллические решетки.Скачать

Кристаллическая решетка. Решетки Бравэ и с базисом. Обозначения узлов, направлений и плоскостей в кристаллах (индексы Миллера)

Твердое тело с регулярной правильной структурой в расположении атомов в пространстве называется кристаллом. Для описания правильной внутренней структуры кристаллов вводят понятие кристаллической решетки. Различают трансляционные решетки Бравэ и решетки с базисом.

Решетка Бравэ. С геометрической точки зрения правильное периодически повторяющееся размещение частиц в кристалле можно описать с помощью операции параллельного перемещения, или трансляции. Перенос частицы вдоль оси ОХ декартовой системы координат на отрезки а, 2а, . та, вдоль оси ОУ на отрезки Ь, 2Ь. нЬ, вдоль оси OZ на отрезки с, 2с, . рс, где т,п,р — целые числа, есть операция трансляции. Положение любой частицы в такой решетке определяется вектором

где а,Ь,с — наименьшие векторы трансляции, их абсолютные значения есть периоды трансляции.

Решетка, построенная путем параллельного переноса (трансляции) какого-либо узла (точки, где кончается вектор г, начинающийся в начале произвольно выбранной системы декартовых координат) по трем направлениям, называется трансляционной решеткой, или решеткой Бравэ.

Наименьший параллелепипед, построенный на векторах а, Ь, с, называется элементарной ячейкой кристалла.

Все элементарные ячейки, составляющие решетку, имеют одинаковую форму и объем. Во всех вершинах ячейки, называемых узлами, располагаются одинаковые атомы или группы атомов. Эти узлы эквивалентны друг другу. Для характеристики элементарной ячейки необходимо задать в общем случае шесть величин: периоды трансляций (а, Ь, с) и три угла между ними (а, Р, у). Эти шесть величин и определяют параметры элементарной ячейки.

Элементарные ячейки, содержащие частицы только в вершинах (узлах), называют простыми или примитивными. На каждую примитивную ячейку приходится только одна частица. Если элементарные ячейки содержат частицы не только в узлах, но и в других точках, то такие ячейки называют сложными.

Наиболее распространенными решетками являются простая кубическая, объемно-центрированная кубическая (ОЦК), гранецентрированная кубическая (ГЦК) (рис. 1.9). Можно показать, что ячейки 6 ив легко приводятся к простым, поэтому решетки с такими ячейками есть трансляционные решетки Бравэ.

Рис. 1.9. Простая кубическая решетка (а), ГЦК-решетка (б), ОЦК-решетка (в), двумерная решетка с базисом общего тина (г)

Решетка с Оазисом. На рис. 1.9, г показана двумерная решетка с базисом общего типа. Такую решетку можно представить в виде вставленных одна в другую двух решеток Бравэ 1 н 2, каждая из которых определяется одним трансляционным вектором а или Ь соответственно (на рис. 1.9, г узлы подрешетки 1 обозначены кружками, а узлы подрешетки 2 — крестиками). Смещение решеток 1 и 2 друг относительно друга описывается дополнительным вектором с, называемым базисным.

Индексы узлов. Положение любого узла решетки относительно выбранной системы координат ОХУ’А задается тремя его координатами х, у, г. Эти координаты кратны периодам трансляции х = та, у = пЬ, 2 = рс. Если за единицы измерений длин вдоль осей решетки принять параметры решетки а, Ь, с, то координатами любого узла будут числа т, п, р. Эти числа называются индексами Миллера узла и записываются в виде [[/и, п,р].

Для отрицательного индекса узла знак минус ставится над соответствующим числом. Например, для узла с координатами х = -2а;у = -Ь;г = Ъс индексы Миллера узла можно записать в виде [[2,1,3]].

Индексы направления. Для описания направления в кристалле выбирается прямая, проходящая через начало координат. Ее положение однозначно определяется индексами Миллера [[т, п, /у]] первого узла, через который данная прямая проходит. Поэтому индексы узла одновременно являются индексами направления, обозначаемыми в виде [т, п,р]. Таким образом, индексы Миллера направления представляют собой 3 наименьших целых числа, характеризующих положение ближайшего к началу координат узла, через который данное направление (прямая линия) проходит.

Индексы плоскости. Положение плоскости в кристаллографии определяется заданием трех отрезков А, В, С, которые она отсекает на осях решетки. Индексы Миллера такой плоскости определяются следующим образом. Выражают отрезки А, В, С в осевых единицах (периодах трансляции) и записывают величины, обратные этим отрезкам Полученные дроби приводят

к общему знаменателю И. Тогда целые числа, равные

являются индексами Миллера плоскости и записываются в виде (И к /).

Пример. Определить индексы Миллера плоскости, отсекающей на осях отрезки У соответствующих дробей общий знаменатель 0=2. Тогда у

плоскости индексы Миллера имеют вид: и записываются как (4 1 6).

Для кубического кристалла (периоды трансляции у которого одинаковы а = Ь = с) расстояние между соседними плоскостями данного семейства, характеризуемого индексами Миллера (Л к /), есть

На рис. 1.10 изображена решетка, базисом которой является шестигранная призма с основанием в виде правильного шестиугольника. Эта решетка характерна для кристаллов с гексагональной симметрией.

Рис. 1.10. Кристаллическая решетка гексагональной симметрии. Три базисные оси а₍, а₂, а₃ ориентированы друг к другу под углом 120°. Ось с перпендикулярна плоскости базиса (0 0 0 1)

Кристаллы с такой симметрией описываются в кристаллографии с помощью четырехосной системы координат. Три оси оц, а₂, а₃ лежат в плоскости базиса и ориентированы друг по отношению к другу под углом в 120°. Четвертая ось с перпендикулярна базисной плоскости. Все грани кристаллов гексагональной симметрии описываются четырьмя индексами Миллера (к к /’ /), где индексы к, к, / находят через длины отрезков, отсекаемых гранью кристалла от соответствующих базисных осей. Индекс / определяется через индексы к и к по формуле / = — <к+ к). Плоскость базиса, в которой лежат оси а_ь а₂, а₃, имеет индексы Миллера (() 0 0 1).

Видео:Металлическая кристаллическая решёткаСкачать

Кристаллическая решетка

1. КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА

Кристаллы характеризуются закономерным упорядоченным расположением частиц в пространстве, что соответствует минимуму внутренней энергии в условиях существования твердого тела. Анизотропия и симметрия физических свойств – характерная особенность кристаллов, обусловленная закономерностью и симметрией их внутреннего строения.

В кристаллическом многограннике и в вырезанной из него пластине наблюдается одинаково закономерное, симметричное, периодическое расположение частиц. Частицы, из которых сложены кристаллы, т. е. атомы, ионы, молекулы, образуют правильные симметричные ряды, сетки, решётки.

Каждому кристаллическому веществу присущи определенный порядок и симметрия в расположении частиц, четко установившиеся расстояния между частицами. Вследствие того, что в структуре кристалла в разных направлениях различны расстояния и силы связи между частицами, большинство свойств кристалла анизотропные, т. е. различны в разных направлениях, но одинаковы в направлениях, симметричных друг другу. Закономерность расположения частиц, их природа, их энергетический спектр и силы связи между ними определяют физические свойства кристалла. Внешние воздействия, такие как электрическое или магнитное поле, механическое воздействие или легирование

кристаллического тела чужеродными атомами, могут нарушать динамическое равновесие и менять свойства кристалла. Отсюда закономерность и симметрия структуры кристалла – следствие динамического равновесия многих сил и процессов. Таким образом, симметрия, периодичность и закономерность структуры – основные характеристики кристаллического состояния вещества.

Для каждой структуры характерен выбор её элементарных трансляций, или трансляционных групп, которые определяют пространственную решётку. Пространственная решётка является геометрической схемой, описывающей расположение материальных частиц в кристалле. Она строится на трех основных некомпланарных осях трансляции, или периодах решётки: a, b, c. В зависимости от отношения величин и взаимной ориентации трех основных трансляций a, b, c получаются решётки, отличающиеся друг от друга своей симметрией. Симметрия кристаллической структуры ограничивает число возможных решёток. Решётка должна быть инвариантной по отношению ко всем преобразованиям симметрии, возможным для данного кристаллического пространства. Основные трансляции, а значит, и решётка должны соответствовать симметрии структуры кристалла.

Точки пересечения, образующие пространственную решётку, называются узлами. Узел может находиться как в промежутке между материальными частицами, так и в центре тяжести одной частицы или группы частиц. Для металлических кристаллов узел совпадает с центром тяжести атома (иона).

Три элементарные трансляции определяют элементарную ячейку решётки,

или параллелепипед повторяемости. Исходя из идеи о периодическом расположении центров тяжести сферических материальных частиц в кристаллическом веществе, О. Бравэ в 1848г. показал, что всё многообразие кристаллических структур можно описать

с помощью 14 типов решёток, отличающихся по типам элементарных ячеек (рис.1) и по симметрии и подразделяющихся на 7 кристаллографических сингоний.

Решёткой Бравэ называется бесконечная система точек, которая образуется трансляционным повторением одной точки. Таким образом, каждая решётка Бравэ – это группа трансляций, характеризующих расположение материальных частиц в пространстве. В соответствии с решётками Бравэ кристаллы описываются 14 трансляционными группами. Решётки Бравэ играют исключительно важную роль в кристаллографии. Любую кристаллическую структуру можно представить с помощью одной из 14 решёток Бравэ.

Рис. 1. Типы элементарных ячеек

Для выбора элементарной ячейки Бравэ используют три условия:

1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла, т. е. наиболее высокой симметрии той сингонии, к которой относится кристалл; ребра элементарной ячейки должны быть трансляциями решетки.

2. Элементарная ячейка должна содержать максимально возможное число прямых углов или равных углов и равных ребер.

3. Элементарная ячейка должна иметь минимальный объём.

Эти условия должны выполняться последовательно, т. е. при выборе ячейки первое условие важнее второго, а второе важнее третьего. По характеру взаимного расположения основных трансляций или по расположению узлов все кристаллические решётки разбиваются, по Бравэ, на четыре типа (табл.1.)

Выбор примитивной ячейки, у которой узлы имеются только в вершинах, по условию Бравэ, даёт систему координат, которая является самой удобной для описания структуры и свойств кристалла. Примитивные ячейки Бравэ – это те основные ячейки, по которым были характеризованы сингонии кристалла. Требования выполнения условий выбора ячеек Бравэ предопределяет использование непримитивных (сложных) элементарных ячеек для описания некоторых кристаллических структур разных сингоний. К непримитивным (сложным) элементарным ячейкам относятся ячейки, которым принадлежит больше одного атома на каждую. В сложных ячейках имеются ещё узлы: в объемно-центрированной I ячейке – один узел в центре ячейки, в гранецентрированной F ячейке – по одному узлу в центре каждой грани, в базоцентрированной С (А, В) — ячейке – по одному узлу в центрах пары параллельных граней. Приняв один из узлов пространственной решётки за начало координат (за узел с символом [[000]]), можно найти все остальные узлы решётки с помощью трансляционной группы, т. е. совокупности основных трансляций элементарной ячейки (Rj ). У примитивных решёток достаточно определить три основные трансляции а, b, с, соответствующие рёбрам элементарной ячейки. Для всех остальных решёток нужно учитывать ещё дополнительные трансляции ρ j, соединяющие нулевой атом с неидентичными атомами, расположенными внутри элементарной ячейки или на её гранях.

Для того, чтобы выделить в структуре элементарную ячейку Бравэ, нужно, согласно правилам выбора элементарной ячейки, найти три кратчайшие некомпланарные трансляции а, b, с, которые обязательно должны соединять одинаковые узлы. Полученную элементарную ячейку необходимо проверить:

1. Можно ли на этих трансляциях построить ячейку, отвечающую правилам выбора ячейки Бравэ?

2. Все ли частицы в структуре можно получить с помощью такого выбора трансляций?

Согласно этим требованиям, элементарная ячейка описывается базисом. Базисом называется совокупность координат неидентичных атомов, входящих в элементарную ячейку. Атомы идентичны, если они химически одинаковы и структурно эквивалентны (т. е. их положение в структуре эквивалентно при заполнении бесконечного кристаллического пространства с помощью элементарной ячейки). Если атомы химически

неодинаковы или структурно неэквивалентны, они называются неидентичными. Например, в чистых кристаллических веществах, имеющих ОЦК решётку, в элементарной ячейке содержится два неидентичных атома, которые химически одинаковы, но имеют разное положение в структуре. Атомы одного типа располагаются в вершинах элементарной ячейки и принадлежат одновременно 8-ми ячейкам. Следовательно, на одну элементарную ячейку приходится 1 ⋅атом с 8 координатами [[000]]. Второй с координатами [[1/2 1/2 1/2 ]] находится в центре элементарной ячейки. Таким образом, базис ОЦК решётки чистого вещества записывается как [[000; 1/2 1/2 1/2 ]].

Если рассматривать расположение атомов NaCl, то атомы Na и Cl располагаются в плоскостях в шахматном порядке, причем в соседних плоскостях этого типа атомы натрия чередуются с атомами хлора. Обычно такое чередование атомов в решётке описывается элементом решётки, как показано на рис.2.

Рис. 2. Элемент решетки NaCl:

Однако этот элемент решётки NaCl не является элементарной ячейкой, поскольку его нельзя транслировать в пространстве. Для возможного транслирования в пространстве необходимо увеличить трансляции по осям Х, У, Z таким образом, чтобы с помощью полученной элементарной ячейки можно было описать все бесконечное пространство решётки NaCl: по осям Х, У и Z нужно удвоить расстояние между атомами, которые будут соединять между собой химически одинаковые атомы согласно закону их чередования в структуре. Эти расстояния и будут периодами кристаллической решётки NaCl, а элемент пространства – элементарной ячейкой NaCl, содержащей 8 ячеек (рис.1.10), в которой показано чередование атомов в трёхмерном пространстве и которую можно транслировать по осям координат (рис.3).

Рис.3. Элементарная ячейка решетки NaCl:

После определения базиса решётки становится возможным описание положения узлов, направлений и плоскостей в решётке. Любой узел решётки определяется радиус-вектором R =ma+nb + рс, соединяющим выбранный за нулевой узел с данным узлом.

Совокупность чисел m, n, р, записанная в двойных квадратных скобках [[mnр]], называется символом узла, а три числа m, n, р – индексами узла. Числа в символе пишутся подряд, без запятых, читаются порознь. Знак минус пишется над цифрой. Ряд или узловая прямая в решётке, а также ребро кристаллического многогранника характеризуются наклоном в выбранной системе координат. Если ряд не проходит через начало координат, он проводится параллельно самому себе через начало координат.

В виду этого все параллельные направления в кристалле равнозначны и обозначаются как [UVW], где U, V, W – проекции на оси координат атома, ближайшего к «нулевому» в ряду [UVW], проходящему через «нулевой» атом. Все направления данного семейства обозначаются . Если индексы в символе ряда кратные, их необходимо сокращать на целое положительное число.

Любая грань кристалла или плоскость, проведенная через узлы пространственной решётки, параллельна какой-либо плоской сетке, а значит бесконечному числу плоских сеток. Если плоскость решётки пересекает все три оси координат, отсекая на них отрезки ma, nb, pc, то отношение чисел m:n:p характеризует наклон плоскости к осям координат. Этим отношением определяется и ориентировка всего семейства параллельных ей плоскостей.

Серию отношений рациональных чисел m:n:p для всех параллельных плоскостей можно представить как отношение целых взаимно простых чисел p:q:r, которые называются параметрами Вейсса. Например, если параллельные плоскости отсекают на осях координат отрезки: 1-я плоскость — а b∞, 2-я плоскость а2b∞ и т. д., то полученные соотношения будут 1 :1 : ∞ = 1: 2 : ∞

В кристаллографии принято характеризовать плоскости или нормали к ним не параметрами, а индексами Миллера. Индексы Миллера – это величины, обратные параметрам Вейсса, приведённые к целым числам. Если параметры плоскости p, q,r (отрезки, отсекаемые плоскостью по осям координат), то индексы Миллера определяются из соотношения:

1 : 1 : 1 = h: k : l. (1.1)

В приведённом примере h : k : l =1 : 1 : 1 = 1 : 1 :1/∞ = 2 : 3 : 0.

Числа h, k,l называются индексами плоскости; индексы, написанные подряд и заключённые в круглые скобки (hkl), называются символом плоскости. Символом (hkl) характеризуется вся совокупность параллельных плоскостей. Этот символ означает, что система параллельных плоскостей рассекает отрезок а на h частей, отрезок в на k частей и отрезок с на l частей, т. е. величины h, k,l обратно пропорциональны отрезкам, отсекаемым этой плоскостью на осях координат. Все плоскости данного семейства обозначаются фигурными скобками: . Если индексы в символе ряда кратные, их

необходимо сокращать на целое положительное число (рис.4).

Символы осей координат не зависят от углов между осями координат и от осевых отрезков, они одинаковы в любой системе координат. В общем виде уравнение плоскости записывается как

где N – всегда целое число;

h, k,l – взаимно простые, целые числа.

Для плоскости, проходящей через начало координат, N = 0, для плоскости, ближайшей к началу координат, N=1.

Каждое семейство направлений и плоскостей , в котором все индексы имеют разные значения, содержит 48 разных вариантов [uvw] или (hkl), тогда как в семействах и − их 24, в семействах и – 8, в и –12, в семействах и – 6.

Следует отметить, что прежде чем характеризовать положение узлов, индексы направлений и плоскостей в решётке, необходимо сначала выбрать элементарную ячейку и описать её базис. От координат атомов базиса и выбора периодов элементарной ячейки зависят индексы узлов, направлений и плоскостей в решётке. Например, фаза имеет примитивную кубическую решётку состава АВ, в которой атомы компонентов А и В хаотично занимают узлы решётки. В этом случае элементарной ячейкой фазы является куб с периодом а, описываемый положением нулевого атома.

В геометрической кристаллографии в физическом металловедении обычно не рассматривается внешняя форма, размеры граней и самих кристаллов, так как, например, внешняя форма и размеры кристаллов зависят прежде всего от внешних условий, в которых кристалл образовался. Главная задача кристаллографии в физическом металловедении – точно отобразить углы между плоскостями. Существует закон постоянства углов: для всех кристаллов одного и того же вещества в одной и той же модификации углы между соответствующими плоскостями одинаковы.

Цель кристаллографических проекций: удобно и точно изобразить и измерять на плоском листе бумаги угловые соотношение между плоскостями, направлениями и элементами их симметрии. С помощью кристаллографических проекций исследуют в металловедении линии скольжения, двойники, выделения новых фаз, ориентировку монокристаллов, преимущественную ориентировку зерен в поликристаллах и целый ряд других задач.

Кристаллографический и полярный комплексы

В кристаллографии проектируется не кристалл, а кристаллографический комплекс, полученный от данного кристалла.

Кристаллографический комплекс получается при параллельном перемещении плоскостей в пространстве до взаимного пересечения их в одной точке. В некоторых случаях проектируется полярный комплекс, который обратен кристаллическому (рис.3.2). Полярный комплекс получается при восстановлении из центра кристаллографического комплекса перпендикуляров ко всем плоскостям. Таким образом, в полярном комплексе плоскость заменяется её нормалью.

Для упрощения рассмотрения кристаллографических задач — плоскости или нормали к ним проектируют на различные поверхности (плоскость, сферу), что приводит к различным кристаллографическим проекциям.

В кристаллографии чаще других рассматриваются следующие проекции:

1) сферическая; 2) гномосферическая;

3) стереографическая; 4) гномостереографическая, 5 ) гномоническая;

Сферическая и гномосферическая проекции.

Вокруг центра кристаллографического комплекса произвольным радиусом описывается сфера, которая называется сферой проекции. Плоскости кристалла пересекают сферу по кругам наибольшего диаметра, т. е. по большим кругам. Если все плоскости проектировать подобным образом на сферу, то большие круги пересекутся под тем же углам, что и плоскости кристалла (рис.).

Если в центр сферы проекций поместить полярный комплекс, то получится гномосферическая проекция, в которой кристаллографическая плоскость отображается полюсом Р – точкой пересечения перпендикуляра к плоскости с поверхностью сферы (рис.). Совокупность полюсов на сфере называется полюсной фигурой. По размещению полюсов на сфере, образующих полюсную фигуру, можно определить ориентировку кристаллографических плоскостей, т. к. угол между двумя плоскостями в кристалле равен углу между их полюсами.

Стереографическая и гномостереографическая проекции.

Практически более удобно пользоваться не сферой проекций, а её плоским изображением, т. к. как при этом вся работа может быть выполнена на листе бумаги. Необходимо спроектировать сферу без нарушения углов между плоскостями или полюсами. Углы на сфере проектируются на стереографическую проекцию без искажений. Для этого источник света S (или центр проекции) необходимо поместить в какой-либо точке, лежащей на поверхности сферы, а плоскость проекции расположить перпендикулярно к диаметру, проходящему через центр сферы и центр проекции. Расстояние плоскости от поверхности сферы не имеет значения, так как, при изменении расстояния меняется только увеличение изображения, но не угловые соотношения.

Возможно отобразить всю сферу в пределах основного круга при совмещении двух проекций и различать их знаками + и −. Любая плоскость, проходящая через точки NS, рассечёт сферу по большому кругу, который спроектируется на плоскость проекции в виде прямой линии. Любой большой круг, проходящий через точку N, проектируется на плоскость в виде прямой линии. Отображающий диаметр основного круга проекций (круг SN – горизонтально проектируется в ЕЕ). Большой круг – это окружность на поверхности сферы, радиус которой равен радиусу сферы. Если большой горизонтальный круг разделить на градусы, то его проекция ЕЕ′ будет служить шкалой для стереографически спроектированных точек, лежащих на горизонтальном круге. Так же наносятся деления на вертикальный круг ML, которые проектируются на основной круг.

По экватору измеряется угол ρ в пределах 0-1800, по основному кругу меридиану — угол ϕ в диапазоне 0-3600 по часовой стрелке. Таким образом, можно спроектировать на плоскость глобус с линиями широты и долготы (меридианами и параллелями). Если ось, проходящую через северный и южный полюсы, спроектировать перпендикулярно к плоскости проекции, то стереографическая проекция всех параллелей и меридианов образует сетку Болдырева (рис. 3.9). Если ось, проходящая через северный и южный полюсы сферы, параллельна плоскости проекции, то линии долготы и широты образуют стереографическую сетку, называемую сеткой Вульфа. Важно отметить, что углы между пересекающимися плоскостями сохраняются неизменными в стереографической проекции и легко поддаются измерению. Исходя из таких предпосылок, формируются свойства стереографической и гномостереографической проекций.

Стереографическая проекция полюсов всех важнейших плоскостей и направлений кристалла с малыми индексами называется стандартной проекцией. Ясно, что стандартная проекция (стандартная сетка) кубического кристалла может рассматриваться и как стереографическая проекция (тогда в точки-полюсы проектируются кристаллографические направления), и как гномостереографическая проекция (тогда кристаллографические плоскости отображаются полюсами на сетке).

Если оси Х и У кристалла лежат на плоскости проекции, то полюсы плоскостей (100) и (010) расположены на основном круге (рис.). Ось Z перпендикулярна к плоскости проекции, поэтому полюс плоскости (001) находится в центре этого круга.

Изображение производится путем откладывания углов между полюсами и кристаллографическими осями с помощью стереографической сетки.

Процесс построения значительно сокращается при использовании:

1) свойства симметрии кристалла;

2) зональных соотношений – определении полюсов посредством пересечений кругов зон.

Стандартные кристаллографические проекции для кристаллов кубической системы одинаковы для всех кристаллических веществ с кубической решёткой. Это объясняется тем, что уравнение, описывающее связь углов между плоскостями и индексами плоскостей в кубической решётке не содержит значений периодов решётки и координатных углов:

В кубических решётках всех типов (примитивной кубической ПК, объемно-центрированной ОЦК, гранецентрированной ГЦК) с любыми периодами углы между плоскостями одинаковы и одинаковы кристаллографические проекции для любых веществ с кубической решёткой.

В кристаллах более низкой симметрии, чем кубическая, углы между плоскостями зависят от соотношений периодов решётки и координатных углов. Например, в тетрагональной решётке

Следовательно, для кристаллов средних и низших сингоний кристаллографические проекции строятся для конкретных соотношений периодов и координатных углов.

Свойства стереографической и гномостереографической проекций

1. На стереографической проекции кристаллографическая плоскость, совпадающая с большим кругом, параллельным плоскости проекции, изображается основным кругом.

2. Кристаллографические плоскости, совпадающие с большим кругом, перпендикулярным плоскости проекции, проектируются в виде диаметра основного круга.

3. Наклонные плоскости изображаются в виде проекций наклонных больших кругов, которые при повороте сетки Вульфа могут совпадать с одним из меридианов.

4. Кристаллографические направления на стереографической проекции изображаются в виде точек (полюсов). Поэтому стереографическая проекция плоскостей, принадлежащих одной зоне, изображаются в виде проекции кругов, пересекающихся в одной точке.

5. Гномостереографическая проекция есть проекция обратной решетки. Кристаллографические плоскости на гномостереографической проекции изображаются в виде полюсов, а кристаллографические направления в виде проекции больших кругов. Поэтому на гномостереографической проекции полюса плоскостей, принадлежащих одной зоне, лежат на проекции одного круга, который при вращении сетки можно совместить с одним из меридианов.

6. Для кристаллов кубической сингонии можно пользоваться одними и теми же стандартными проекциями при изображении кристалла в стерео — или гномостереографической проекциях. Это связано с тем, что в кубической сингонии плоскости и перпендикулярные к ним направления имеют одни и те же индексы, а углы между пересекающимися плоскостями равны углам между нормалями к соответствующим плоскостям.

7. Углы между двумя точками на проекции не изменяются при вращении точек вокруг оси (центра) стереографической проекции.

8. Угол между двумя полюсами на проекции равен разности их широт, угол между двумя точками равен разности их долгот, когда они лежат на экваторе (горизонтальном диаметре). Для измерения угла между двумя полюсами необходимо, поворотом сетки Вульфа вокруг её центра, совместить их с экватором или меридианом, которые служат шкалой для отсчёта угловых градусов.

Построение гномостереографических проекций

Для построения гномостереографических проекций важно то, что плоскость, индексы которой (h3k3l3) равны сумме одноименных индексов двух плоскостей зоны [UVW], принадлежит той же зоне [UVW]:

На гномостереографической проекции полюса плоскостей, принадлежащие зоне, располагаются на угловом расстоянии 90о от проекции, изображающей ось зоны, и находятся на одном меридиане сетки Вульфа, если проекция оси зоны располагается на экваторе. При этом угол между полюсами плоскостей, лежащих на меридиане, является углом между этими плоскостями. В случае если заданы две плоскости и нужно найти их зону и её ось, следует концентрическим поворотом кальки установить проекции плоскостей на меридиан и от точки его пересечения с экватором отсчитать 90о к центру проекций. Полученная на экваторе точка и будет проекцией оси зоны, так как отстоит на 90о от любой из точек меридиана (рис.). Проекция плоскости (hkl), принадлежащая двум зонам, на сетке Вульфа является точкой пересечения двух меридианов, на которых расположены проекции плоскостей, образующих эти зоны.

При построении стандартных проекций с помощью закона зон достаточно в качестве исходных данных знать положение четырёх непараллельных друг к другу плоскостей кристалла (трех координатных и единичной (111)). Это положение определяется величинами углов между плоскостями (001) и (111), (100) и (111), (010) и (111), которые рассчитываются по формуле, устанавливающей значение косинуса угла между плоскостями в зависимости от значений индексов плоскостей по формулам для решётки кристаллов соответствующих сингоний.

Гномостереографическая проекция кристаллов строится на сетке Вульфа. Поскольку каждая плоскость кристалла принадлежит, по крайней мере, двум зонам, то положение плоскости определяется точкой пересечения зон. Четыре исходные плоскости (001), (010), (100) и (111) принадлежат шести зонам индексы которых находятся по формуле для расчёта оси зоны: [100], [010], [001], [111],[101],[011]. В качестве оси проекции выбирается перпендикуляр к плоскости (001) прямой кристаллической решётки. Проведя эти шесть зон как соответствующие меридианы, в точках их пересечения находят новые плоскости, индексы которых вновь определяются по закону зон: на пересечении зон [100] и [011] расположена плоскость (011) , на пересечении зон [101] и [010] – плоскость (101), на пересечении зон [001] и [110]- плоскость (110).

Следует отметить, что для кристаллических решёток, имеющих симметрию более низкую, чем кубическая, в качестве исходных плоскостей для построения гномостереографической проекции лучше выбрать шесть плоскостей (001), (010), (100), (110), (101), (011), так как положение соответствующих полюсов легче найти на плоскости проекции. Углы между ними рассчитываются по формуле косинуса угла между плоскостями для решётки данной сингонии, и положение полюсов данных плоскостей обозначаются на проекции. В центре проекции, как и в первом случае, устанавливается полюс (001), который является перпендикуляром к плоскости (001) для решётки данной сингонии. Далее проводятся меридианы через полюса (100) и (011), (001) и (110), (010) и (101) и находится точка их пересечения, которая является полюсом (111) и вершиной сферического треугольника (рис.). Затем операции продолжают, приняв во внимание новые зоны и точки их пересечения.

Построение следует вести в сферическом треугольнике, ограниченном проекциями плоскостей (001) – (100) – (010). После разделения сферического треугольника (001) – (100) – (010) на три области, ограниченные проекциями (полюсами) плоскостей,

находят их вершины, которые получаются на пересечении зон с осями: первая — [110] и [111], вторая [101] и [111], третья [011] и [111] (рис.4.3). Индексы проекций плоскостей, находящихся на пересечении зон в вершинах сферических треугольников, рассчитывают по правилу зон или сложением одноимённых индексов плоскостей, лежащих в их основании и принадлежащих одной зоне:

(001) + (111) = (112) или (101) + (011) = (112);

(100) + (111) = (211) или (101) + (110) = (211);

(110) + (011) = (121) или (111) + (010) = (121).

Затем деление сферических треугольников продолжают, получив новые зоны и точки их пересечения, которые являются вершинами новых сферических треугольников и полюсами плоскостей.

Гномостереографическая проекция строится в пределах сферического треугольника, ограниченного полюсами (100)-(010)-(001), а положения полученных полюсов плоскостей внутри него симметрично переносятся в соответственные положения других секторов проекции. Достаточно осуществить построение одной стереографической проекции кристаллической решётки сечением (001), получение других сечений решётки данного типа осуществляется поворотом таким образом, чтобы интересующая ось проекций вышла в центр проекции. При этом следует помнить, что на гномостереографических проекциях для кристаллических решёток некубических сингонии ось проекций является нормалью к соответствующей плоскости, а не направлением в кристалле.

Для того чтобы получить гномостереографические проекции направлений кристаллов более низких сингоний, чем кубическая, нужно “перейти в обратное пространство”, т. е. по формулам обратной решётки для кристаллов анализируемой сингонии найти её периоды а*, в*, с*, симметрия же обратной решётки сохраняется такой же, как у прямой кристаллической. В обратной решётке, как было показано выше, нормали к плоскостям обратной решётки являются направлениями прямой кристаллической решётки с соответствующими индексами. Построение гномостереографических проекций производится аналогичным образом. Как правило, ограничиваются построением гномостереографической проекции [001], отображающей направление в кристалле.

На построенных гномостереографических проекциях углы между полюсами являются истинными углами между плоскостями на проекции плоскостей и углами между направлениями на проекции направлений. Построенные гномостереографические проекции для плоскостей и направлений накладываются друг на друга таким образом, чтобы осуществлялось точное совмещение полюсов одноименных плоскостей и направлений и/или между ними выполнялся точный угол разориентировки. Проще всего осуществить совмещение сечений (001) прямой и (001)* обратной решёток, поскольку для решёток всех сингоний, кроме триклинной, нормаль к плоскости (001) совпадает с направлением [001] в кристалле. Как правило, вторым полюсом для проведения совмещения проекций выбирается полюс (100) на проекциях плоскостей и направлений.

Полученная объединенная гномостереографическая поверхность плоскостей и направлений, на которой обозначены положения полюсов как плоскостей, так и направлений в кристалле, очень удобна для анализа структур кристаллов, имеющих решётки не кубической сингонии, особенно для кристаллов с тетрагональной и гексагональной решётками.

При определении взаимной ориентации кристаллов, когда на микродифракционной картине наблюдается много рефлексов, полученных от кристаллов разных ориентировок, правильность расшифровки электронограммы можно проверить, построив теоретические дифракционные картины, соответствующие рассчитанным. Найдя на объединённой гномостереографической проекции плоскостей и направлений кристалла анализируемой сингонии нужную ось зоны, т. е. полюс направления, проекцию поворачивают таким образом, чтобы этот полюс находился в центре проекции, а полюса плоскостей располагались на большом круге проекций (рис.). Соединив прямыми линиями, проходящими через центр круга проекции, положение полюса оси зоны, полюсы плоскостей с одноимёнными индексами, получаем сечение электронограммы, на котором показаны углы между плоскостями для данной зоны, так как полюсы плоскостей являются

точками пересечения перпендикуляров к плоскостям со сферой проекций.

Определение угла между двумя направлениями.

Поскольку все направления и плоскости кристаллографического комплекса проходят через общую точку – центр комплекса, то любые два направления комплекса всегда лежат в одной плоскости. Угол между двумя рассматриваемыми направлениями находится в этой же плоскости, которая на стереографической проекции изображается меридианом. Поэтому кальку с нанесенными на ней точками, являющимися проекциями рассматриваемых направлений, поворачивают вокруг центра сетки Вульфа до тех пор, пока эти точки (1–2) не окажутся на одном меридиане сетки (рис.). Искомый угол α определяют по разности широт, определяемым параллелями точек 1, 2. Если проекции двух направлений получены проектированием из разных полусфер (на кальке отмечены соответственно точка 3′ и крестик 4), то кальку поворачивают таким образом, чтобы оба выхода направлений попали на симметричные меридианы относительно нулевого меридиана. Искомый угол α определяется суммой углов α1 и α2, отсчитываемых по соответствующим меридианам до полюса сетки.

Возможен и другой вариант нахождения угла α. Для этого следует перевести проекцию направления 4 (крестик) в точку 4′, что будет отвечать случаю проектирования обоих рассматриваемых направлений из одной (северной) полусферы. Перевод крестика 4 в точку 4′ осуществляется просто: крестик 4 соединяют прямой с

центром проекции, на продолжении этой прямой откладывают расстояние, равное расстоянию от крестика до центра. Полученную точку 4′ располагаем на одном меридиане с точкой 3′. Искомый угол α’ = 180° – α отсчитывают вдоль этого меридиана.

Определение направляющих углов для направления.

Направляющие углы α, β, γ для произвольного направления можно определить после последовательного измерения углов между стереографической проекцией этого направления R и стереографическими проекциями осей системы координат x, y, z (рис.).

Если известны направляющие углы α, β, γ для направления, то координаты Rx и Ry стереографической проекции этого направления вычисляют как

Процедура определения сферических углов φ и θ для произвольной прямой показана на рис., а координаты Rx и Ry стереографической проекции этой прямой вычисляют как

Определение угла между двумя плоскостями.

Поскольку угол между плоскостями равен углу между нормалями к этим плоско-

стям, то достаточно определить угол между гномостереографическими проекциями плоскостей. Сначала найдем нормали N1 и N2 к плоскостям P1 и P2 (рис), затем, поворачивая кальку, добиваемся совмещения точек N1 и N2 с одним из меридианов сетки Вульфа. Искомый угол α определяется вдоль этого меридиана.

Симметрия кристаллического пространства определяется заданием всех преобразований, которые сохраняют расстояния между любыми точками пространства и приводят к совмещению пространства с самим собой. Элементы симметрии делят на закрытые и открытые. Открытые элементы симметрии содержат трансляции и поэтому описывают симметрию бесконечного пространства. Закрытые элементы симметрии оставляют одну точку неподвижной и после конечного числа операций возвращают кристаллическое пространство в исходное положение. Закрытые элементы симметрии задаются матрицами ортогонального преобразования R с detR = ± 1. Они могут быть сведены к поворотным осям симметрии (чистое или собственное вращение с detR = + 1) и к инверсионным осям (вращение с отражением в точке, лежащей на оси, или несобственное вращение с detR = − 1).

Поворотные оси симметрии

Осью симметрии называют прямую, при повороте вокруг которой на некоторый угол αn гомологические (эквивалентные) точки кристаллического пространства совмещаются. Угол поворота αn равен 360о/n, где n − целое число. Значит, через n поворотов в одном направлении на угол αn кристаллическое пространство возвращается в исходное положение. Наименьший угол поворота αn для данной оси симметрии называют элементарным углом оси симметрии, а n − порядком оси поворота. В кристаллографической системе координат при повороте вокруг оси симметрии произвольный вектор x, задающий узел пространственной решетки, переходит в вектор x′:

где R − матрица вращения, а x и x′ − векторы-столбцы.

В ортогональной системе координат преобразование R будет описываться матрицей подобия R′ = CRC-1, где C − матрица перехода от кристаллографической системы координат к ортогональной системе. Если ортогональную систему координат выбрать таким образом, чтобы ось симметрии совпала с осью x, то поворот вокруг этой оси будет описываться матрицей R′ вида

След этой матрицы trR′ = trR = N = 1 + 2 cosα; N может принимать значения 0, ±1, +2, +3. Отсюда следует, что возможны лишь повороты на угол α, равный 0, 60, 90, 120 и 180° (табл. 1.2). Таким образом, в кристаллическом пространстве возможны оси симметрии первого, шестого, четвертого, третьего и второго порядков.

💡 Видео

Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Типы кристаллических решеток. 8 класс.Скачать

Векторы #3: многомерные системы координат, базисные векторыСкачать

Разложение вектора по базису. 9 класс.Скачать

Кристаллография. Лекция 21. Решетки Браве, часть 1Скачать

9. Кристаллические решетки.Скачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Урок 420. Дифракция света. Дифракционная решеткаСкачать

Вещества с атомной кристаллической решеткой за 1 минуту!Скачать

1.1 Симметрия кристаллов: элементы симметрии, пространственная решётка и базис.Скачать

Кристаллические решетки | Химия ЦТ, ЕГЭСкачать