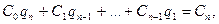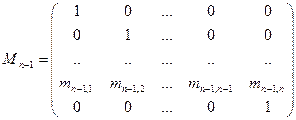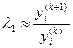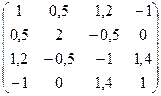- Отыскание собственных значений матрицы
- Задания лабораторной работы №3
- Методы решения задач о собственных значениях и векторах матриц
- Постановка задачи
- Метод непосредственного развертывания
- Алгоритм метода непосредственного развертывания
- Метод итераций для нахождения собственных значений и векторов
- Алгоритм метода итераций
- Метод вращений для нахождения собственных значений
- Алгоритм метода вращений
- 🔍 Видео
Видео:Собственные векторы и собственные значения матрицыСкачать

Отыскание собственных значений матрицы
Академик А.Н.Крылов в 1931 году одним из первых предложил довольно удобный метод раскрытия определителя (2).
Суть метода А.Н.Крылова состоит в преобразовании определителя D() к виду
Равенство нулю определителя D() есть необходимое и достаточное условие для того, чтобы однородная система линейных алгебраических уравнений
имела решение х1, х2, …, хn, отличное от нулевого.
Преобразуем систему (2) следующим образом. Умножим первое уравнение на и заменим x1, …,xn их выражениями (2) через x1,…, xn.
Умножим далее уравнение (3) на и заменим снова x1, …,xn их выражениями через x1,…, xn. Получим
Повторяя этот процесс (n-1) раз, мы перейдем от системы (2) к системе
коэффициенты которой будут определятся по рекуррентным формулам
Очевидно, что определитель системы (5) будет иметь вид (1).
Система линейных алгебраических уравнений (5) имеет ненулевое решение для всех значений , удовлетворяющих уравнению D()=0. Таким образом, D1()=0 при всех , удовлетворяющих уравнению D()=0.
Пусть все корни D() различны. Так как все корни D() являются корнями D1(), то D1() делится на D(). Так как, кроме того, степени D1() и D() одинаковы, то частное должно быть постоянным. Сравнивая коэффициенты при n, получим
В случае, если D() имеет кратные корни, равенство (8) сохраняется.
Рассмотрим теперь коэффициенты bik, определяющие D1(). Введем в рассмотрение векторы Bi с компонентами bi1, bi2, …, bin. Равенства
показывают, что Bi=ABi-1, где A — матрица, транспонированная к данной. Из этого следует, что
Bi=A i-1B1, B1=AB0, (9)
Если С0, то уравнения D1()=0 и D()=0 эквивалентны. Если же С=0, то это преобразование ничего не дает. А.Н.Крылов предлагает в этом случае особый прием, рассмотренный ниже. Возьмем в качестве вектора В0 произвольный вектор В0=(bi1,bi2,…,bin) и получим с его помощью по формулам (9) векторы Вi.
Пусть u=b01x1+b02x2+…+b0nxn (10)
где x1,x2,…xn — решения системы (1/). Тогда повторяя прежние рассуждения, получим:
Решая эту систему как систему линейных однородных уравнений с n+1 неизвестными u,x1,x2,…xn, получим, что ненулевое решение возможно в том и только в том случае, когда
Повторяя прежние рассуждения, найдем, что
если С10, то коэффициенты рi характеристического многочлена определяются как отношения где Di — алгебраические дополнения элементов n-i в определителе D().
Но сущность метода Крылова и состоит в том, чтобы находить эти коэффициенты, не подсчитывая миноры.
Воспользуемся теоремой Гамильтона — Кэли о том, что матрица является корнем своего характеристического уравнения, т.е.
где рi — коэффициенты характеристического многочлена.
Умножая равенство (14) на b0, получим:
Это векторное равенство дает систему линейных алгебраических уравнений для определения коэффициентов характеристического многочлена. Определитель этой системы равен С1. Решать полученную систему можно любым из известных методов, например, методом Гаусса.
Можно было бы применить теорему Гамильтона — Кэли и для самой матрицы А, получили бы тогда систему
здесь ci=Aic0, c0
— произвольный начальный вектор.
Пример. Пусть матрица A имеет вид:
в качестве вектора В0 возьмем вектор В0=(1,0,0,0). Тогда получим векторы
В1=АВ0, В2=А2В0= АВ1, В3=А3В0=АВ2, В4=А4В0=АВ3:
Система линейных алгебраических уравнений для определения коэффициентов характеристического многочлена имеет вид:
Решив эту систему, получим: р1=-11, р2=7, р3=72, р4=-93. Поэтому характеристический многочлен примет вид:
D()= 4 -113 + 72 +72 -93.
В приведенном примере С10.
В случае, если С=0, такая система не даст возможности определить коэффициенты характеристического уравнения. Матрица А и транспонированная к ней матрица А удовлетворяет своему характеристическому уравнению D(A)=0. Но может оказаться, что существуют многочлены () степени меньше n, для которых также выполняется равенство (А)=(А)=0. Среди таких многочленов имеется единственный многочлен со старшим коэффициентом 1, имеющим наименьшую степень. Этот многочлен называется минимальным. Если минимальный многочлен матрицы не совпадает с характеристическим, то С=0 при любом выборе начального вектора. В этом случае АС0=0 и векторы С0, АС0, …,Аn-1C0 линейно зависимы.
На практике при использовании метода Крылова такая ситуация может возникнуть лишь при особых обстоятельствах.
Можно подсчитать, что при раскрытии характеристического многочлена матрицы с помощью метода Крылова потребуется 0,5(2п3+п2+п) операций умножения и деления.
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Задания лабораторной работы №3
Лабораторная работа №3
«Нахождение собственных чисел и собственных векторов матрицы»
1. Метод Крылова. Собственные числа матрицы А определяют путём решения характеристического уравнения, приведённого к виду
Значение 
где 


Собственные векторы матрицы А определяют из соотношения

где 

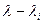
Пример решения задачи методом Крылова
A =
1. Для определения коэффициентов характеристического уравнения
строим последовательность векторов:
Если векторы В0, В1, В2, В3 окажутся линейно независимыми, то коэффициенты p1, p2, p3, p4 определяются из решения системы линейных уравнений, соответствующей равенству
Систему линейных уравнений решаем средствами Excel или MathCAD, можно воспользоваться также программной реализацией метода Гаусса из лабораторной работы №1.
| А | В0 | В1 | В2 | В3 | В4 | |
| 2,2 | 0,5 | 2,2 | 10,09 | 52,373 | 291,0006 | |
| 1,3 | 6,5 | 41,84 | 239,605 | |||
| 0,5 | 0,5 | 1,6 | 0,5 | 6,55 | 37,64 | 220,7825 |
| 1,6 | 10,20 | 57,56 | 321,930 |
Таким образом, характеристическое уравнение матрицы имеет вид

2. Определение собственных чисел матрицы состоит в решении полученного характеристического уравнения (*), например, средствами Excel или MathCAD, можно использовать программную реализацию одного из методов лабораторной работы №2.
Собственные числа матрицы А таковы:
3. Собственный вектор Xi, соответствующий собственному числу li , определяется по формуле
где коэффициенты при ранее найденных векторах В0, В1, В2, В3 находятся из равенства

Окончательные значения собственных векторов должны иметь кубическую норму, равную единице. Для того, чтобы собственный вектор имел кубическую норму, равную единице, нужно разделить все компоненты вектора на максимальную по модулю компоненту.
Все вычисления приведены в таблице 2.
| li | bi3B0 | bi2B1 | bi1B2 | bi0B3 | Xi |  |
| 5,652 | 0,4877 | –4,7672 –2,1669 –1,0334 –4,3338 | –3,5113 –2,2620 –2,2794 –3,5496 | 52,373 41,84 37,64 57,56 | 44,5822 37,4111 34,2772 49,6766 | 0,879 0,753 0,690 1,0 |
| 1,545 | 1,7918 | –15,5826 –7,08298 –3,5415 –14,1660 | –44,9510 –28,9575 –29,1802 –45,4410 | 52,373 41,84 37,64 57,56 | –6,3688 5,7995 4,9183 –2,0470 | –0,911 –0,772 0,321 |
| –1,420 | –1,9427 | 22,7400 10,3364 5,1682 20,6728 | –74,8678 –48,2300 –48,6010 –75,6840 | 52,373 41,84 37,64 57,56 | –1,6975 3,9464 –5,7928 2,5488 | 0,293 –0,681 –0,440 |
| 0,2226 | 12,4042 | –5,2692 –1,4860 –0,7430 –2,9720 | –58,2940 –37,5531 –37,8420 –58,9295 | 52,373 41,84 37,64 57,56 | 3,2140 2,8009 –0,9450 –4,3415 | –0,740 –0,645 –0,218 |
2. Метод Данилевского. Для определения коэффициентов характеристического уравнения матрицу A с помощью n-1 преобразований подобия заменяют подобной ей матрицей Фробениуса
P=
На первом этапе находят:
где
где

где
Пример решения задачи методом Данилевского
A =
1. Коэффициенты характеристического уравнения матрицы А определяются как элементы первой строки матрицы Фробениуса Р, подобной данной матрице А. Матрицу Р найдем в результате трех преобразований подобия:
Округляя значения коэффициентов до четырех десятичных знаков, получим характеристическое уравнение
l 4 – 6l 3 – 0,2l 2 + 12,735l – 2,7616 = 0.
Это уравнение решаем средствами Excel или MathCAD, можно использовать программную реализацию одного из методов лабораторной работы №2. Корни уравнения таковы:
2. Собственный вектор Xi , соответствующий собственному числу li , определяется равенством
Xi = М3 ×М2× М1×Yi, где Yi = 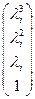
Результаты вычисления собственных векторов приведены в таблице 3.
| li | M1 | M2 | M3 | Yi | Xi |  |
| 5,652 | –0,231125 1,078582 1,651001 1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 180,5537 31,9451 5,652 | 0,8977 0,7529 0,6898 | 0,898 0,753 0,690 |
| 1,545 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 3,6880 2,3870 1,545 | 3,1143 –2,8359 –2,4048 | –0,911 –0,772 –0,440 |
| 0,2226 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 0,01103 0,4955 0,2226 | –0,7403 –0,6451 0,2177 | –0,740 –0,645 0,218 |
| –1,420 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | –2,8633 2,0164 –1,420 | –0,6665 1,5480 –2,2719 | 0,293 –0,681 –0,440 |
3. Метод итераций для определения первого собственного значения и соответствующего ему собственного вектора матрицы А. Строят последовательность векторов: 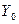

где 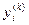

При этом собственный вектор 
Пример решения задачи методом итераций
1. Строим последовательность векторов 


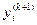

Все вычисления приведены в таблице 4.
Таблица 4
| 1,6 | 2,3 | 1,2 | ||||
| A | 2,3 | 0,6 | 1,5 |  |  |  |
| 1,2 | 1,5 | 3,8 | ||||
 | ||||||
 | 5,1 | 4,4 | 6,5 | 5,11 | 5,48 | 5,76 |
 | 26,08 | 24,12 | 37,42 | 5,45 | 5,41 | 5,60 |
 | 142,108 | 130,586 | 209,672 | 5,484 | 5,511 | 5,548 |
 |  |  |  | 5,5151 | 5,5148 | 5,5321 |
 |  |  |  | 5,5205 | 5,5225 | 5,5267 |
 |  |  | 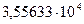 | 5,5233 | 5,5235 | 5,5251 |
 |  |  |  | 5,5240 | 5,5241 | 5,5246 |
 | 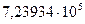 |  |  | 5,5242 | 5,5243 | 5,5244 |
 | 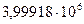 |  |  | 5,5243 | 5,5243 | 5,5244 |
 |  |  |  | 5,5243 | 5,5243 | 5,5243 |
 |  |  |  |
Итак, 
2. Собственный вектор 





Задания лабораторной работы №3
«Нахождение собственных чисел и собственных векторов матрицы»
Задание для нечетных вариантов:
1. Используя метод Крылова найти собственные числа и собственные вектора матрицы А. Разрешается реализовывать метод Крылова средствами MathCAD или Mathematica (корни характеристического уравнения найти с помощью встроенных функций). Метод Крылова можно реализовать также на VBA (корни характеристического уравнения найти с помощью команды «Поиск решения» или «Подбор параметра» пункта меню Сервис в Excel).
2. Используя метод итераций, определить первое собственное число матрицы (наибольшее по модулю). Найти соответствующий ему собственный вектор, имеющий кубическую норму, равную 1. Метод итераций реализовать на языке программирования.
3. Сравнить результаты, полученные методом Крылова и методом итераций.
Задание для четных вариантов:
1. Используя метод Данилевского найти собственные числа и собственные вектора матрицы А. Разрешается реализовывать метод Данилевского средствами MathCAD или Mathematica (корни характеристического уравнения найти с помощью встроенных функций). Метод Данилевского можно реализовать также на VBA (корни характеристического уравнения найти с помощью команды «Поиск решения» или «Подбор параметра» пункта меню Сервис в Excel).
2. Используя метод итераций, определить первое собственное число матрицы (наибольшее по модулю). Найти соответствующий ему собственный вектор, имеющий кубическую норму, равную 1. Метод итераций реализовать на языке программирования.
3. Сравнить результаты, полученные методом Данилевского и методом итераций.
Варианты заданий
№1. A = 
№3. A = 
№5. A = 
№7. A = 
№9. A = 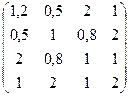
№11. A = 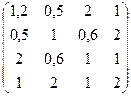
№13. A = 
№15. A = 
№17. A = 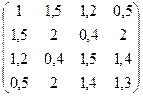
№19. A = 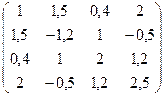
№21. A = 
№23. A = 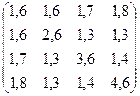
№25. A = 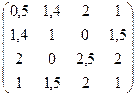
№27. A = 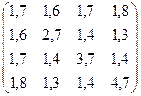
№29. A = 
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Методы решения задач о собственных
значениях и векторах матриц
Видео:Собственные значения и собственные векторыСкачать

Постановка задачи
Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math] . Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math] , удовлетворяющий условию
называется собственным вектором матрицы [math]A[/math] . Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math] .
Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:
Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math] ) при условии [math]|A-lambda E|=0[/math] . Это равенство есть характеристическое уравнение:
где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math] , а соответствующие каждому собственному значению [math]lambda_i,
i=1,ldots,n[/math] , ненулевые векторы [math]X^i[/math] , удовлетворяющие системе
являются собственными векторами.
Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.
Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.
Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_|lambda_i(A)|[/math] и [math]min_|lambda_i(A)|[/math] . Величина [math]rho(A)[/math] называется спектральным радиусом .
1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math] , то вектор [math]mu X^i[/math] , где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math] .
2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.
3. Симметрическая матрица имеет полный спектр [math]lambda_i,
i=overline[/math] , действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.
4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.
Видео:Собственные значения и собственные векторы. ТемаСкачать

Метод непосредственного развертывания
Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь
Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math] , вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math] , при которых [math]P_n(lambda_i)=0
(i=overline)[/math] . Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,
i=overline[/math] . Эти решения [math]X^i[/math] , определенные с точностью до произвольной константы, образуют систему [math]n[/math] , вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.
Видео:7 4 Собственные векторы и собственные значенияСкачать

Алгоритм метода непосредственного развертывания
1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math] . Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.
2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math] . Для этого можно применить методы, изложенные далее.
3. Для каждого собственного значения составить систему (2.4):
и найти собственные векторы [math]X^i[/math] .
Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname(A-lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.
Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb^[/math] , где [math]A=begin3&-2\-4&1end[/math] .
1. Запишем уравнение (2.5): [math]|A-lambda E|= begin3-lambda&-2\-4& 1-lambda end= lambda^2-4 lambda-5=0[/math] , отсюда получаем характеристическое уравнение [math]P_2(lambda)equiv lambda^2-4 lambda-5=0[/math] .
2. Находим его корни (собственные значения): [math]lambda_1=5,
3. Составим систему [math](A-lambda_iE)X^i=0,
i=1,2[/math] , для каждого собственного
значения и найдем собственные векторы:
Отсюда [math]x_1^1=-x_2^1[/math] . Если [math]x_2^1=mu[/math] , то [math]x_1^1=-mu[/math] . В результате получаем [math]X^1= bigl^T= bigl^T[/math] .
Для [math]lambda_2=-1[/math] имеем
Отсюда [math]x_2^2=2x_1^2[/math] . Если [math]x_1^2=mu[/math] , то [math]x_2^2=2mu[/math] . В результате получаем [math]X^2= bigl^T= bigl^T[/math] , где [math]mu[/math] — произвольное действительное число.
Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin2&-1&1\-1&2&-1\0&0&1end[/math] .
1. Запишем характеристическое уравнение (2.5):
2. Корни характеристического уравнения: [math]lambda_=1[/math] (кратный корень), [math]lambda_3=3[/math] — собственные значения матрицы.
3. Найдем собственные векторы.
Для [math]lambda_=1[/math] запишем систему [math](A-lambda_E)cdot X^=0colon[/math]
Поскольку [math]operatorname(A-lambda_E)=1[/math] , в системе имеется одно независимое уравнение
x_3^=3[/math] , получаем [math]x_1^=1[/math] и собственный вектор [math]X^1= begin1&1&0end^T[/math] .
x_3^=1[/math] , получаем [math]x_1^=-1[/math] и другой собственный вектор [math]X^2= begin-1&0&1end^T[/math] . Заметим, что оба собственных вектора линейно независимы.
Для собственного значения [math]lambda_3=3[/math] запишем систему [math](A-lambda_3E)cdot X^3=0colon[/math]
Поскольку [math]operatorname(A-lambda_3E)=2[/math] , то выбираем два уравнения:
x_1^3=-x_2^3[/math] . Полагая [math]x_2^3=1[/math] , получаем [math]x_1^3=-1[/math] и собственный вектор [math]X^3=begin-1&1&0 end^T[/math] .
Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Метод итераций для нахождения собственных значений и векторов
Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_bigl|lambda_i(A)bigr|[/math] .
Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,
i=1,ldots,n[/math] , и собственные значения матрицы [math]A[/math] таковы, что
Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Алгоритм метода итераций
1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math] .
lambda_1^= frac<x_i^><x_i^>[/math] , где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math] , и положить [math]k=1[/math] .
4. Найти [math]lambda_1^= frac<x_i^><x_i^>[/math] , где [math]x_i^, x_i^[/math] — соответствующие координаты векторов [math]X^[/math] и [math]X^[/math] . При этом может быть использована любая координата с номером [math]i,
1leqslant ileqslant n[/math] .
5. Если [math]Delta= bigl|lambda_1^- lambda_1^bigr|leqslant varepsilon[/math] , процесс завершить и положить [math]lambda_1cong lambda_1^[/math] . Если varepsilon»>[math]Delta>varepsilon[/math] , положить [math]k=k+1[/math] и перейти к пункту 3.
1. Процесс последовательных приближений
сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^[/math] стремится к собственному вектору [math]X^1[/math] . Действительно, разложим [math]X^[/math] по всем собственным векторам: [math]textstyle<X^= sumlimits_^ c_iX^i>[/math] . Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math] , то
При большом [math]k[/math] дроби [math]<left(fracright)!>^k, ldots, <left(fracright)!>^k[/math] малы и поэтому [math]A^kX^= c_1lambda_1^kX^1[/math] , то есть [math]X^to X^1[/math] при [math]ktoinfty[/math] . Одновременно [math]lambda_1= limlimits_ frac<x_^><x_^>[/math] .
2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.
3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.
4. При неудачном выборе начального приближения [math]X^[/math] предел отношения [math]frac<x_i^><x_i^>[/math] может не существовать. В этом случае следует задать другое начальное приближение.
5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.
6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.
7. Используя [math]lambda_1[/math] , можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac<x_i^- lambda_1 x_i^><x_i^- lambda_1 x_i^>
(i=1,2,ldots,n)[/math] . Эта формула дает грубые значения для [math]lambda_2[/math] , так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j
8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac<X^><|X^|_1>[/math] .
Пример 2.3. Для матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math] .
1. Выбирается начальное приближение собственного вектора [math]X^= begin 1&1&1 end^T[/math] . Положим [math]k=0[/math] .
5. Так как varepsilon»>[math]bigl|lambda_1^- lambda_1^bigr|= 0,!75> varepsilon[/math] , то процесс необходимо продолжить. Результаты вычислений удобно представить в виде табл. 10.10.
Точность по достигнута на четвертой итерации. Таким образом, в качестве приближенного значения [math]lambda_1[/math] берется 6,9559, а в качестве собственного вектора принимается [math]X^1= begin 2838& 1682& 1888end^T[/math] .
Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим
Согласно замечаниям, в качестве собственного значения [math]lambda_1[/math] матрицы можно взять не только отношение
а также их среднее арифметическое [math]fracapprox 6,!8581[/math] .
Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin2&-1&1\ -1&2&-1\ 0&0&3 end[/math] и соответствующий собственный вектор.
1. Зададим начальное приближение [math]X^= begin1&-1&1 end^T[/math] и [math]varepsilon=0,!0001[/math] .
Выполним расчеты согласно методике (табл. 10.11).
В результате получено собственное значение [math]lambda_1cong 3,!00003[/math] и собственный вектор [math]X^1= begin 88573&-88573&1end^T[/math] или после нормировки
Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Метод вращений для нахождения собственных значений
Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb^[/math] с помощью ортогональной матрицы [math]H[/math] .
Напомним, что две матрицы [math]A[/math] и [math]A^[/math] называются подобными ( [math]Asim A^[/math] или [math]A^sim A[/math] ), если [math]A^=H^AH[/math] или [math]A=HA^H^[/math] , где [math]H[/math] — невырожденная матрица.
В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^=H^H=E[/math] , т.е. [math]H^=H^[/math] . В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]
[math]operatorname
При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:
Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^,
ine j[/math] , определяется ортогональная матрица [math]H^[/math] , приводящая этот элемент [math]a_^[/math] (а также и [math]a_^[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^[/math] выбирается наибольший по модулю. Матрица [math]H^[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^[/math] и имеет вид
В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^= cosvarphi^[/math] и [math]h_^=cosvarphi^[/math] , а остальные элементы нулевые, за исключением [math]h_^=-sinvarphi^[/math] , [math]h_^=sinvarphi^[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).
Угол поворота [math]varphi^[/math] определяется по формуле
где [math]|2varphi^|leqslant frac,
i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).
В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^)[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^) . Однако элементы [math]a_^[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность sigma(A^)> ldots> sigma(A^)>ldots»>[math]sigma(A^)> sigma(A^)> ldots> sigma(A^)>ldots[/math] . Поэтому [math]sigma(A^)to0[/math] при [math]ktoinfty[/math] . Это и означает сходимость метода. При этом [math]A^to Lambda= operatorname(lambda_1,ldots,lambda_n)[/math] .
Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]<vec,vec>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]
Таким образом, для компонент [math]vec,’,, vec,'[/math] будем иметь [math]bigl(vec,’,vec,’bigr)= bigl(vec,vecbigr)cdot! begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.
Видео:Собственные значения и собственные векторы. ПримерСкачать

Алгоритм метода вращений
1. Положить [math]k=0,
A^=A[/math] и задать 0″>[math]varepsilon>0[/math] .
2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^[/math] максимальный по модулю элемент [math]a_^,
Если [math]|a_^|leqslant varepsilon[/math] для всех [math]ine j[/math] , процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^)=a_^,
Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:
Если varepsilon»>[math]bigl|a_^bigr|>varepsilon[/math] , процесс продолжается.
3. Найти угол поворота по формуле [math]varphi^= frac operatorname frac<2a_^><a_^-a_^>[/math] .
4. Составить матрицу вращения [math]H^[/math] .
5. Вычислить очередное приближение [math]A^= bigl(H^bigr)^T A^ H^[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.
1. Используя обозначение [math]overline
_k= frac<2a_^><a_^-a_^>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам
2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.
3. При [math]n=2[/math] для решения задачи требуется одна итерация.
Пример 2.5. Для матрицы [math]A=begin 2&1\1&3 end[/math] методом вращений найти собственные значения и собственные векторы.
1. Положим [math]k=0,
2°. Выше главной диагонали имеется только один элемент [math]a_=a_=1[/math] .
3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:
4°. Сформируем матрицу вращения:
5°. Выполним первую итерацию:
Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]sum_^a_^= sum_^a_^=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.
2. Максимальный по модулю наддиагональный элемент [math]|a_|= 4,!04620781325cdot10^ . Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:
Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] .
1. Положим [math]k=0,
2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_^=2[/math] . Так как varepsilon=0,!001″>[math]a_=2> varepsilon=0,!001[/math] , то процесс продолжается.
3°. Находим угол поворота:
4°. Сформируем матрицу вращения: [math]H^= begin0,!85065&0&-0,!52573\ 0&1&0\ 0,!52573&0&0,!85065 end[/math] .
5°. Выполним первую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!236&1,!376&2,!33cdot10^\ 1,!376&4&0,!325\ 2,!33cdot10^&0,!325&1,!764 end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.
2(1). Максимальный по модулю наддиагональный элемент [math]a_^=1,!376[/math] . Так как varepsilon=0,!001″>[math]a_^> varepsilon=0,!001[/math] , процесс продолжается.
3(1). Найдем угол поворота:
4(1). Сформируем матрицу вращения: [math]H^= begin 0,!902937&-0,!429770&0\ 0,!429770&0,!902937&0\ 0&0&1 end[/math] .
5(1). Выполним вторую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!891& 2,!238cdot10^&0,!14\ 2,!238cdot10^& 3,!345&0,!293\ 0,!14&0,!293&1,!764 end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.
2(2). Максимальный по модулю наддиагональный элемент varepsilon=0,!001″>[math]a_^=0,!293> varepsilon=0,!001[/math] .
3(2). Найдем угол поворота:
4(2). Сформируем матрицу вращения [math]H^= begin1&0&0\ 0&0,!9842924& -0,!1765460\ 0& 0,!1765460& 0,!9842924end[/math] .
5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:
2(3). Максимальный по модулю наддиагональный элемент varepsilon»>[math]a_^= 0,!138>varepsilon[/math] .
3(3). Найдем угол поворота:
4(3). Сформируем матрицу вращения: [math]H^= begin 0,!999646&0&-0,!026611\ 0&1&0\ 0,!026611&0&0,!999646 end[/math] .
5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:
2(4). Так как varepsilon»>[math]a_^=0,!025>varepsilon[/math] , процесс повторяется
3(4). Найдем угол поворота
4(4). Сформируем матрицу вращения: [math]H^= begin 0,!9999744&-0,!0071483&0\ 0,!0071483&0,!9999744&0\ 0&0&1 end[/math] .
5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:
2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]bigl|-6,!649cdot10^bigr| , процесс завершается.
Собственные значения: [math]lambda_1cong a_^= 6,!895,,
lambda_3cong a_^=1,!707,,[/math] . Для нахождения собственных векторов вычислим
X^3=begin-0,!473\-0,!171\0,!864 end[/math] или после нормировки
🔍 Видео
Собственные векторы и собственные значенияСкачать

Собственные значения матрицыСкачать

Собственные векторы и собственные числа линейного оператораСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Матрицы и векторыСкачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Практика 1. Часть 1. Собственные вектора и значения линейного оператора. Канонический вид.Скачать

Итерационные предобусловленные методы в подпространствах Крылова: тенденции XXI-го векаСкачать

Матрицы: виды и действия над ними | Высшая математика | Линейная алгебра | TutorOnlineСкачать