Кто открыл медиану треугольника

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

We are checking your browser. gufo.me

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d97c8895a5d7b2b • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Видео:Все факты о медиане треугольника для ЕГЭСкачать

Медиана — это золотое сечение треугольника

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.

У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.

И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.

Видео:Построение медианы в треугольникеСкачать

Медиана — это.

Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.

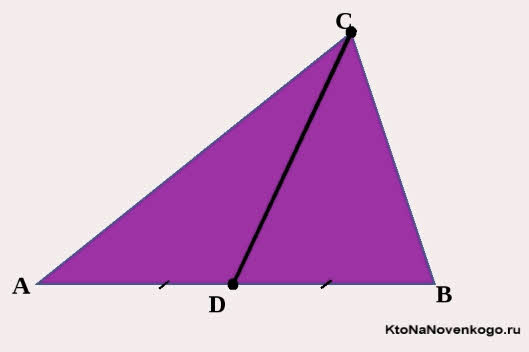
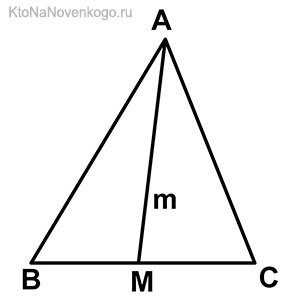
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.

Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.

Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.

Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:

Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.

Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.

И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!

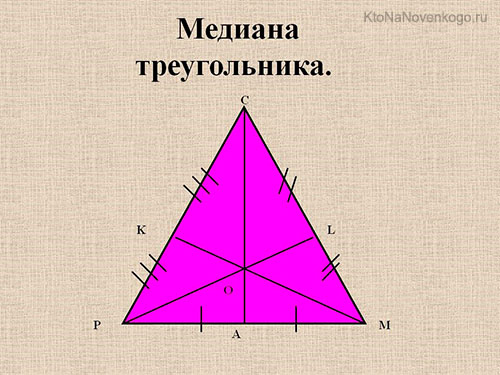
И выглядят они вот так.

На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.

Видео:🔥 Свойства МЕДИАНЫ #shortsСкачать

Пересечение медиан треугольника

Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.

Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.

Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.

Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:

1. Отрезок СО вдвое больше, чем отрезок АО;
2. Отрезок РО вдвое больше, чем отрезок LO;
3. Отрезок МО вдвое больше, чем КО.

Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.

Видео:8. Медиана треугольника и её свойства.Скачать

Медиана равностороннего треугольника

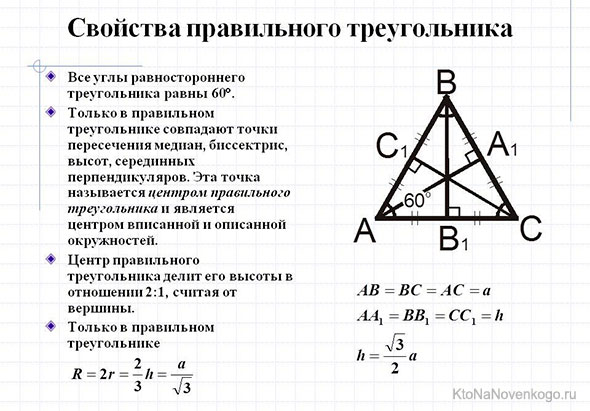
Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.

Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.

Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.

И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.

Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.

Видео:Длина медианы треугольникаСкачать

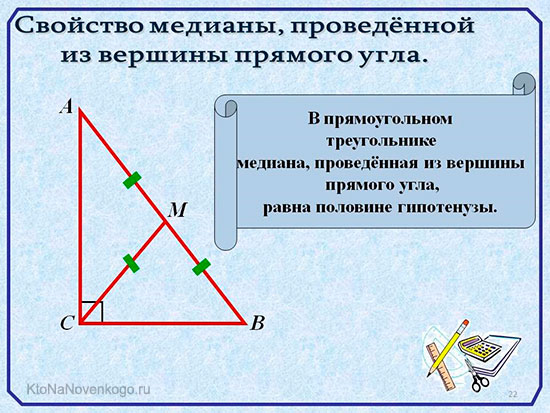
Медиана прямоугольного треугольника

Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.

Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.

Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.

Видео:Точка пересечения медиан в треугольникеСкачать

Вместо заключения

А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.

Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.

Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».

И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.

Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Теперь остаётся подумать над тем, как применить это знание о медиане на практике. Если придумаю, вдруг Нобелевскую премию дадут?

Видео:17. Медианы, биссектрисы и высоты треугольникаСкачать

Реферат: Медианы треугольника

Гомельская научно-практическая конференция школьников по математике, ее приложениям и информационным технологиям «Поиск»

Реферат на тему:

9′ класса государственного

Многопрофильная гимназия № 14»

Учитель математики высшей категории

Сафонова Алла Викторовна

1. Медианы треугольника и их свойства

2. Открытие немецкого математика Г. Лейбница

3. Применение медиан в математической статистике

4. Медианы тетраэдра

5. Шесть доказательств теоремы о медианах

Список использованных источников и литературы

Геометрия начинается с треугольника. Вот уже два тысячелетия треугольник является как бы символом геометрии, но он не символ. Треугольник – атом геометрии.

Треугольник неисчерпаем – постоянно открываются его новые свойства. Чтобы рассказать о всех известных его свойствах, необходим том сравнимый по объему с томом Большой энциклопедии. Мы хотим рассказать о медиане треугольника и ее свойствах, а так же о применении медиан.

Сначала вспомним, что медиана треугольника – это отрезок соединяющий вершины треугольника с серединой противоположной стороны. Медианы имеют множество свойств. Но мы рассмотрим одно свойство и 6 различных его доказательств. Три медианы пересекаются в одной точке, которая называется центроидом (центром масс) и делятся в отношении 2:1.

Существует медианы не только треугольника, но и тетраэдра. Отрезок, соединяющий вершину тетраэдра с центроидом (точкой пересечения медиан) противолежащей грани называется медианой тетраэдра. Мы так же рассмотрим свойство медиан тетраэдра.

Медианы используются в математической статистике. Например, для нахождения среднего значения некоторого набора чисел.

1. Медианы треугольника и их свойства

Как известно, медианами треугольника называются отрезки, соединяющие его вершины с серединами противоположных сторон. Все три медианы пересекаются в одной точке и делятся ею в отношении 1:2.

Точка пересечения медиан является также центром тяжести треугольника. Если подвесить картонный треугольник в точке пересечения его медиан то он будет находиться в состоянии равновесия

Любопытно, что вcе шесть треугольников, на которые всякий треугольник разбивается своими медианами, имеют одинаковые площади.

Медианы треугольника через его стороны выражаются так:

,

,

.

Если две медианы перпендикулярны, то сумма квадратов сторон, на которые они опущены, в 5 раз больше квадрата третьей стороны.

Построим треугольник, стороны которого равны медианам данного треугольника, тогда медианы построенного треугольника будут равны 3/4 сторон первоначального треугольника.

Данный треугольник назовем первым, треугольник из его медиан — вторым, треугольник из медиан второго — третьим и т. д. Тогда треугольники с нечетными номерами (1,3, 5, 7. ) подобны между собой и треугольники с четными номерами (2, 4, 6, 8. ) также подобны между собой.

Сумма квадратов длин всех медиан треугольника равняется ¾ суммы квадратов длин его сторон.

2. Открытие немецкого математика Г. Лейбница

Знаменитый немецкий математик Г. Лейбниц обнаружил замечательный факт: сумма квадратов расстояний от произвольной точки плоскости до вершин треугольника, лежащего в этой плоскости, равняется сумме квадратов расстояний от точки пересечения медиан до его вершин, сложенной с утроенным квадратом расстояния от точки пересечения медиан до выбранной точки.

Из этой теоремы следует, что точка на плоскости, для которой сумма квадратов расстояний до вершин данного треугольника является минимальной,- это точка пересечения медиан этого треугольника.

В то же время минимальная сумма расстояний до вершин треугольника (а не их квадратов) будет для точки, из которой каждая сторона треугольника видна под углом в 120°, если ни один из углов треугольника не больше 120° (точка Ферма), и для вершины тупого угла, если он больше 120°.

Из теоремы Лейбница и предыдущего утверждения легко найти расстояние d от точки пересечения медиан до центра описанной окружности. Действительно, это расстояние по теореме Лейбница равно корню квадратному из одной трети разности между суммой квадратов расстояний от центра описанной окружности до вершин треугольника и суммой

Квадратов расстояний от точки пересечения медиан до вершин треугольника. Получаем, что

.

Точка М пересечения медиан треугольника AВС является единственной точкой треугольника, для которой сумма векторов МА, MB и МС равна нулю. Координаты точки М (относительно произвольных осей) равны средним арифметическим соответствующих координат вершин треугольника. Из этих утверждений можно получить доказательство теоремы о медианах.

3. Применение медиан в математической статистике

Медианы бывают не только в геометрии, но и в математической статистике. Пусть нужно найти среднее значение некоторого набора чисел ,, . а_п . Можно, конечно, за среднее принять среднее арифметическое

Но иногда это неудобно. Допустим, что нужно определить средний рост второклассников Москвы. Опросим наугад 100 школьников и запишем их рост. Если один из ребят в шутку скажет, что его рост равен километру, то среднее арифметическое записанных чисел окажется слишком большим. Гораздо лучше в качестве среднего взять медиану чисел , . а_п .

Предположим, что чисел — нечетное количество, и расставим их в неубывающем порядке. Число, оказавшееся на среднем месте, называется медианой набора. Например, медиана набора чисел 1, 2, 5, 30, 1, 1, 2 равна 2 (а среднее арифметическое значительно больше — оно равно 6).

4. Медианы тетраэдра

Оказывается, можно говорить о медианах не только для треугольника, но и для тетраэдра. Отрезок, соединяющий вершину тетраэдра с центроидом (точкой пересечения медиан) противолежащей грани, называется медианой тетраэдра. Как и медианы треугольника, медианы тетраэдра пересекаются в одной точке, центре масс или центроиде тетраэдра, но отношение, в котором они делятся в этой точке, иное – 3:1, считая от вершин. Эта же точка лежит и на всех отрезках, соединяющих середины противоположных ребер тетраэдра, его бимедианах, и делит их пополам. Это можно доказать, например, из механических соображений, поместив в каждую из четырех вершин тетраэдра грузики единичной массы.

5. Шесть доказательств теоремы о медианах

Давно замечено, что познакомиться с разными решениями одной задачи бывает полезнее, чем с однотипными решениями разных задач. Одной из теорем, допускающих, как и многие другие классические теоремы элементарной геометрии, несколько поучительных доказательств, является

Теорема о медианах треугольника. Медианы , В и С треугольника ABC пересекаются в некоторой точке М, причем каждая из них делится этой точкой в отношении 2:1, считая от вершины: AM : M = BM : M = CM : M =2. (1)

Во всех приводимых далее доказательствах, кроме шестого, мы устанавливаем только, что медиана В проходит через точку М, которая делит медиану А в отношении 2:1. Если в соответствующем рассуждении заменить отрезок В на отрезок С, то мы получим, что и С проходит через М. Этим будет доказано, что все три медианы пересекаются в некоторой точке М, причем АМ:М — 2. Поскольку все медианы равноправны, можно заменить А на В или СС₁ отсюда вытекает (1).

Первое доказательство (8 класс).

Пусть К — середина отрезка AM , В’ — точка пересечения прямой ВМ со стороной АС. Нам достаточно доказать, что АВ’ = В’С. Через точки К и параллельно прямой ВМ проведем отрезки KL и N (рис. 1). Поскольку АК — КМ = М и С=В, по теореме Фалеса получаем

Рассмотрим гомотетию с центром М и коэффициентом -1/2. Точка А переходит при этой гомотетии в . Пусть В переходит в В’ (рис. 2). Тогда = — АВ. С другой стороны, средняя линия получается из стороны ВА при гомотетии с центром С и коэффициентом 1/2; таким образом:

=

Итак, , следовательно, В’=. Таким образом, треугольники ABC и гомотетичны, причем центр гомотетии лежит в точке М. По определению гомотетии, точки В, М и В’ = лежат на одной прямой.

Рассмотрим треугольники MAC и МС (рис. 3). Их высоты, опущенные из вершины С, совпадают, а длины противолежащих этой вершине сторон относятся как 2:1, поэтому , где S обозначает площадь. Аналогично, . Но . Следовательно,

. Таким образом, треугольники МАВ, МВС и МСА равновелики. Пусть В’ — точка пересечения прямых ВМ и АС. Докажем, что АВ’ = В’С. С одной стороны,

С другой стороны,

.

,

отсюда получаем

.

Четвертое доказательство (9 класс).

ВМ= ВС + СА+АМ=ВС + СА+

Следовательно, точка М лежит на медиане .

Пятое доказательство (9 класс).

Опять рассмотрим точку В’ пересечения прямых ВМ и АС (рис. 3). Применяя теорему синусов сначала к треугольникам АВ’В и СВ’В, а затем — к треугольникам АВМ и ВМ и учитывая, что sinAB ‘ B = sinCB ‘ B , sinAMB = = sinMB , BC=2Bи МА = 2M, получим

.

Шестое доказательство(10 класс).

Проведем через точки А и В плоскость а, не содержащую С, и построим в этой плоскости правильный треугольник ABC (рис. 5). Из общих свойств параллельной проекции следует, что параллельная проекция вдоль прямой С переводит треугольникАВС в треугольник АВ, причем медианы треугольника ABC проектируются в медианы треугольника AB . Но в правильном треугольнике медианы являются и биссектрисами, а следовательно, пересекаются в одной точке. Легко доказать также (докажите!), что для треугольника AB справедливы равенства (1).

Отсюда вытекает, что наша теорема верна и для треугольника АВС.

Упомянем еще одно, быть может, самое простое и естественное доказательство теоремы о медианах: если поместить в вершины треугольника равные массы и поочередно группировать их парами, мы получим, что центр всех трех масс лежит на каждой из медиан. Центр системы равных масс, помещенных в некоторые точки, называется центроидом этого набора точек, поэтому и точку пересечения медиан треугольника часто называют его центроидом.

Исходя из проделанной работы можно сделать следующие выводы:

1. Одну теорему можно доказать разными способами. Это гораздо полезнее. Ведь ее можно изучить с разных сторон, используя различные методы и темы курса 8-10 классов.

2. Медиана была изучена многими учеными, но особый вклад в ее развитие внес немецкий ученый Г. Лейбниц. Он обнаружил замечательный факт: сумма квадратов расстояний от произвольной точки плоскости до вершин треугольника, лежащего в этой плоскости, равняется сумме квадратов расстояний от точки пересечения медиан до его вершин, сложенной с утроенным квадратом расстояния от точки пересечения медиан до выбранной точки.

Из этой теоремы следует, что точка на плоскости для которой сумма квадратов расстояний до вершин данного треугольника является минимальной, — это точка пересечения медиан этого треугольника.

3. Медианы используются не только в геометрии, но и в физике, и в статической математике. Для вычисления среднего арифметического и др.

Список использованных источников и литературы

1. И.Л. Никольская. Факультативный курс по математике. Учебное пособие для 7-9 классов средней школы. Москва “Просвещение” 1991 г. с. 92-93.

2. Т.Л. Рыбакова, И.В. Суслова. Школьный справочник “МАТЕМАТИКА”. Ярославль “Академия развития” 1997 г. с. 113.

3. Ежемесячный научно-популярный физико-математический журнал Академии наук СССР и Академии педагогических наук литературы. “ Квант № 7 1990 г. с. 40.

4. Ежемесячный научно-популярный физико-математический журнал Академии наук СССР и Академии педагогических наук литературы. “ Квант № 1 1990 г. с. 54.

1. Докажите, что точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной прямой. Вывести отсюда теорему о медианах.

3. Каждая из вершин пятиугольника соединена с серединой противолежащей стороны. Докажите, что если четыре из полученных прямых пересекаются в одной точке, то и пятая прямая проходит через эту точку.

4. Через каждое из ребер трехгранного угла и биссектрису противоположного плоского угла проведена плоскость. Докажите, что три полученные плоскости имеют общую прямую.

5. Точки A ₁ , B ₁ , C ₁ лежат соответственно на сторонах BC , CA и AB треугольника ABC . Известно, что отрезки AA ₁ , BB ₁ , CC ₁ пересекаются в точке P , причем

Докажите, что P — центроид треугольникаABC .

🔥 Видео

Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

Уравнения стороны треугольника и медианыСкачать

ГЕОМЕТРИЯ 8 класс. Свойство медиан треугольникаСкачать

Все свойства медианы в одной задаче.Скачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Медиана треугольника. Построение. Свойства.Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Медианы, биссектрисы и высоты треугольника | Геометрия 7-9 класс #18 | ИнфоурокСкачать

Формула медианы треугольникаСкачать

Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать