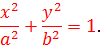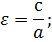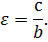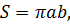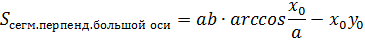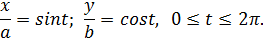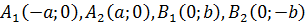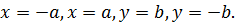Как построить эллипс по диаметру окружности (2 видео)

Приемы построения эллипса

Эллипс может быть построен как лекальная и как циркульная кривая.

Лекальная кривая строится по точкам, которые затем плавно соединяются от руки или при помощи лекала (способ 1).

Циркульная кривая строится при помощи циркуля как кривая, состоящая из четырёх сопрягающихся дуг окружностей (способы 2, 3).

Рассмотрим построение эллипса в аксонометрической плоскости х’О’у’. Аналогичными будут построения в других плоскостях. Только необходимо учитывать ориентацию осей эллипса. Возьмём окружность произвольного радиуса и построим её прямоугольную изометрию и диметрию разными способами, заготовив предварительно треугольники пропорциональности (рис. 84).

Способ L Лекальная кривая. Строим аксонометрию по восьми точкам, которыми будут являться концы осей и сопряжённых диаметров.

В прямоугольной изометрии (рис. 85, а) приведённые коэффициенты искажения по всем осям равны 1. Поэтому на осях х’ и у’ от центра О‘ откладываем радиус 7? окружности, на оси г’ — малую полуось эллипса 0,717?, на прямой, перпендикулярной z’, — большую его полуось 1,22R.

Для определения размеров большой и малой полуосей эллипса откладываем на натуральной шкале (1:1) треугольника пропорциональности для изометрии радиус окружности R, и из точки А проецируем его на остальные шкалы. На верхней шкале получаем размер 1,227?, на нижней — 0,71 R.

В прямоугольной диметрии (рис. 85, 6) по осям х’ и z’ коэффициент искажения равен 7, по оси у-0,5. Поэтому на оси х’ откладываем радиус R. Остальные размеры определяем при помощи треугольника пропорциональности для диметрии. На натуральной шкале (1:1) откладываем радиус R и через точку А и конец этого отрезка проводим проецирующий луч. На шкале 0,5 получаем размер 0,57? для оси у на шкале 0,35 — размер 0,357? малой полуоси эллипса, который откладываем на z’. Размер 1,067? большой полуоси берём со шкалы 1,06 и откладываем его на прямой, перпендикулярной z’.

Полученные восемь точек в обоих случаях предпочтительнее соединить при помощи лекала.

Примечание. Размеры осей эллипса для прямоугольной изометрии можно определить и графически (рис. 86). Для этого из концов С и D взаимно перпендикулярных диаметров окружности проводим дуги радиусом CD до взаимного пересечения в точках А и В. Соединив точки А и В, получим большую ось эллипса, равную 1,22D, а отрезок CD будет его малой осью, равной 0,7 Ш.

Способ 2. Коробовая кривая. Коробовая кривая является циркульной кривой, состоящей из четырёх дуг окружностей (рис. 87). Ею можно заменить эллипс. Строится она по его осям.

На рис. 87 коробовая кривая построена в прямоугольной изометрии. Малая ось CD направлена вдоль аксонометрической оси z большая АВ ей перпендикулярна. Построение выполняем в определённой последовательности.

• Соединяем концы большой и малой полуосей (отрезок A Q.
• Находим разность большой и малой полуосей (отрезок СЕ). Для этого из центра О‘ радиусом О’А проводим дугу до пересечения с прямой, проходящей через CD, в точке Е.
• Откладываем СЕ от точки С на АС. Получаем точку F.
• Строим срединный перпендикуляр к отрезку AF и отмечаем точки пересечения его с прямыми линиями, проходящими через оси эллипса. 0 и 0₂ — центры двух дуг окружностей.

На рис. 88 построена прямоугольная диметрия окружности в плоскости x’O’z’ в виде коробовой кривой. Малая ось CD направлена вдоль оси у’ и равна 0,95D. Большая ось АВ ±у’ и равна 1,060. Последовательность построения та же, что была рассмотрена выше для изометрии.

Этот метод является универсальным и может применяться не только для построения аксонометрии окружности, но и любого эллипса или овала, если известны размеры его большой и малой оси, чем широко пользуются при конструировании технических деталей.

Способ 3. Овал. Построим прямоугольную изометрию окружности в плоскости х’О’у’, заменяя эллипс овалом (рис. 89)

Задаём аксонометрические оси х’, у’, z’ и направление большой оси эллипса (перпендикулярно z’). Из центра эллипса проводим окружность радиусом, равным радиусу той окружности, аксонометрию которой строим. На пересечении этой окружности с направлением малой оси эллипса (осью z’) получаем два центра дуг 0 и 0₂. Проводим прямые через 0 и точки Е, L (или через 0₂ и точки К, F) пересечения окружности с осями х’, у’. На пересечении их с направлением большой оси получаем ещё два центра — 0₃ и 0₄. Затем последовательно проводим из центра 0 дугу EL радиусом 0Е, из центра 0₄ — дугу LF радиусом Оф?, из 0₂ — дугу FK радиусом 0₂F, из 0₃ — дугу КЕ радиусом 0₂К. Построенный овал неточно повторяет форму эллипса. У них имеются небольшие расхождения в размерах. Таким приёмом можно построить овал только в прямоугольной изометрии.

На рис. 90 показано построение овала, заменяющего эллипс в прямоугольной диметрии. Овал строится по осям и пригоден только для эллипсов, у которых малая ось в три раза меньше большой оси (в плоскостях х’О’у’иг’ОУ). Рассмотрим построение овала в плоскости х’О’у’.

Проводим две взаимно перпендикулярные прямые. Одну вертикально (параллельно z% другую горизонтально. Точка пересечения прямых будет центром О эллипса. Отрезки АВ и CD — соответственно большая и малая ось эллипса. По обе стороны от центра О на прямой, проходящей через малую ось CD, откладываем отрезки, равные длине большой оси АВ эллипса. Получаем центры 0 и 0₂ двух дуг окружностей. Центры 0₃ и 0₄ двух других дуг окружностей удалены от концов А и В большой оси эллипса на расстояние 1/4CD. Соединяем попарно центры и между линиями центров проводим дуги: из 0 радиусом Оф, из 0₄ радиусом О4В, из 0₂ радиусом 0₂С, из 0₃ радиусом 6М. Как следует из построений, радиусы сопрягающихся дуг равны R = АВ + 1/2CD, г = 1/4CZ).

Коробовая кривая и овал представляют собой кривые, приближенные к эллипсу. Существуют и другие способы построения эллипса.

Содержание

Эллипс — свойства, уравнение и построение фигуры
Определение и элементы эллипса
Основные свойства эллипса
Уравнение эллипса
Площадь эллипса
Площадь сегмента эллипса
Длина дуги эллипса
Радиус круга, вписанного в эллипс
Радиус круга, описанного вокруг эллипса
Как построить эллипс
Способы построения эллипса
💡 Видео

Видео:Как начертить овал. Уроки черчения.Скачать

Эллипс — свойства, уравнение и построение фигуры

Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Определение и элементы эллипса

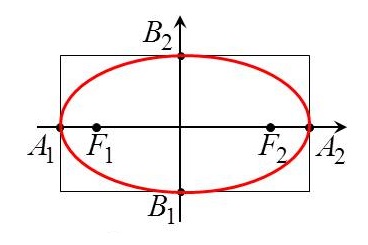
Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.

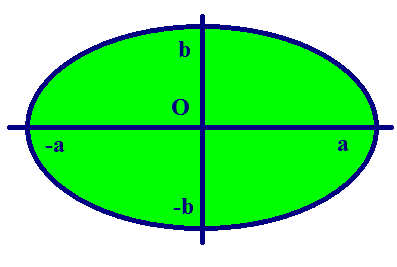
По форме график эллипса представляет замкнутую овальную кривую:

Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.

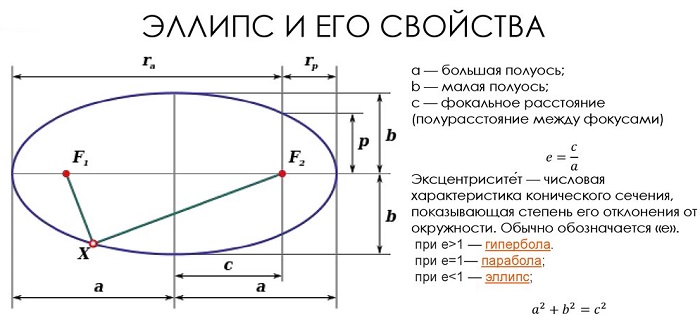
Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.

Точки эллипса, являющиеся концами осей, называются вершинами.

Расстояния от точки на линии до фокусов получили название фокальных радиусов.

Расстояние между фокусами есть фокальное расстояние.

Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Основные свойства эллипса

имеются две оси и один центр симметрии;

при равенстве полуосей линия превращается в окружность;

все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.

Видео:Эллипс - Инженерная графика.Скачать

Уравнение эллипса

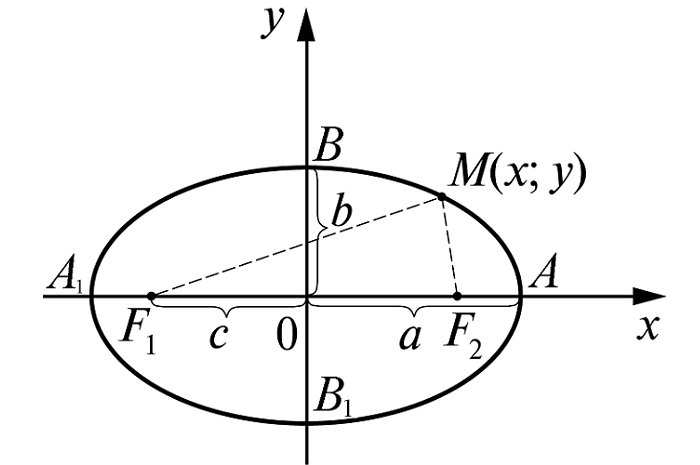
Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

Для составления уравнения достаточно воспользоваться определением, введя обозначение:

а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);

c – половина фокального расстояния;

M(x;y) – произвольная точка линии.

В этом случае фокусы находятся в точках F₁(-c;0); F₂(c;0)

После ввода ещё одного обозначения

получается наиболее простой вид уравнения:

a 2 b 2 — a 2 y 2 — x 2 b 2 = 0,

a 2 b 2 = a 2 y 2 + x 2 b 2 ,

Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).

В случае (b b) формула эксцентриситета (ε) принимает вид:

Чем меньше эксцентриситет, тем более сжатым будет эллипс.

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Площадь эллипса

Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:

a – большая полуось, b – малая.

Видео:КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВСкачать

Площадь сегмента эллипса

Часть эллипса, отсекаемая прямой, называется его сегментом.

Видео:Как начертить эллипс. Уроки черчения.Скачать

Длина дуги эллипса

Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Радиус круга, вписанного в эллипс

В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:

Видео:Как начертить овал в горизонтальной плоскостиСкачать

Радиус круга, описанного вокруг эллипса

Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:

Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.

Видео:Как начертить овал во фронтальной плоскостиСкачать

Как построить эллипс

Построение линии удобно выполнять в декартовых координатах в каноническом виде.

Строится прямоугольник. Для этого проводятся прямые:

Сглаживая углы, проводится линия по сторонам прямоугольника.

Полученная фигура есть эллипс. По координатам отмечается каждый фокус.

При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.

Видео:Как начертить эллипс (овал) на потолкеСкачать

Способы построения эллипса

Для изложения дальнейшей части курса необходимо вспомнить способы построения эллипсов.

На рис. 20 и 21 показаны способы построения эллипса по его главным осям, а на рис. 22, 23, 23′ даны способы построения эллипса по двум сопряженным диаметрам а₀Ь₀ и c₀d₀.

Напомним, что диаметр а₀Ь₀ (см. рис. 22), сопряженный данному диаметру c₀d₀, делит пополам хорды, параллельные диаметру c₀d₀, и наоборот.

Для построения эллипса по заданным его главным осям на рис. 20 описаны две вспомогательные окружности.

Диаметр большой окружности принят равным большой оси эллипса, а диаметр малой окружности равен малой оси эллипса.

Разделив большую окружность на произвольное число частей, намечаем на ней точки 1, 2, 3, 4, . . Соединяя затем точки 1, 2, 3, 4, . . с центром О, получаем на малой окружности точки 1_1з 2_Ь 3_1з 4_1з . .

Закончив это предварительное построение, проводим из точек 1, 2, 3, 4, . вертикальные линии, а из точек 1₁₅ 2_1з 3_1з 4_1з . горизонтальные линии до пересечения с проведенными уже из точек 1, 2, 3, 4, . вертикальными линиями.

Полученные в местах пересечения точки 1₀, 2₀, 3₀, 4₀, . соединяем по лекалу и этим самым намечаем очертание эллипса, отвечающего заданным осям а₀Ъ₀ и c₀d₀ (см. рис. 20). Нетрудно видеть, что проделанное построение сводится по существу к построению эллипса как фигуры, родственной двум построенным окружностям. Действительно, если принять большую ось эллипса а₀Ь₀ за ось родства, а точки с₀ и с, расположенные на продолжении малой оси, — за родственные точки при совмещенных центрах родственной окружности и эллипса в точке О, то можно рассматривать точки эллипса 1₀, 2₀, 3₀, 4₀, . как точки, родственные точкам окружности 1, 2, 3, 4, . .

В самом деле, если обозначить большую полуось а₀О эллипса через R, а малую полуось с₀О — через г, то

Рис. 23‘

Нетрудно усмотреть, что точно в таком же отношении точки 1₀, 2₀, 3₀, 4₀, . делят хорды, параллельные вертикальной оси сО. Например, для точки 1₀ из подобия треугольников HjIq и 1 On (см. рис. 20) можно написать такое же соотношение:

На рис. 21 показан другой способ построения эллипса по его главным осям.

В данном случае эллипс строится при помощи ключа пропорциональности (рис. 21, а). Для построения ключа откладываем по горизонтальной линии отрезок от произвольной величины и в точке о на перпендикуляре ос» к линии от откладываем размеры большой и малой полуосей эллипса. Намеченные в результате этого построения точки q и с» соединяем с точкой т. Делим далее отрезок от на несколько частей точками 1, 2, 3 и, проводя через точки деления 1, 2, 3 вертикальные линии 1 — 1″, 2 — 2″, 3 — 3″, намечаем на линиях тс₁ и тс» отрезки, пропорциональные отрезкам линии от.

После построения ключа пропорциональности переходим к определению точек 1₀, 2₀, 3₀, принадлежащих эллипсу.

Для этой цели описываем радиусом о₀а₀ окружность (рис. 21, б) и, перенося на нее точки 1″, 2″, 3″. намечаем точки 1′, 2′, 3‘. . После этого точки эллипса 1₀, 2₀, 3₀, . будут найдены в местах пересечения вертикальных линий 1′ — 1₀, 2′ — 2₀, 3′ — 3₀, . с горизонтальными линиями 1_х — 1₀, 2_г — 2₀, 3₁ — 3₀, . .

Убедиться в том, что фигура а₀1о2₀3₀с₀3₀. есть эллипс, можно следующим способом.

Принимаем ось а₀Ь₀ за ось абсцисс X, а ось о₀с’ —за ось ординат Y.

Тогда можно будет написать для какой-либо точки эллипса, например для точки 3₀, и соответствующей точки (3′), отношение ординат в таком виде:

Подставляя эти значения в уравнение (34), получаем откуда

Следовательно, для данного ключа отношение ординат точек окружности 7′, 2′, 3′. к ординатам точек кривой 1₀, 2₀, 3₀. есть величина постоянная. Уравнение окружности может быть выражено через координаты X и Y принадлежащих ей точек, в частности через координаты точки 3′, следующим образом:

Подставляя сюда значение уу, выраженное через ординату у_3о в (36), получим:

или после преобразования будем иметь

т. е. уравнение эллипса, имеющего полуоси: что и требовалось доказать.

На рис. 22 показано построение эллипса по его двум сопряженным диаметрам а₀Ь₀ и c₀d₀, заданным по величине и по направлению. Нетрудно видеть, что в данном случае эллипс также рассматривается как фигура, родственная окружности, описанной на его диаметре а₀Ь₀. Направление родства определяется путем соединения точки окружности с с концом с₀ сопряженного диаметра c₀d₀. Диаметр c₀d₀ в данном случае будет родственным диаметру окружности cd, а хорды 1₀ — 8₀, 2₀ — 7₀, 3₀ — 6₀, . родственны соответственно одноименным хордам окружности. Точки эллипса 1₀, 2₀, с₀, 3₀, 4₀, . оказываются в этом случае родственными точкам 1, 2, 3, с, 3, 4, . окружности. Число точек на окружности может быть взято произвольно.

На рис. 23 и 23′ показан другой способ построения эллипса по двум его сопряженным диаметрам. Этот способ основан на свойствах аффинного преобразования отрезков сторон квадрата, описанного около окружности, в аффинно соответствующие им отрезки сторон паралле- лограма, построенного на сопряженных диаметрах эллипса, родственного данной окружности.

Осью родства на рис. 23 является линия a-Jo^ а направление родства параллельно линии ОО₀.

Построение ведем в такой последовательности (см. рис. 23′):

1) на сопряженных диаметрах а₀Ь₀ и c₀d₀ строим параллелограм ааjbjb;
2) делим сторону параллелограма аЪ на равные части точками 1, 2, 3 и 4 и на столько же равных частей делим диаметр c₀d₀ точками 11 > 2j, и
3) соединяем точки 1 и 2 с точкой а₀, а точки 3 и 4 — с точкой Ь₀;
4) из точек а₀ и Ь₀ проводим штрихпунктирные линии через точки 1_Ь 2₁ до пересечения с пунктирными линиями Ь₀4, Ь₀3, а₀1, а₀2;
5) соединяем плавной чертой полученные точки пересечения 1₀, 2₀, 3₀, 4₀, . и этим намечаем очертание искомого эллипса.

Построение главных осей эллипса

При построении косоугольной аксонометрической проекции окружности приходится определять величину и направление главных осей эллипса по заданным его сопряженным диаметрам (по величине и по направлению, см. табл. 37 в ч. 2).

В этом случае рекомендуется использовать следующий способ (рис. 24).

Радиусом OY₀ описываем четверть окружности и намечаем точку У₀ Соединяем точку Yq с точкой Х₀, являющейся концом сопряженного диаметра XqXq. Линию У₀‘Х₀ продолжаем в обе стороны за точки У₀‘ иХ₀.

Делим пополам отрезок YqX₀ и из полученной точки с, как из центра, проводим полуокружность через центр эллипса О.

Точки тип пересечения этой полуокружности с линией YqX₀ лежат на главных осях эллипса. При этом отрезок тХ₀ = а равен по величине большой полуоси эллипса От₀, а отрезок пХ₀ = b равен малой полуоси эллипса Ол₀.

Вычерчивание эллипса при помощи кругов кривизны

Для приближенного построения эллипса можно применить прием, показанный на рис. 25. На главных осях т₀т₀ и п₀п₀ строим прямоугольник.

Соединив точку п₀ с точками т₀ и т₀, опускаем на линии п₀ — т₀ перпендикуляры из точек а и Ь. Эти перпендикуляры в пересечении с главными осями намечают точки с, с_г и с₂, являющиеся центрами, из которых можно циркулем описать значительную часть очертания эллипса. Участки, отмеченные пунктиром, должны быть соединены при этом по лекалу или на глаз от руки.