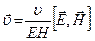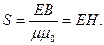Какова взаимная ориентация векторов в электромагнитной волне

Видеоурок: Опыты Герца. Свойства электромагнитных волн

Лекция: Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме

Опыты Максвелла доказали, что электрический ток в вакууме распространяется со скоростью, с которой движется свет, то есть 3*10 8 м/с.

При движении зарядов, которые создают ток, образуется две составляющих поля — электрическое и магнитное поле.

Опыт Герца

Чем быстрее будет происходить перемещение заряда, тем выразительнее будут электромагнитные волны. То есть, чем больше частота, тем большая интенсивность электромагнитных волн.

На частоту колебательного контура влияет индуктивность и ёмкость составляющих элементов цепи. Определить её можно по следующей формуле:

Электромагнитные волны являются поперечными. Это значит, что колебания магнитного и электрического поля происходят в плоскостях, которые являются параллельными к распространению волны.

На графике можно рассмотреть электрическую и магнитную составляющую электромагнитной волны.

Стоит отметить, что силовые характеристики магнитного и электрического поля находятся под углом 90 градусов друг к другу.

На графике показана длина волны, которая обозначается λ. Для её определения необходимо воспользоваться формулой:

Правила электромагнитных волн

Электромагнитным волнам присущи все правила, справедливые для механических волн:

1. Стоит отметить, что электромагнитная волна способна отразиться от плотного металла.

2. Через диэлектрик электромагнитная волна проходит достаточно проблематично, поскольку она им поглощается.

3. Если электромагнитная волна переходит из одной среды в другую, которая отличается плотностью, то она способна преломиться.

Какова взаимная ориентация векторов в электромагнитной волне

называют абсолютным показателем преломления. С учетом последнего имеем

Следовательно, показатель преломления есть физическая величина, равная отношению скорости электромагнитных волн в вакууме к их скорости в среде.

Векторы E, H и v образуют правовинтовую систему.

Из уравнений Максвелла следует также, что в электромагнитной волне векторы E и H всегда колеблются в одинаковых фазах, причем мгновенные значения Е и H в любой точке связаны соотношением

Следовательно, E и H одновременно достигают максимума, одновременно обращаются в нуль и т.д.

От уравнений (3.2.1) можно перейти к уравнениям

где y и z при E и H подчеркивают лишь то, что векторы E и H направлены вдоль взаимно перпендикулярных осей у и z.

Уравнениям (3.2.3) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (ЭМВ одной строго определенной частоты), описываемые уравнениями

где E₀ и H₀ — соответственно амплитуды напряженностей электрического и магнитного полей волны; ω — круговая частота; k = . волновое число; φ — начальная фаза колебаний в точках с координатой x = 0. В уравнениях (3.2.4) начальные фазы одинаковы, т.е. колебания электрического и магнитного векторов в ЭМВ происходят в одинаковых фазах.

Из всего вышеизложенного можно сделать следующие заключения:

• векторы H, E и v взаимно перпендикулярны, т.к. K и v направлены одинаково;
• электромагнитная волна является поперечной;
• электрическая и магнитная составляющие распространяются в одном направлении;
• векторы H и E колеблются в одинаковых фазах.

Некоторые свойства электромагнитной волны

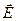
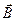
Электромагнитные волны представляют собой распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы и перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 46).

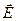
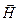
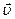
Так как векторы , и образуют правовинтовую тройку векторов, то их взаимная ориентация подчиняется правилу:

Для электромагнитной волны справедливы все формулы, закономерности и соотношения, которые были отмечены ранее для волновых процессов. Поэтому, согласно выражению (105), уравнение синусоидальной плоской электромагнитной волны, распространяющейся вдоль направления 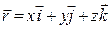, можно записать в виде:

Е (r,t) =Е₀ cos(w t – kr)

Волновое уравнение такой электромагнитной волны имеет вид:

= υ 2 ,

= υ 2 ,

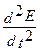
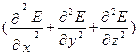
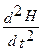
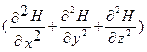
где υ — фазовая скорость электромагнитной волны. С помощью уравнений Максвелла было показано, что электромагнитные волны распространяются в веществе с конечной скоростью, определяемой по формуле:

. (127)

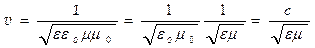
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные:

Скорость электромагнитных волн в вакууме (ε = μ = 1):

.

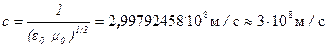
Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Равенство скорости распространения электромагнитных волн в вакууме скорости света в вакууме позволило Максвеллу предположить, что свет имеет электромагнитную природу.

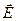
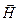
Электромагнитная волна называется монохроматической,если проекции её векторов и на оси прямоугольной системы координат совершают гармонические колебания одинаковой частоты.

В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Объемная плотность энергии электромагнитного поля в линейной изотропной среде

, (128)

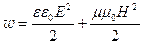
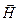
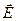
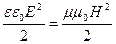
В электромагнитной волне модули напряженности магнитного поля и напряженности электрического поля в каждой точке пространства связаны соотношением

. (129)

Из уравнения (129) следует, что

, (130)

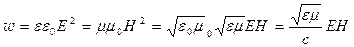
где с –скорость электромагнитных волн в вакууме.

Электромагнитные волны переносят энергию.

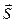
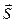
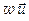
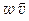
Плотностью потока энергии называют энергию, переносимую волной за единицу времени через единицу площади. Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойнтинга . Согласно формуле (112), имеем:

= = .

Для монохроматической волны групповая и и фазовая υ скорости равны. Подставляя сюда выражения (128) для w и (127) для υ, можно получить:

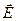
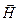
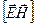
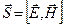
Так как векторы и взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН:

(131)

Единицей плотности потока энергии в СИ является Ватт на квадратный метр (Вт/м 2 ).

Так как интенсивность бегущей электромагнитной волны это физическая величина J, равная модулю среднего значения вектора Умова- Пойнтинга за период его полного колебания, то

| υ|, (132)

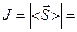
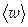
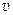
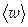
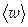
где -фазовая скорость, -среднее значение объемной плотности энергии. Согласно выражению (113), интенсивность волны пропорциональна квадрату амплитуды. Так как , согласно выражению (130), пропорциональна Е₀ 2 , то этот вывод справедлив и для электромагнитной волны: интенсивность электромагнитной волны пропорциональна квадрату амплитуды.

Дата добавления: 2015-07-18 ; просмотров: 667 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ