К двум непересекающимся окружностям равных радиусов проведены две параллельные общие касательные. Окружности касаются одной из этих прямых в точках A и B Через точку C, лежащую на отрезке AB, проведены касательные к этим окружностям, пересекающие вторую прямую в точках D и E, причём отрезки CA и CD касаются одной окружности, а отрезки CB и CE — другой.
а) Докажите, что периметр треугольника CDE вдвое больше расстояния между центрами окружностей.
б) Найдите DE, если радиусы окружностей равны 5, расстояние между их центрами равно 18, а AC = 8.
а) Пусть O1 — центр окружности, которая касается отрезка CD, O2 — центр окружности, которая касается отрезка CE, R — радиус окружностей. Окружность с центром O1 касается отрезка CD в точке K, а прямой DE в точке M; окружность с центром O2 касается отрезка CE в точке L, а прямой DE в точке N (рис. 1).
Тогда периметр треугольника CDE
б) Точка O1 лежит на биссектрисах углов MDC и ACD (рис. 2), следовательно,
В прямоугольном треугольнике CO1D имеем:
Аналогично, Получаем, что
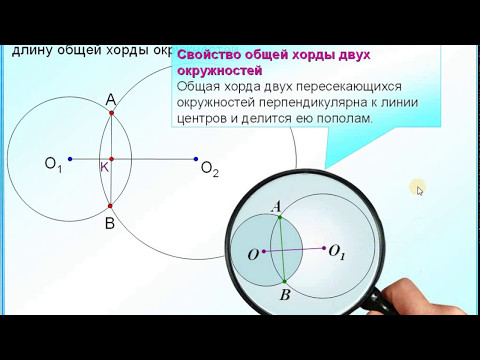
Задача: Радиусы двух пересекающихся окружностей равны 13 и 15, а общая хорда равна 24. Найдите расстояние между центрами. Дано: АО1=13 АО2=15 АВ=24 О1О2-? Решение: Пусть окружность радиуса 13 с центром О1 и окружность радиуса 15 с центром О2пересекаются в точках А и В. Тогда О1 О2 АВ и прямая О1 О2проходит через середину М отрезка АВ. О1. О2. A. A. M. M. О1. О2. B. B. Рис 2. Рис 1.
Слайд 6 из презентации «Расположение двух окружностей 7 класс»
Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Расположение двух окружностей 7 класс.pptx» можно в zip-архиве размером 596 КБ.
Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

Окружность
«Окружность 7 класс» — Вводная беседа «В мире окружностей». Построения циркулем и линейкой. Окружность произвольного радиуса. Цели урока. Любые две точки окружности делят ее на две части. Окружность. У круга есть одна подруга. Провести окружность произвольного радиуса. Работа с учебником по изучению материала. По готовым рисункам определить радиусы, хорды, диаметры, дуги.
«Числовая окружность» — 4. Аналитическая запись дуги числовой окружности. Положительные числа. Макет 2: третьи части дуг четвертей. 1. Числовая прямая. Макет 1: середины дуг четвертей. Числовая прямая. 2. Движение по числовой окружности. 3. Аналитическая запись дуги числовой окружности. Отметьте заданные точки на числовой окружности:
«Окружность 8 класс» — Теорема. В любой треугольник можно вписать окружность. Вписанная окружность. Проведем перпендикуляры ОК, ОL и ОM к сторонам ?АВС. Следствия: Проведем биссектрисы треугольника, пересекающиеся в точке О.
««Окружность» геометрия» — Градусная мера. Теорема о пересечении высот треугольника. Окружность, вписанная в многоугольник. Прямая, проходящая через середину данного отрезка. Теорема об отрезках пересекающихся хорд. Угол, вершина которого лежит на окружности. Прямая, имеющая с окружностью только одну общую точку. Теорема о биссектрисе угла.
«Длина окружности 6 класс» — Девиз урока: «Формулу окружности узнаем, Земной экватор сразу рассчитаем». Актуализация знаний. Диаметр колеса тепловоза равен 180 см. На готовых моделях окружностей определить длины окружности и диаметра с помощью нити. Диаметр земного шара приближенно равен 12,7 тыс. км. Задача урока. Цели урока. Число округлите до десятых.
«Окружность круг 5 класс» — Радиус – это…. ОВ, ОА, ОС- радиусы АС- диаметр. ВА — дуга. Презентация по теме: «Окружность и круг». Дополните предложение: Окружность. Радиус. АВ — дуга. Тема: Окружность и круг. Диаметр. Диаметр равен… Назовите получившиеся дуги. Точка О – центр окружности. 22.12.2011. 5 класс. Окружность и круг — …. У окружности и круга есть — …
Видео:Математика Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояние между ихСкачать

Конспект к уроку математики с презентацией на тему «РАЗЛИЧНЫЕ ЗАДАЧИ НА ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ОКРУЖНОСТЕЙ НА ПЛОСКОСТИ»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Документ Microsoft Word.docx
12.12(13.12) Различные задачи на взаимное расположение
ОКРУЖНОСТЕЙ НА ПЛОСКОСТИ
Цели: обобщить и систематизировать знания учащихся о взаимном расположении окружностей на плоскости.
Радиус большей окружности равен 3,5 см, радиус меньшей — 1,8 см.
Найдите расстояние между центрами окружностей .
Две окружности на плоскости либо пересекаются, либо не пересекаются.
Если одна окружность проходит через центр другой окружности, то такие окружности пересекаются.
Концентрические окружности — это окружности с общим центром.
Две окружности, радиусы которых различны, могут касаться внутренним и внешним образом.
Две окружности с равными радиусами могут касаться внутренним и внешним образом.
Если окружности пересекаются, то расстояние между их центрами меньше суммы радиусов.
Если окружности не пересекаются, то расстояние между их центрами больше суммы радиусов.
У концентрических окружностей радиусы равны.
Если окружности касаются внутренним образом, то расстояние между их центрами равно разности радиусов.
Если расстояние между центрами окружностей равно сумме их радиусов, то эти окружности касаются внешним образом.
Можно провести только две окружности с общим центром, которые пересекали бы данную окружность.
Можно провести только две окружности с общим центром, которые касались бы данной окружности.
Формирование умений и навыков .
Это задание можно выполнять по вариантам. Разделить учащихся по вариантам и дать каждому рассмотреть по два случая взаимного расположения окружностей и построения к ним общих касательных.
Учащиеся выполняют задание самостоятельно у себя в тетрадях, а затем представитель каждого варианта выходит к доске и, поясняя свои рассуждения, показывает, сколько общих касательных можно провести к данным окружностям. Остальные учащиеся могут поправлять и дополнять его ответ.
вариант — случаи а) и е).
вариант — случаи б) и д).
вариант — случаи в) и г).
После ответов учащихся всех трех вариантов делаются выводы о количестве общих касательных в каждом случае взаимного расположения двух окружностей на плоскости.
Как могут располагаться две окружности на плоскости?
Как связаны радиусы окружностей с расстоянием между их центрами в каждом случае взаимного расположения окружностей?
Сколько общих касательных можно провести к двум окружностям на плоскости в зависимости от их взаимного расположения?
Выбранный для просмотра документ урок-2.pptx
Описание презентации по отдельным слайдам:
Устная работа Радиус большей окружности равен 3,5 см, радиус меньшей — 1,8 см. Найдите расстояние между центрами окружностей. http://aida.ucoz.ru
Тест (Условные обозначения: «да» -˄ , «нет» -). 1)Две окружности на плоскости либо пересекаются, либо не пересекаются. 2)Если одна окружность проходит через центр другой окружности, то такие окружности пересекаются. 3)Концентрические окружности — это окружности с общим центром. 4)Две окружности, радиусы которых различны, могут касаться внутрен¬ним и внешним образом. http://aida.ucoz.ru
http://aida.ucoz.ru Тест 5)Две окружности с равными радиусами могут касаться внутренним и внешним образом. 6)Если окружности пересекаются, то расстояние между их центрами меньше суммы радиусов. 7)Если окружности не пересекаются, то расстояние между их центрами больше суммы радиусов. 8)У концентрических окружностей радиусы равны.
Тест 9)Если окружности касаются внутренним образом, то расстояние между их центрами равно разности радиусов. 10)Если расстояние между центрами окружностей равно сумме их радиусов, то эти окружности касаются внешним образом. 11)Можно провести только две окружности с общим центром, которые пересекали бы данную окружность. 12)Можно провести только две окружности с общим центром, которые касались бы данной окружности. http://aida.ucoz.ru
Ключ .__.__.˄.˄.__.˄.__.__.˄.˄.__.˄ http://aida.ucoz.ru
http://aida.ucoz.ru Домашнее задание. № 423, №427(а).
Решение задач № 421; № 422; http://aida.ucoz.ru
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 964 человека из 79 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 677 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 311 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 523 339 материалов в базе
Материал подходит для УМК
«Математика», Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др. / Под ред. Дорофеева Г.В., Шарыгина И.Ф.
Другие материалы
- 09.01.2018
- 16362
- 2052
- 09.01.2018
- 363
- 1
- 09.01.2018
- 3984
- 257
- 09.01.2018
- 805
- 31
- 09.01.2018
- 6353
- 67
- 09.01.2018
- 1449
- 10
- 09.01.2018
- 647
- 7
- 09.01.2018
- 248
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.01.2018 1219
- ZIP 1.3 мбайт
- 14 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Бурчаева Нура Айндиевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 2 месяца
- Подписчики: 2
- Всего просмотров: 466737
- Всего материалов: 320
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Генпрокуратура проводит масштабную проверку в российских школах
Время чтения: 1 минута
В Москве отмечается беспрецедентный рост заболеваемости коронавирусом среди детей
Время чтения: 2 минуты
Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение
Время чтения: 1 минута
В Тюменской области школы и колледжи перевели на дистанционное обучение
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Ставропольских школьников с 1 по 8 класс перевели на дистанционное обучение
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🔥 Видео
Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Окружность. 7 класс.Скачать

ЕГЭ Задача 16 Пересекающиеся окружностиСкачать

7 класс, 23 урок, Примеры задач на построениеСкачать

Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать

Математика ОГЭ. Задача на доказательство. Задание №24. Две пересекающиеся окружности.Скачать

Две окружности пересекаются, если радиус одной ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Задача. Две окружности касаются внутренним образом.Скачать

Задача в задаче ПланиметрияСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Знакомство с окружностью | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии в задачах 7-8Скачать

Знакомство с окружностью | Задачи 11-20 | Решение задач | Волчкевич | Уроки геометрии в задачах 7-8Скачать