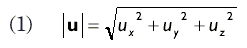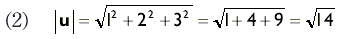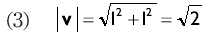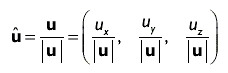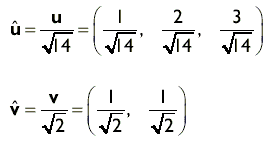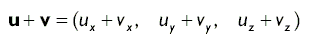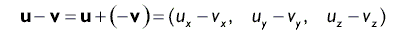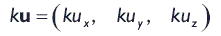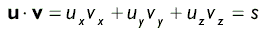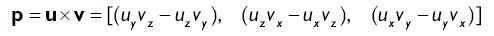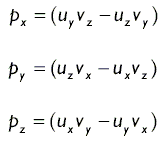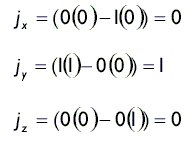Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
- Система координат в пространстве
- Плоскость в пространстве задается уравнением:
- Как построить вектор в трехмерном пространстве
- Что такое трехмерное пространство
- Понятие точки в трехмерном пространстве
- Разновидности систем координат
- Понятие прямой в трехмерном пространстве
- Определение векторов и базиса трехмерного пространства
- Зависимые и независимые векторы
- Плоскость в трехмерном пространстве
- Существует ли более трех измерений
- Заключение
- Равенство векторов
- Вычисление модуля вектора
- Решение
- Нормализация вектора
- Решение
- Сложение векторов
- Вычитание векторов
- Умножение вектора на скаляр
- Скалярное произведение векторов
- Векторное произведение
- Решение
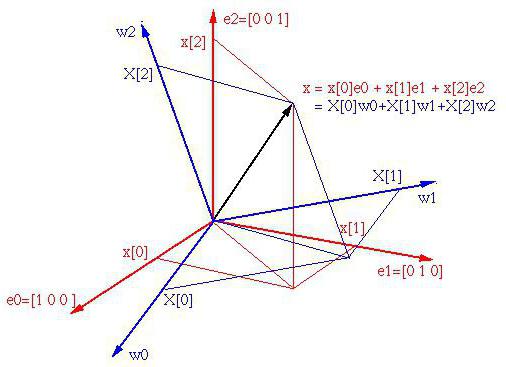
- Разложение вектора по базису
- Связь между базисами
- Что такое вектор
- Как построить вектор по двум точкам
- Как обозначают векторы
- Применяем векторы для решения задач физики
- 🎥 Видео
Видео:11 класс, 3 урок, Связь между координатами векторов и координатами точекСкачать

Система координат в пространстве
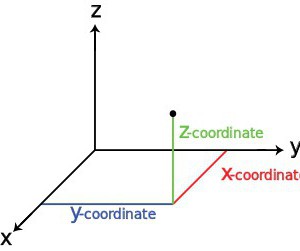
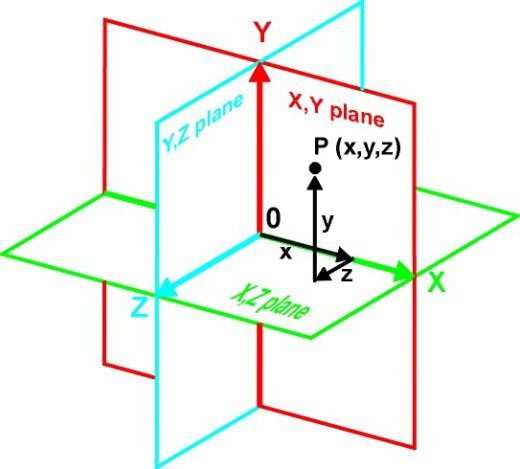
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Видео:Координаты точки и координаты вектора 1.Скачать

Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
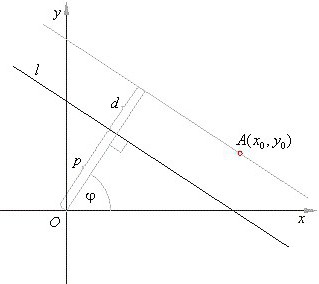
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Видео:Как построить точки в системе координат OXYZСкачать

Как построить вектор в трехмерном пространстве
Еще из школьного курса алгебры и геометрии мы знаем о понятии трехмерного пространства. Если разобраться, сам термин «трехмерное пространство» определяется как система координат с тремя измерениями (это знают все). По сути, описать любой объемный объект можно при помощи длины, ширины и высоты в классическом понимании. Однако давайте, как говорится, копнем несколько глубже.
Видео:Координаты вектора в пространстве. 11 класс.Скачать

Что такое трехмерное пространство
Как уже стало ясно, понимание трехмерного пространства и объектов, способных существовать внутри него, определяется тремя основными понятиями. Правда, в случае с точкой это именно три значения, а в случае с прямыми, кривыми, ломаными линиями или объемными объектами соответствующих координат может быть больше.
В данном случае все зависит именно от типа объекта и применяемой системы координат. Сегодня наиболее распространенной (классической) считается Декартова система, которую иногда еще называют прямоугольной. Она и некоторые другие разновидности будут рассмотрены несколько позже.
Кроме всего прочего, здесь нужно разграничивать абстрактные понятия (если можно так сказать, бесформенные) вроде точек, прямых или плоскостей и фигуры, обладающие конечными размерами или даже объемом. Для каждого из таких определений существуют и свои уравнения, описывающие их возможное положение в трехмерном пространстве. Но сейчас не об этом.
Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Понятие точки в трехмерном пространстве
Для начала определимся, что представляет собой точка в трехмерном пространстве. В общем-то, ее можно назвать некой основной единицей, определяющей любую плоскую или объемную фигуру, прямую, отрезок, вектор, плоскость и т. д.
Сама же точка характеризуется тремя основными координатами. Для них в прямоугольной системе применяются специальные направляющие, называемые осями X, Y и Z, причем первые две оси служат для выражения горизонтального положения объекта, а третья относится к вертикальному заданию координат. Естественно, для удобства выражения положения объекта относительно нулевых координат в системе приняты положительные и отрицательные значения. Однако же сегодня можно найти и другие системы.
Видео:9 класс, 3 урок, Связь между координатами вектора и координатами его начала и концаСкачать

Разновидности систем координат
Как уже говорилось, прямоугольная система координат, созданная Декартом, сегодня является основной. Тем не менее в некоторых методиках задания местоположения объекта в трехмерном пространстве применяются и некоторые другие разновидности.
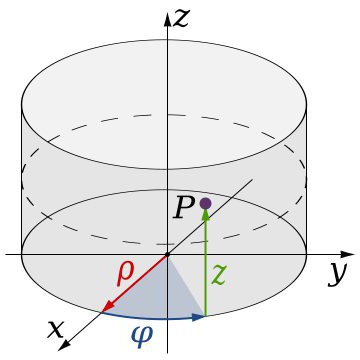
Наиболее известными считаются цилиндрическая и сферическая системы. Отличие от классической состоит в том, что при задании тех же трех величин, определяющих местоположение точки в трехмерном пространстве, одно из значений является угловым. Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.
Видео:91. Связь между координатами вектора и координатами его начала и концаСкачать

Понятие прямой в трехмерном пространстве
Теперь несколько слов о том, что представляет собой прямая в трехмерном пространстве. Исходя из основного понятия прямой, это некая бесконечная линия, проведенная через точку или две, не считая множества точек, расположенных в последовательности, не изменяющей прямое прохождение линии через них.
Если посмотреть на прямую, проведенную через две точки в трехмерном пространстве, придется учитывать по три координаты обеих точек. То же самое относится к отрезкам и векторам. Последние определяют базис трехмерного пространства и его размерность.
Видео:Координаты вектора. 9 класс.Скачать

Определение векторов и базиса трехмерного пространства
Как принято считать, в трехмерной системе координат может существовать три основных вектора, которые определяют базис. При этом базисов с соответствующими независимыми тремя векторами может быть бесчисленное множество.
Заметьте, это могут быть только три вектора, но вот троек векторов можно определить сколько угодно. Размерность пространства определяется количеством линейно-независимых векторов (в нашем случае – три). И пространство, в котором имеется конечное число таких векторов, называется конечномерным.
Видео:Геометрия 9 класс (Урок№8 - Связь между координатами вектора и координатами его начала и конца.)Скачать

Зависимые и независимые векторы
Что касается определения зависимых и независимых векторов, линейно-независимыми принято считать векторы, являющиеся проекциями (например, векторы оси X, спроецированные на ось Y).
Как уже понятно, любой четвертый вектор является зависимым (теория линейных пространств). А вот три независимых вектора в трехмерном пространстве в обязательном порядке не должны лежать в одной плоскости. Кроме того, если определять независимые векторы в трехмерном пространстве, они не могут являться, так сказать, один продолжением другого. Как уже понятно, в рассматриваемом нами случае с тремя измерениями, согласно общей теории, можно построить исключительно только тройки линейно-независимых векторов в определенной системе координат (без разницы, какого типа).
Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Плоскость в трехмерном пространстве
Если рассматривать понятие плоскости, не вдаваясь в математические определения, для более простого понимания этого термина, такой объект можно рассматривать исключительно как двумерный. Иными словами, это бесконечная совокупность точек, у которых одна из координат является постоянной (константой).
К примеру, плоскостью можно назвать любое количество точек с разными координатами по осям X и Y, но одинаковыми координатами по оси Z. В любом случае одна из трехмерных координат остается неизменной. Однако это, так сказать, общий случай. В некоторых ситуациях трехмерное пространство может пересекаться плоскостью по всем осям.
Видео:9 класс, 2 урок, Координаты вектораСкачать

Существует ли более трех измерений
Вопрос о том, сколько может существовать измерений, достаточно интересен. Как считается, мы живем не в трехмерном с классической точки зрения пространстве, а в четырехмерном. Кроме известных всем длины, ширины и высоты, такое пространство включает в себя еще и время существования объекта, причем время и пространство между собой взаимосвязаны достаточно сильно. Это доказал еще Эйнштейн в своей теории относительности, хотя это больше относится к физике, нежели к алгебре и геометрии.
Интересен и тот факт, что сегодня ученые уже доказали существование как минимум двенадцати измерений. Конечно, понять, что они собой представляют, сможет далеко не каждый, поскольку это относится скорее к некой абстрактной области, которая находится вне человеческого восприятия мира. Тем не менее факт остается фактом. И не зря же многие антропологи и историки утверждают, что наши пращуры могли иметь некие специфичные развитые органы чувств вроде третьего глаза, которые помогали воспринимать многомерную действительность, а не исключительно трехмерное пространство.
Кстати сказать, сегодня существует достаточно много мнений по поводу того, что экстрасенсорика тоже является одним из проявлений восприятия многомерного мира, и тому можно найти достаточно много подтверждений.
Заметьте, что современными базовыми уравнениями и теоремами описать многомерные пространства, отличающиеся от нашего четырехмерного мира, тоже не всегда представляется возможным. Да и наука в этой области относится скорее к области теорий и предположений, нежели к тому, что можно явно ощутить или, так сказать, потрогать или увидеть воочию. Тем не менее косвенные доказательства существования многомерных миров, в которых может существовать четыре и более измерений, сегодня ни у кого не вызывают сомнений.
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Заключение
В целом же, мы очень кратко рассмотрели основные понятия, относящиеся к трехмерному пространству и базовым определениям. Естественно, существует множество частных случаев, связанных с разными системами координат. К тому же мы постарались особо не лезть в математические дебри для объяснения основных терминов только для того, чтобы вопрос, связанный с ними, был понятен любому школьнику (так сказать, объяснение «на пальцах»).
Тем не менее, думается, даже из таких простых трактовок можно сделать вывод о математическом аспекте всех составляющих, входящих в базовый школьный курс алгебры и геометрии.
Геометрическим представлением вектора является направленный отрезок прямой линии, что показано на рис. 1. У каждого вектора есть два свойства: длина (также называемая модулем или нормой вектора) и направление . Благодаря этому векторы очень удобны для моделирования физических величин, которые характеризуются модулем и направлением. Например, в главе 14 мы реализуем систему частиц. При этом мы будем использовать векторы для моделирования скорости и ускорения наших частиц. С другой стороны, в трехмерной компьютерной графике векторы часто используются только для моделирования направления. Например, нам часто требуется указать направление распространения световых лучей, ориентацию грани или направление камеры, глядящей на трехмерный мир. Векторы обеспечивают удобный механизм задания направления в трехмерном пространстве.
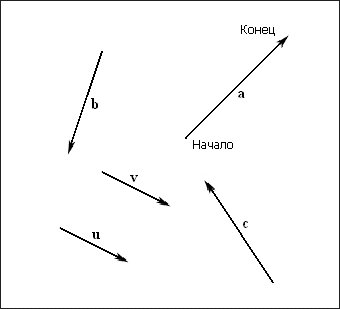 |
Рис. 1. Свободные векторы, определенные независимо от системы координат
Поскольку местоположение не является характеристикой вектора, два вектора с одинаковой длиной и указывающие в одном и том же направлении считаются равными, даже если они расположены в различных местах. Обратите внимание, что два таких вектора будут параллельны друг другу. Например, на рис. 1 векторы u и v равны.
На рис. 1 видно, что обсуждние векторов может вестись без упоминания системы координат, поскольку всю значимую информацию, — длину и направление, — вектор содержит в себе. Добавление системы координат не добавляет информации в вектор; скорее можно говорить, что вектор, значения которого являются его неотъемлимой частью, просто описан относительно конкретной системы координат. И если мы изменим систему координат, мы только опишем тот же самый вектор относительно другой системы.
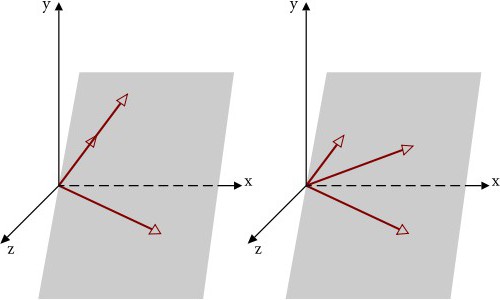
Отметив этот важный момент, мы перейдем к изучению того, как векторы описываются в левосторонней трехмерной декартовой системе координат. На рис. 2 показаны левосторонняя и правосторонняя системы координат. Различие между ними — положительное направление оси Z. В левосторонней системе координат положительное направление оси Z погружается в страницу. В правосторонней системе координат положительное направление оси Z направлено от страницы.
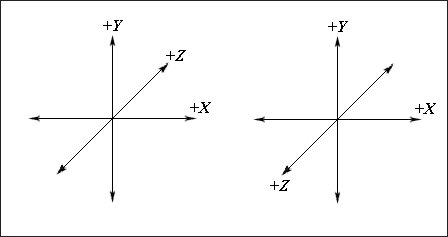 |
Рис. 2. Слева изображена левосторонняя система координат. Обратите внимание, что положительное направление оси Z направлено вглубь страницы. Справа изображена правостороняя система координат. Здесь положительное направление оси Z направлено от страницы
Поскольку местоположение вектора не изменяет его свойств, мы можем перенести векторы таким образом, чтобы начало каждого из них совпадало с началом координат выбранной координатной системы. Когда начало вектора совпадает с началом координат, говорят, что вектор находится в стандартной позиции . Таким образом, если вектор находится в стандартной позиции, мы можем описать его, указав только координаты конечной точки. Мы будем называть эти координаты компонентами вектора. На рис. 3 показаны векторы, изображенные на рис. 1, которые были перемещены в стандартные позиции.
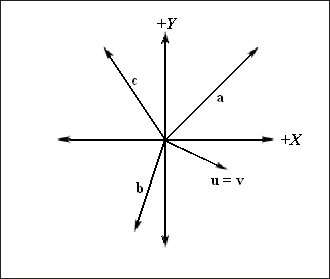 |
Рис. 3. Векторы в стандартной позиции, определенные в указанной системе координат. Обратите внимание, что векторы u и v полностью совпадают друг с другом потому что они равны
Мы будем пользоваться для обозначения векторов полужирными строчными буквами, но иногда будем применять и полужирные заглавные буквы. Вот пример двух-, трех- и четырехмерных векторов соответственно: u = ( u x , u y ), N = ( N x , N y , N z ), c = ( c x , c y , c z , c w ).
Теперь мы введем четыре специальных трехмерных вектора, которые показаны на рис. 4. Первый из них называется нулевым вектором , и значения всех его компонент равны нулю; мы будем обозначать такой вектор выделенным полужирным шрифтом нулем: 0 = (0, 0, 0). Следующие три специальных вектора называются единичными базовыми векторами (базовыми ортами) трехмерной системы координат. Эти векторы, направленные вдоль осей X, Y и Z нашей координатной системы, мы будем называть i , j и k соответственно. Модуль этих векторов равен единице, а определение выглядит следующим образом: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).
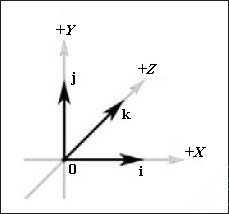 |
Рис. 4. Нулевой вектор и базовые орты трехмерной системы координат
В библиотеке D3DX для представления векторов в трехмерном пространстве мы можем воспользоваться классом D3DXVECTOR3 . Его определение выглядит следующим образом:
Обратите внимание, что D3DXVECTOR3 наследует компоненты от D3DVECTOR , определение которого выглядит следующим образом:
Так же, как и у скалярных величин, у векторов есть собственная арифметика, что видно из наличия описаний математических операций в определении класса D3DXVECTOR3. Возможно, сейчас вы не знаете, что делают эти методы. В следующих подразделах мы рассмотрим эти операции с векторами, другие вспомогательные функции работы с векторами из библиотеки D3DX и некоторые важные особенности обработки векторов.
Равенство векторов
В геометрии два вектора считаются равными, если они указывают в одном и том же направлении и имеют одинаковую длину. В алгебре говорят, что векторы равны, если у них одинаковое количество измерений и их соответствующие компоненты равны. Например, ( u x , u y , u z ) = ( v x , v y , v z ) если u x = v x , u y = v y и u z = v z .
В коде мы можем проверить равны ли два вектора, используя перегруженный оператор равенства:
Аналогичным образом, можно убедиться, что два вектора не равны, используя перегруженный оператор неравенства:
Вычисление модуля вектора
В геометрии модулем вектора называется длина направленного отрезка линии. В алгебре, зная компоненты вектора мы можем вычислить его модуль по следующей формуле:
Вертикальные линии в |u| обозначают модуль u .
| ПРИМЕР |
Вычислите модуль векторов u = (1, 2, 3) и v = (1, 1).
Решение
Для вектора u мы получаем:
Обобщив формулу (1) для двухмерного пространства, для вектора v мы получим:
Работая с библиотекой D3DX, для вычисления модуля вектора мы можем применять следующую функцию:
Нормализация вектора
В результате нормализации получается вектор, направление которого совпадает с исходным, а модуль равен единице (единичный вектор). Чтобы нормализовать произвольный вектор, достаточно разделить каждый компонент вектора на модуль вектора, как показано ниже:
Мы отмечаем единичный вектор, помещая над его обозначением символ ^ : û .
| ПРИМЕР |
Нормализуйте векторы u = (1, 2, 3) и v = (1, 1).
Решение
Из приведенных выше формул (2) и (3) мы знаем, что |u| = √ 14 и |v| = √ 2 , поэтому:
В библиотеке D3DX для нормализации векторов применяется следующая функция:
Сложение векторов
Мы можем сложить два вектора, сложив их соответствующие компоненты; обратите внимание, что размерность складываемых векторов должна быть одинаковой:
Геометрическая интерпретация сложения векторов показана на рис. 5.
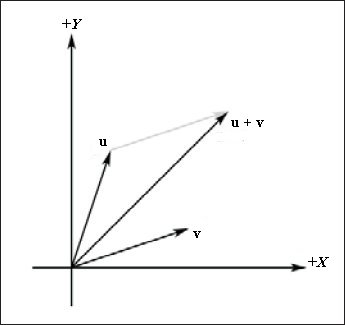 |
Рис. 5. Сложение векторов. Обратите внимание, как мы выполняем параллельный перенос вектора v таким образом, чтобы его начало совпало с концом вектора u ; суммой будет вектор начало которого совпадает с началом вектора u , а конец совпадает с концом перенесенного вектора v
В коде для сложения двух векторов мы будем применять перегруженый оператор сложения:
Вычитание векторов
Аналогично сложению, вычитание векторов осуществляется путем вычитания их отдельных компонент. Опять же оба вектора должны иметь одинаковую размерность.
Геометрическая интерпретация вычитания векторов показана на рис. 6.
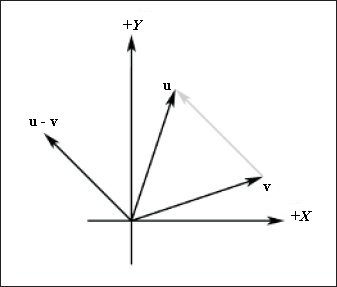 |
Рис. 6. Вычитание векторов
В коде для вычитания двух векторов мы будем применять перегруженый оператор вычитания:
Как видно на рис. 6, операция вычитания векторов возвращает вектор, начало которого совпадает с концом вектора v , а конец — с концом вектора u . Если мы интерпретируем компоненты u и v как координаты точек, то результатом вычитания будет вектор, направленный от одной точки к другой. Это очень удобная операция, поскольку нам часто будет необходимо найти вектор, описывающий направление от одной точки к другой.
Умножение вектора на скаляр
Как видно из названия раздела, мы можем умножать вектор на скаляр, в результате чего происходит масштабирование вектора. Если масштабный множитель положителен, направление вектора не меняется. Если же множитель отрицателен, то направление вектора изменяется на противоположное (инвертируется).
Класс D3DXVECTOR3 предоставляет оператор умножения вектора на скаляр:
Скалярное произведение векторов
Скалярное произведение векторов — это первая из двух определенных в векторной алгебре операций умножения. Вычисляется такое произведение следующим образом:
У приведенной выше формулы нет очевидной геометрической интерпретации. Используя теорему косинусов 1 , мы получим отношение u Ч v = |u||v| cos j , говорящее, что скалярное произведение двух векторов равно произведению косинуса угла между векторами на модули векторов. Следовательно, если u и v — единичные векторы, их скалярное произведение равно косинусу угла между ними.
Вот некоторые полезные свойства скалярного произведения:
- Если u Ч v = 0, значит u ^ v .
- Если u Ч v > 0, значит угол j между двумя векторами меньше 90 градусов.
- Если u Ч v j между двумя векторами больше 90 градусов.
Для вычисления скалярного произведения двух векторов в библиотеке D3DX предназначена следующая функция:
Векторное произведение
Второй формой операции умножения, определенной в векторной алгебре, является векторное произведение. В отличие от скалярного произведения, результатом которого является число, результатом векторного произведения будет вектор. Векторным произведением двух векторов u и v будет другой вектор, p , являющийся взаимно перпендикулярным для векторов u и v . Это означает, что вектор p перпендикулярен вектору u и одновременно вектор p перпендикулярен вектору v .
Вычисляется векторное произведение по следующей формуле:
В компонентной форме вычисление выглядит так:
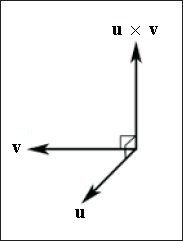 |
Рис. 7. Векторное произведение. Вектор p = u × v перпендикулярен как вектору u, так и вектору v
| ПРИМЕР |