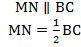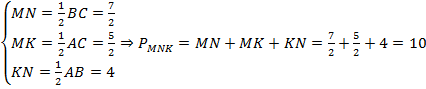Как найти длину линии треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Найди длину средней линии | Подготовка к ОГЭСкачать

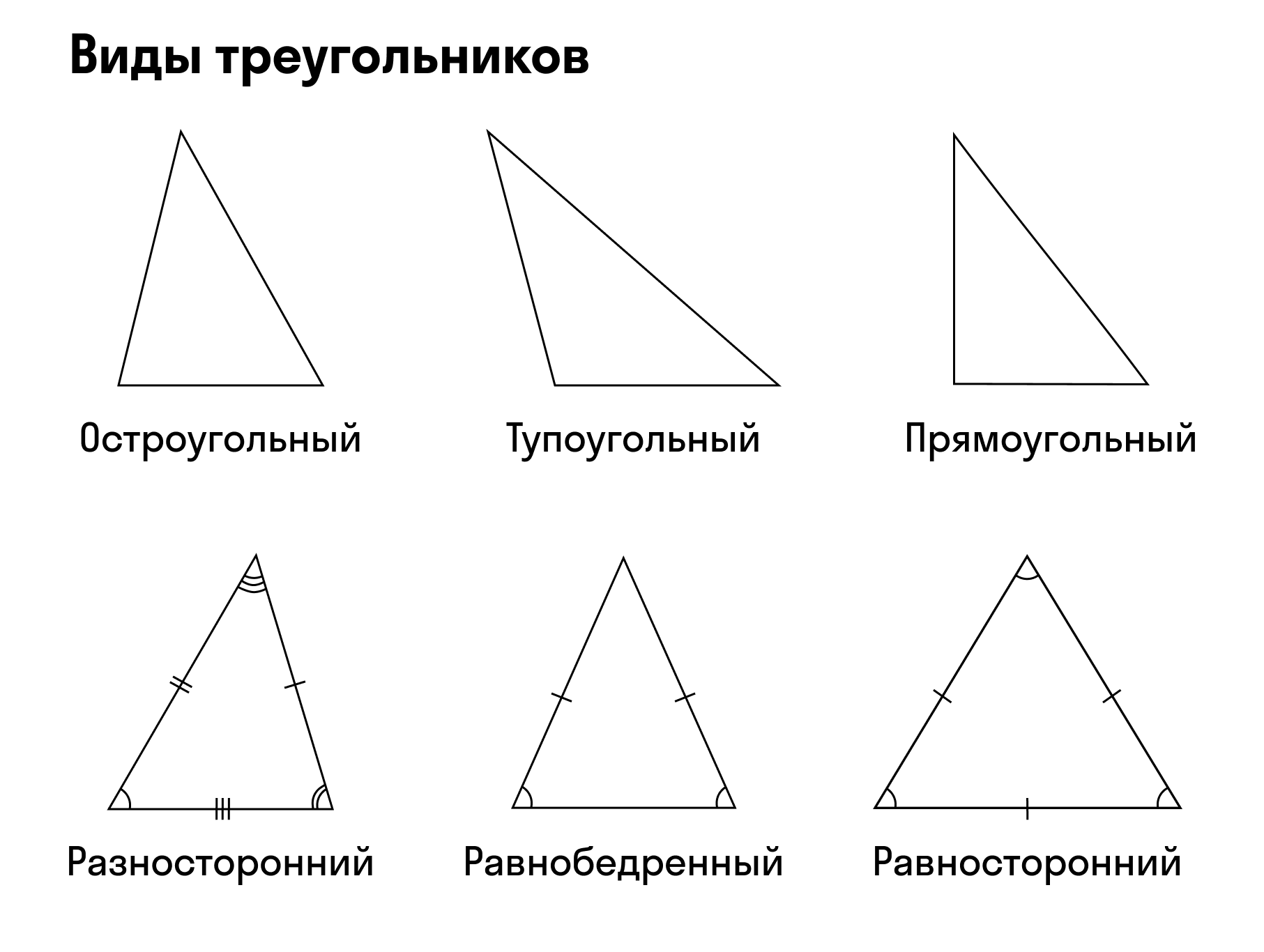
Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

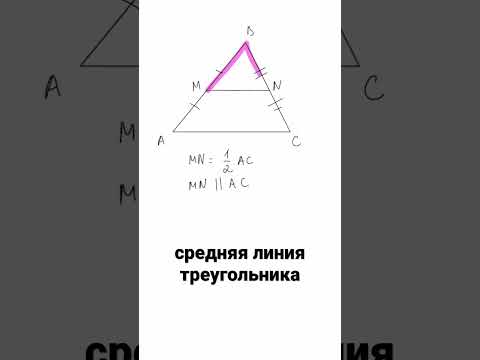
​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Видео:Средняя линия треугольникаСкачать

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Видео:МАТЕМАТИКА | Средняя линия треугольникаСкачать

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

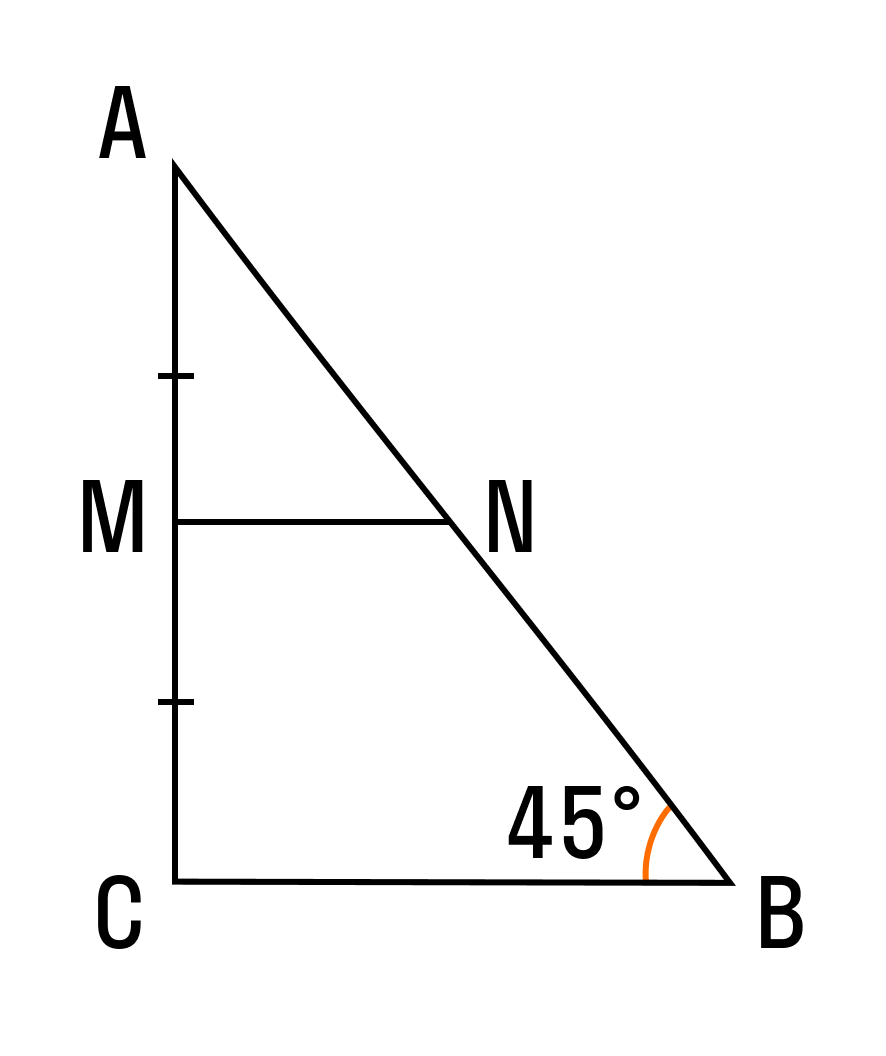
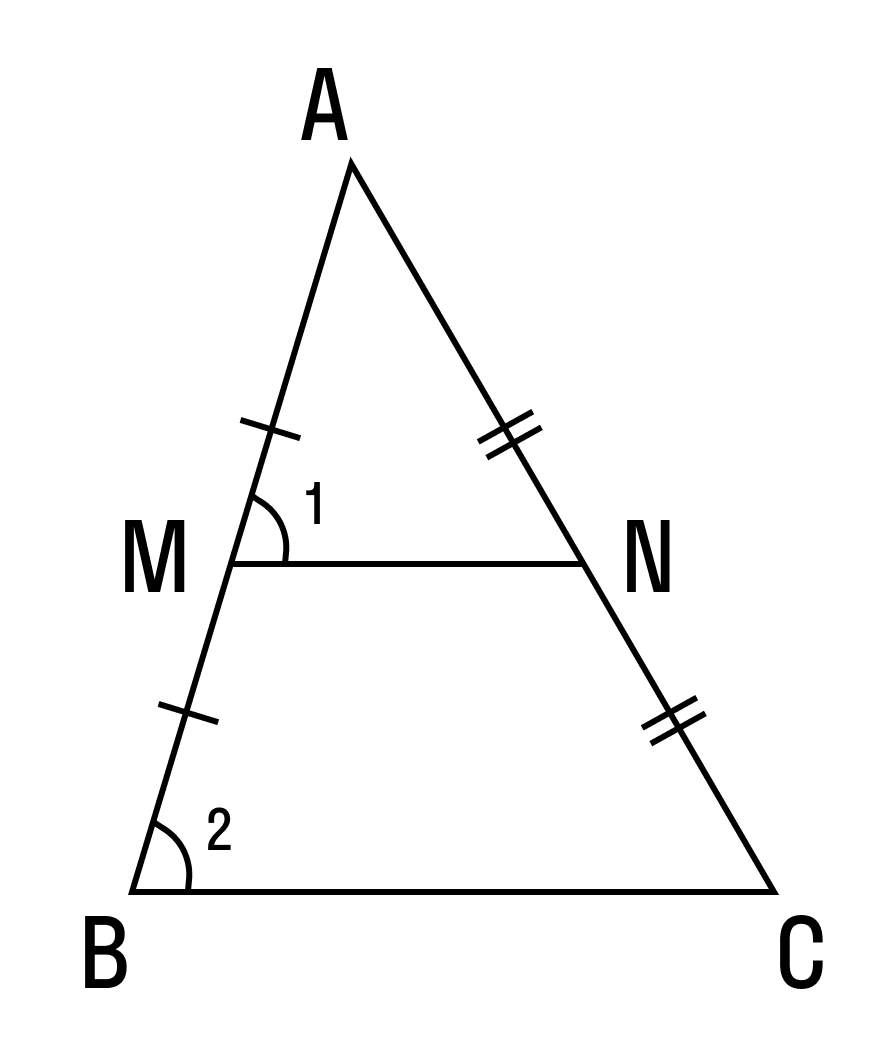
Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.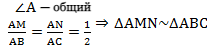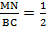

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

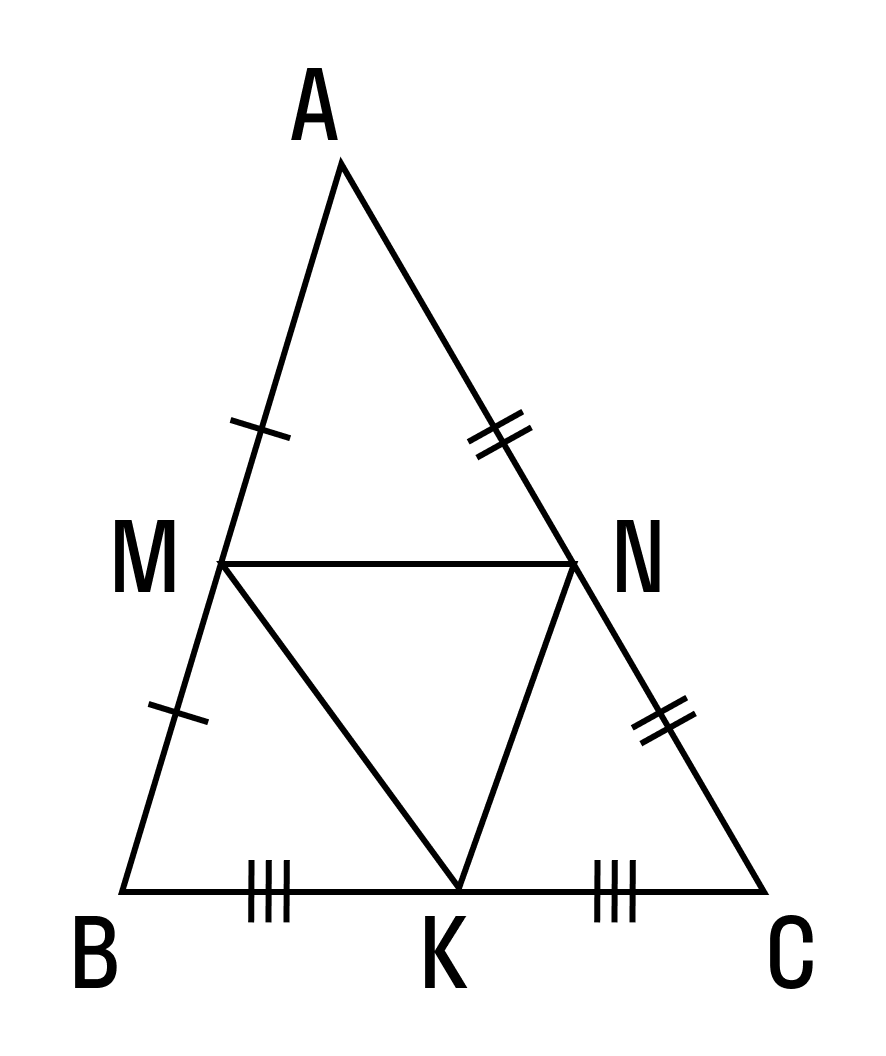
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Длина средней линии треугольника – формула

Средняя линия треугольника интересный характеризующий отрезок, так как обладает несколькими свойствами, позволяющими найти простое решение для казалось бы сложной задачи. Поэтому рассмотрим основные свойства средней линии и поговорим о том, как найти длину этого отрезка в треугольнике.

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

Треугольник и его характеризующие отрезки

Треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от углов треугольники делятся на:

• Остроугольные
• Тупоугольные
• Прямоугольные

Рис. 1. Виды треугольников

Основными характеризующими отрезками треугольника являются:

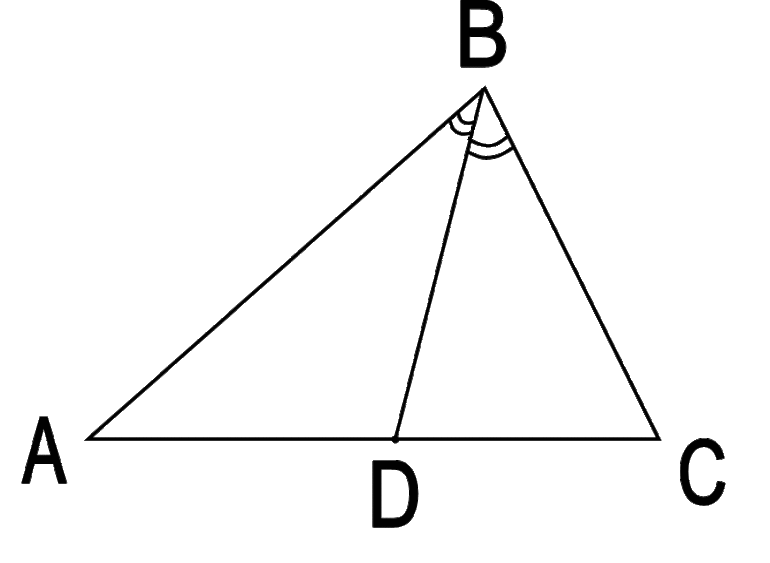
• Медиана – отрезок, соединяющий вершину с серединой противоположной стороны.
• Биссектриса – отрезок, делящий угол пополам
• Высота – перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Рис. 2. Высота, медиана и биссектриса в треугольнике

Для каждого из характеризующих отрезков существует своя точка пересечения. При соединении трех точек пересечения медиан, биссектрис и высот получается золотое сечение треугольника.

Однако существует и ряд дополнительных характеризующих отрезков:

• Серединный перпендикуляр – высота восстановленная из середины высоты. Как правило серединный перпендикуляр продолжается до пересечения с другой стороной.
• Средняя линия – отрезок, соединяющий середины смежных сторон.
• Радиус вписанной окружности. Вписанная окружность – окружность, которая касается каждой из сторон треугольника.
• Радиус описанной окружности. Описанная окружность – окружность, содержащая в себе все стороны треугольника.

Смежными сторонами треугольников называют стороны, которые имеют общую вершину. В геометрии существует понятие противоположных сторон, т.е. сторон, которые лежат друг напротив друга и не имеют общих вершин. Но это понятие для треугольников не применимо – любая пара сторон в треугольнике является смежной.

Видео:СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать

Свойство средней линии

Свойств средней линии не так много, но все они имеют значение при решении задач. Дело в том, что задач на нахождение длины средней линии мало, а потому некоторые из них способны построить ученика в ступор при всей своей простоте.

Поэтому приведем и обсудим все свойства средней линии треугольника:

• Средняя линия равна половине основания. Вообще правильнее сказать не половине основания, а половине противолежащей стороны. Так как сторон в треугольнике 3, а основание всего одно. Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить. В общем случае по этому свойству и определяется длина средней линии треугольника.
• Средняя линия параллельна основанию. С понятием основания здесь та же ситуация, что и в прошлом свойстве.
• Средняя линия отсекает от треугольника малый подобный треугольник с коэффициентом подобия, равным 0,5
• Три средние линии делят треугольник на 4 равных треугольника, подобных большому треугольнику с коэффициентом подобия 0,5

Рис. 3. Средние линии в треугольнике

Собственно формула длины средней линии вытекает из второго свойства:

$m=1over*a$- где m – средняя линия, а- сторона противоположная средней линии.

Видео:СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА 8 класс Атанасян геометрияСкачать

Что мы узнали?

Мы поговорили о второстепенных характеризующих отрезках, выделив среднюю линию. Привели свойства средних линий и поговорили о особенностях формулировки этих свойств. Рассказали, как выводится формула длины средней линии треугольника и как средняя линия разбивает треугольник. Все эти свойства используются при решении треугольников.

Видео:Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

Длина средней линии треугольника — формула, признаки подобия и свойства

Видео:64. Средняя линия треугольникаСкачать

Фигура с тремя вершинами

Прежде чем понять, как найти ср. линию треугольника, необходимо рассмотреть фигуру, о которой пойдет речь. Каждый человек, даже плохо знакомый с геометрией, все же отчетливо представляет объект на плоскости, состоящий из трех вершин и трех сторон. Каждая вершина соединяется с двумя другими прямыми отрезками. Они называются сторонами.

Существующие типы

Рассматриваемый геометрический объект бывает нескольких типов. Наиболее известные из них следующие:

• равносторонний, у которого все стороны и углы равны между собой;
• равнобедренный, который имеет лишь две равные по длине стороны и отличающуюся от них третью;
• прямоугольный, у которого один из трех углов составляет 90 градусов, то есть является прямым.

Одним из важных свойств рассматриваемой фигуры произвольного типа является равенство 180 градусам суммы его трех углов. Именно по этой причине фигура может иметь либо три острых угла, либо один тупой и два меньше 90 градусов. Два прямых угла он также не может иметь, поскольку третья вершина должна будет лежать в бесконечности, чтобы иметь нулевой угол (90 + 90 + 0 = 180).

Основные геометрические элементы

К ним относятся типичные для треугольника отрезки, которые обладают определенными характеристиками. Наиболее известны из них следующие:

1. Медиана. Она опускается из любой из трех вершин на середину противоположной стороны. Медиана делит треугольник на две равные по площади части, а точка пересечения трех подобных отрезков является геометрическим и гравитационным центром фигуры.
2. Биссектриса. Этот отрезок делит пополам угол вершины, из которой он проведен.
3. Высота. Она представляет собой перпендикулярный к противоположной стороне отрезок, опущенный из любой вершины треугольника. Высота делит фигуру на два прямоугольных геометрических объекта, сама является общей для них стороной и катетом.
4. Средняя линия. Это отрезок, который соединяет любые две точки треугольника, лежащие на серединах его сторон. В рассматриваемой фигуре можно провести три различных таких линии.

В общем случае первые три линейных элемента из списка не совпадают друг с другом, однако для определенных типов треугольников они могут быть одинаковыми. Например, для равносторонней фигуры не существует разницы между биссектрисами, медианами и высотами.

В случае треугольника равнобедренного лишь биссектриса, выходящая из вершины, образованной одинаковыми сторонами, также является медианой и высотой одновременно.

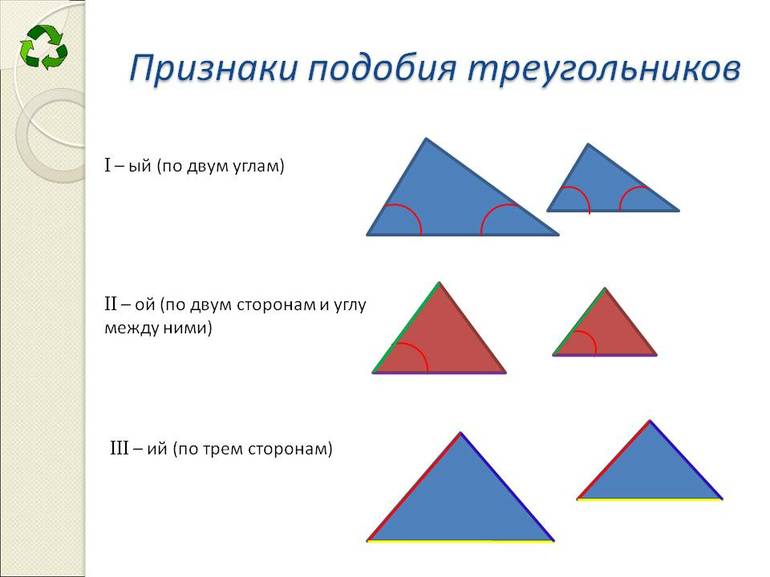
Признаки подобия

Важно рассмотреть признаки подобия треугольников, чтобы понимать все свойства, связанные со средним отрезком фигуры. Подобными являются геометрические объекты, которые имеют полностью идентичную форму, но разный размер. Например, два любых квадрата всегда подобны друг другу, поскольку один из них является увеличенной/уменьшенной копией другого.

Применительно к треугольникам существуют следующие признаки их подобия:

1. Равенство любых двух углов. Поскольку сумма трех углов является величиной постоянной, то этот признак свидетельствует о факте равенства всех трех рассматриваемых элементов.
2. Одинаковое соотношение всех трех сторон. Например, даны треугольники ABC и A1B1C1, для которых справедливо равенство: AB/A1B1 = BC/B1C1 = AC/A1C1 = k. Это означает, что обе фигуры подобны друг другу, при этом коэффициент их подобия равен k.
3. Существует коэффициент подобия для двух любых сторон рассматриваемых треугольников, а угол между ними является одинаковым. Математически это записывается так: A = A1 и AB/A1B1=AC/A1C1 = k.

Любой из этих признаков является достаточным, чтобы подтвердить подобие двух изучаемых треугольников. При доказательстве свойств среднего отрезка используют отмеченные признаки.

Видео:Определение длины средней линии треугольникаСкачать

Средняя линия

Чтобы понять, как найти середину треугольника, можно воспользоваться обычной линейкой. Для этого необходимо выбрать произвольные две стороны фигуры. Затем отметить на каждой из них точки, отстоящие на одинаковом расстоянии от соответствующих вершин, которые ограничивают данную сторону. Полученные две точки следует соединить, чтобы начертить средний отрезок. Его название является интуитивно понятным каждому, поскольку он соединяет середины двух сторон.

Важные свойства

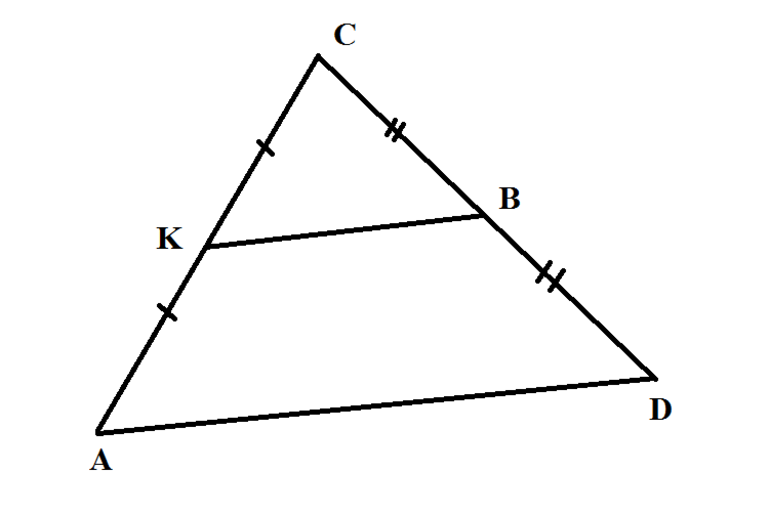
Существует три основных свойства, которыми обладает рассматриваемый отрезок. Пусть имеется треугольник произвольного типа ABC, в котором точки P и Q лежат на серединах сторон AB и AC соответственно. При таком обозначении отрезок PQ будет средней линией треугольника ABC. Справедливы следующие геометрические свойства:

1. Полученный треугольник APQ является подобным исходной фигуре ABC. Доказать это утверждение несложно, если обратить внимание на два факта: во-первых, угол A у обеих фигур является общим, во-вторых, отношение AB/AP равно величине AC/AQ и составляет 2 согласно выполненным геометрическим построениям. Таким образом, выполняется один из признаков подобия.
2. Длина средней линии PQ оказывается в два раза меньше, чем сторона BC. Кроме того, оба отрезка параллельны друг другу. Утверждение о равенстве PQ = ½*BC следует из факта подобия треугольников APQ и ABC, коэффициент которых составляет 2. Это равенство также можно доказать, если воспользоваться координатным методом.
3. Треугольник APQ имеет в 4 раза меньшую площадь, чем исходная фигура ABC.

Утверждение № 3 из списка справедливо для произвольного треугольника. Для его доказательства следует воспользоваться формулой Герона. Согласно ей, площадь рассматриваемой фигуры может быть вычислена следующим образом:

Здесь p = (a+b+c)/2 — полупериметр фигуры. Буквами a, b и c обозначены длины ее сторон. Пусть таким же образом обозначаются стороны для треугольника ABC. Тогда для фигуры APQ они будут иметь длины a/2, b/2 и c/2. Полупериметр для APQ составит величину p1 = (a+b+c)/4 = ½*p. Теперь необходимо подставить все известные величины в формулу Герона, получается площадь S1:

Иными словами, площадь треугольника APQ составляет четвертую часть от этой величины для ABC.

Решение задачи

В треугольнике ABC проведен средний отрезок PQ, граничные точки которой P и Q находятся на сторонах AB и AC соответственно. Необходимо с использованием метода координат доказать, что эта линия имеет в два раза меньшую длину, чем сторона BC.

Прежде чем находить решение этой задачи, следует обозначить координаты вершин исходной фигуры. Они будут следующие:

Поскольку точка P делит ровно пополам сторону AB, то для нахождения ее координат необходимо провести следующие вычисления:

Аналогичным образом рассчитываются координаты точки Q:

Вспоминая формулу для длины вектора, координаты конца и начала которого известны, для средней линии PQ можно произвести следующие вычисления:

PQ = (((x1+x3)/2 — (x1+x2)/2)^2 + ((y1+y3)/2 — (y1+y2)/2)^2)^0,5 = ½*((x3-x2)^2 + (y3-y2)^2)^0,5.

В свою очередь, длина стороны BC равна:

BC = ((x3-x2)^2 + (y3-y2)^2)^0,5.

Из сопоставления этих двух равенств следует искомая формула, которую требовалось доказать:

Поскольку в процессе доказательства были использованы произвольные координаты для вершин треугольника, полученный вывод является общим и универсальным для любого типа рассматриваемых фигур.

Видео:Средняя линия треугольника. Видеоурок 13. Геометрия 8 класс.Скачать

Срединный треугольник

Это особый вид фигуры с тремя вершинами, который строится на средних линиях. Поскольку любой треугольник имеет всего три линии указанного вида, то вместе они образуют новую фигуру, вершины которой расположены на серединах сторон исходной.

Построенный геометрический объект делит исходную фигуру на четыре одинаковые части. Доказать это можно следующим образом: если начертить срединный треугольник и обозначить черточками все его стороны, а также длины сторон исходного геометрического объекта, то можно увидеть, что сам он, а также три других фигуры при вершинах исходной имеют по три одинаковых стороны. Иными словами, выполняется признак их подобия. Равенство сторон всех четырех фигур говорит об одинаковом значении их площадей.

Еще одним интересным свойством срединной фигуры является возможность построения внутри нее точно такого же геометрического объекта. Он также будет подобен исходному треугольнику, но уже будет иметь в 8 раз меньшую площадь. Если продолжать такие геометрические построения, то площади срединных треугольников будут становиться все меньше, а пространство на плоскости, которое они будут покрывать, стремится к гравитационному центру исходной фигуры.

Таким образом, формула длины средней линии получается исходя из признака подобия треугольников по углу и двум прилежащим сторонам. Она всегда составляет половину от противоположной стороны. При выполнении геометрического построения срединного треугольника образуются четыре новых фигуры, которые подобны исходной. Гравитационные центры первоначального геометрического объекта и срединной фигуры совпадают.

🔥 Видео

Средняя линия треугольникаСкачать

Лайфхаки ОГЭ — средняя линия треугольникаСкачать

Теорема о средней линии треугольникаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Средняя линия треугольника – 8 класс геометрияСкачать

ОГЭ ЗАДАНИЕ 18 НАЙТИ ДЛИНУ СРЕДНЕЙ ЛИНИИ ТРАПЕЦИИСкачать

Геометрия 8. Средняя линия трапеции. Средняя линия треугольника. Задачи.Скачать