Как найти отношение двух векторов (5 видео)

найти отношение двух векторов по коэффициенту детерминации

У меня есть вопрос о коэффициенте детерминации.

Мне нужно найти отношения двух векторов.

Учитывая два числовых вектора x и y, их определение коэффициента может быть выражено как:

Я получил формулу из некоторого кода, но я не знаю авторов.

Любая помощь будет оценена!

Содержание

Решение
Отношение коллинеарных векторов
Свойства отношений коллинеарных векторов
Операции над векторами и их свойства: сложение и умножение
Сложение двух векторов
Сложение нескольких векторов
Умножение вектора на число
Свойства операций над векторами
🔍 Видео

Видео:6 класс, 20 урок, ОтношенияСкачать

Решение

В статистике коэффициент детерминации, обозначаемый как R2 и произносится как R в квадрате, показывает, насколько хорошо точки данных соответствуют статистической модели — иногда просто линия или кривая. Это статистика, используемая в контексте статистических моделей, основной целью которых является либо прогнозирование будущих результатов, либо проверка гипотез на основе другой связанной информации. Он обеспечивает меру того, насколько хорошо наблюдаемые результаты воспроизводятся моделью, как доля общего изменения результатов, объясненная моделью. [1
Коэффициент корреляции, r , и коэффициент детерминации, r^2 .

Математическая формула для вычислений r является:

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Отношение коллинеарных векторов

В данном разделе рассматриваются векторы, коллинеарные заданной прямой , т.е. принадлежащие или параллельные ей.

Согласно определению (см. разд. 1.1.2), при умножении данного вектора на число получаем вектор, коллинеарныи данному. Можно определить и «обратную» операцию — «деление коллинеарных векторов».

Отношением коллинеарных векторов и называется действительное число, равное по модулю отношению длин этих векторов, положительное, если векторы и одинаково направленные, и отрицательное, если векторы и противоположно направленные:

По определению равенство эквивалентно равенству для любых коллинеарных векторов и .

Например, найдем отношения коллинеарных векторов, изображенных на рис. 1.6:

Видео:Отношение двух чисел. 6 класс.Скачать

Свойства отношений коллинеарных векторов

Для любых коллинеарных векторов справедливы следующие свойства:

1. Отношение любых коллинеарных векторов и определено однозначно.

2. Арифметические действия с отношениями коллинеарных векторов аналогичны действиям с числовыми дробями, а именно для любых коллинеарных векторов справедливы равенства

Докажем первое свойство. Предположим противное. Пусть и , причем . Тогда и , т.е. , и следовательно, . Разделив обе части равенства на число , получим , что противоречит условию .

Докажем, например, последнее равенство (свойство 2,г). Пусть и , тогда и . Надо доказать, что . Найдем отношение длин векторов . По определению получаем , где знак плюс берется, если , а минус — при .

Если все векторы одинаково направлены, то 0,

mu>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAG4AAAAUBAMAAACezBVvAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAgRC9nkHpYdAhCzFRcXBTpToAAAGMSURBVDjLY2AgF7CaKGCIbVXAp4MpEkydc0CXUDZsxKdPTNgIRLE9QpcwZlArwK2NJ5PBA0TzPgdzWQLgLn/KwJKArroW7nQ2A4a4A0Ca8zGYy+kMs4PlNQPjS3R97I0wjfMEGPTAXrObAPGuBFQj8wMGxqcw9ZMnMJyBaGyBKGOIE2DgMwAx6i5Aw0niElzfQ5g+uQkMKbCAh2iUg+mb1wAL4BtCGPrMGFifw/xtHADT9wCkuu013BcVQuj6niD5ldV5A1QfKNg0ap4g9DlB9cHteM7ADA9bTrC+cxB3cqcwpKFYx8DyFBEuQMv4HFDduU+AYR5Q3zYHBr8D0HARgoQcOP5CYWF0rtIAGi4b4PFXwMCdocCwzwGirQhqcAqDmgDTO7AqvkdMfbEFKPHAmMTgpsDA3MTAwJEEcrwHPG1tc29RYGoTAEdWsnCYMYo2BgaPkmygcmAyYAoC+eoAIsGfBdrFA45VuZkbGMC+KkRkEe47+LILywZI9JEKNkOjj1QgCY0+8kAADnEA9wdbw8+fGPAAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, поэтому .

Если и , то и , так как .

Таким образом, во всех случаях получаем , что и требовалось доказать.

Пример 1.4. Диагонали трапеции высекают на её средней линии отрезок (рис. 1.12). Найти отношения векторов

Решение. По свойствам средних линий треугольника и трапеции находим отношения коллинеарных векторов:

Отсюда следуют соотношения

Теперь, используя свойства отношений коллинеарных векторов, получаем

Видео:Скалярное произведение векторов. 9 класс.Скачать

Операции над векторами и их свойства: сложение и умножение

Прежде чем приступить к тематике статьи, напомним основные понятия.

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

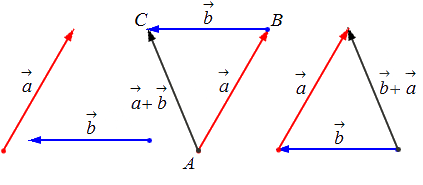
Сложение двух векторов

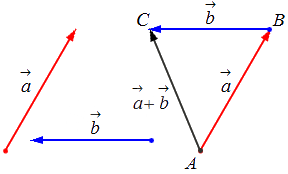
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

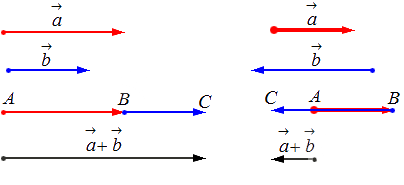
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Видео:Процентное отношение двух чисел. 6 класс.Скачать

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

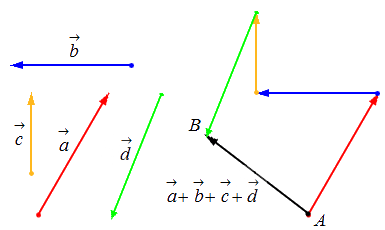
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .

Видео:Отношение двух чисел. Практическая часть - решение задачи. 1 часть. 6 класс.Скачать

Умножение вектора на число

Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

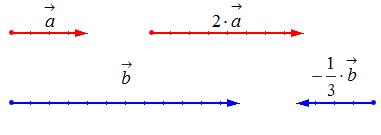
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Видео:Отношение двух чисел. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .

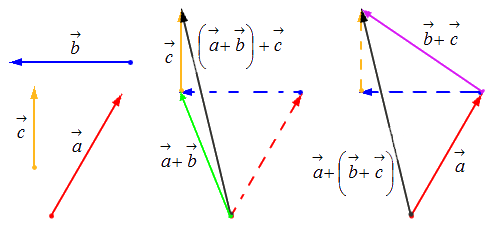
Свойство коммутативности: a ⇀ + b → = b → + a → .
Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
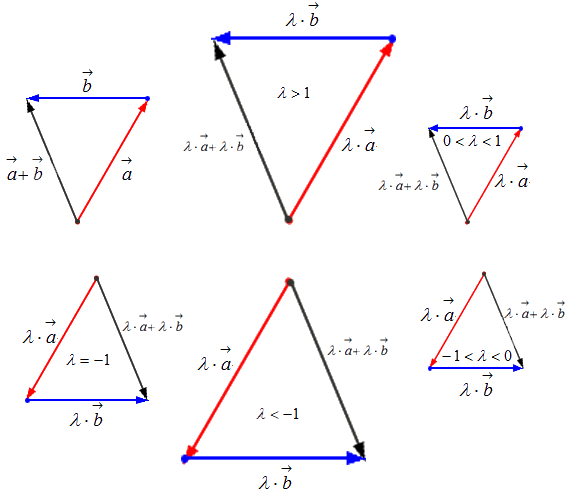
Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →