Как найти координаты вектора в базисе abc (5 видео)

Как найти координаты вектора в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a, b, c и d . Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»₁, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

A =

4	3	5
6	7	1
9	1	8

B =

-1	3	-2
-4	1	2
3	-4	5

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

A -1 = -1/182

55	-19	-32
-39	-13	26
-57	23	10

Матрицу Х ищем по формуле:

X = A -1 ·B = -1/182

55	-19	-32
-39	-13	26
-57	23	10

-1	3	-2
-4	1	2
3	-4	5

75 /₁₈₂	-1 46 /₉₁	1 9 /₁₃
-13 /₁₄	1 2 /₇	-1
5 /₁₈₂	1 3 /₉₁	-1 2 /₁₃

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Содержание

Математический портал
Nav view search
Navigation
Search
Базис линейного пространства. Разложение вектора по базису.
Онлайн калькулятор. Разложение вектора по базису.
Калькулятор для разложения вектора по базисным векторам
Инструкция использования калькулятора для разложение вектора по базисным векторам
Ввод данных в калькулятор для разложение вектора по базисным векторам
Дополнительные возможности калькулятора разложение вектора по базисным векторам
Теория. Разложение вектора по базису
🔥 Видео

Видео:Найдите разложение вектора по векторам (базису)Скачать

Математический портал

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Nav view search

Search

Вы здесь:
Home

Видео:Как разложить вектор по базису - bezbotvyСкачать

Базис линейного пространства. Разложение вектора по базису.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Упорядоченная тройка некомпланарных векторов $e_1, e_2, e_3$ называется базисом в пространстве всех геометрических векторов. Всякий геометрический вектор $a$ может быть представлен единственным образом в виде $$a=X_1e_1+X_2e_2+X_3e_3.qquadqquadqquadqquadqquad (1)$$ Числа $X_1, X_2, X_3$ называются координатами вектора в базисе $B=.$ Запись (1) называют разложением вектора $a$ по базису $B.$

Аналогично, упорядоченная пара неколлинеарных векторов $e_1, e_2$ называется базисом $B=(e_1, e_2)$ в множестве геометрических векторов, компланарных некоторой плоскости.

Наконец, всякий ненулевой вектор $e$ образует базис $B=(e)$ в множестве геометрических векторов, коллинеарных некоторому направлению.

Если вектор $a$ есть линейная комбинация векторов $a_1, a_2, . a_n$ с коэффициентами $lambda_1, lambda_2, . lambda_n$, то есть $$a=sumlimits_^n lambda_ka_k$$ то каждая координата $X_i(a)$ вектора $a$ равна сумме произведений коэффициентов $lambda_1,lambda_2. lambda_n$ на одноименные координаты векторов $a_1, a_2, . a_n: $ $$X_i(a)=sumlimits_^nlambda_k X_i(a_k),qquad (i=1, 2, 3.)$$

Базис $B=(e_1, e_2, e_3)$ называется прямоугольным, если векторы $e_1, e_2$ и $e_3$ попрано перпендикулярны и имеют единичную длину. В этом случае приняты обозначения $$e_1=i;,, e_2-j;,, e_3=k.$$

Примеры.

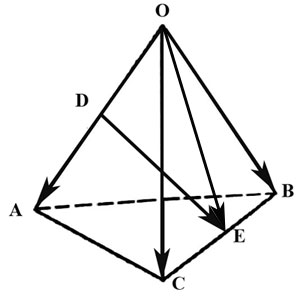
2.26. Задан тетраэдр $OABC.$ В базисе из ребер $overline, overline$ и $overline$ найти координаты:

а) вектора $overline,$ где $D$ и $E$ середины ребер $OA$ и $BC.$

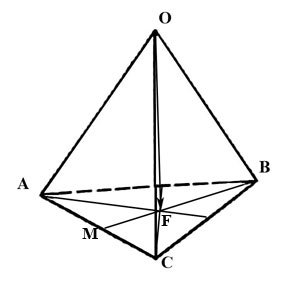
б) вектора $overline,$ где $F-$ точка пересечения медиан основания $ABC.$

Решение.

а)

Выразим вектор $overline$ через вектора $overline, overline, overline:$

Из треугольника $ODE$ имеем $overline=overline+overline.qquadqquadqquad (1)$

вектор $overline$ найдем из треугольника $OBE:$

здесь $overline=fracoverline,$ а вектор $overline$ находим из треугольника $OBC:$

Таким образом, из (2) получаем $overline=overline+frac(overline-overline).$

Наконец из (1) имеем $$overline=overline+overline=-fracoverline+overline+frac(overline-overline)=$$ $$=-fracoverline+fracoverline+fracoverline.$$

Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(-frac,frac,fracright).$

Ответ: $left(-frac; frac; fracright).$

б)

Выразим вектор $overline$ через вектора $overline, overline, overline:$

Из треугольника $OFB$ имеем $overline=overline+overline.qquadqquadqquad (1)$

вектор $overline$ найдем из треугольника $BMC:$

здесь $overline=fracoverline,$ а вектор $overline$ находим из треугольника $OCA:$

Таким образом, из (2) получаем $$overline=overline+overline=overline-overline+fracoverline=$$ $$=overline-overline+frac(-overline+overline).$$

Наконец из (1) имеем $$overline=overline+overline=overline+fracoverline=$$ $$=overline+fracleft(overline-overline+frac(-overline+overline)right)=$$ $$=overline+fracoverline-fracoverline+frac(-overline+overline)=fracoverline+fracoverline+fracoverline.$$

Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(frac; frac; fracright).$

Ответ: $left(frac; frac; fracright).$

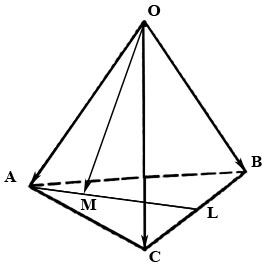
2.27. В тетраэдре $OABC$ медиана $AL$ грани $ABC$ делится точкой $M$ в отношении $|overline|:|overline|=3:7.$ Найти координаты вектора $overline$ в базисе из ребер $overline, overline, overline.$

Решение.

Вектор $overline$ найдем из треугольника $AOM:$ $$overline=overline+overline.qquadqquadqquad (1)$$

Из условия $|overline|:|overline|=3:7$ имеем $overline=fracoverline.$ Из треугольника $ABL$ находим $overline=overline+overline=overline+fracoverline.$

Далее, из треугольников $AOB$ и $BOC$ получаем

Отсюда и из (1) получаем $$overline=overline+overline=overline+fracoverline+fracoverline+fracoverline=$$ $$=fracoverline-fracoverline+fracoverline.$$

Ответ: $left(frac; frac;fracright).$

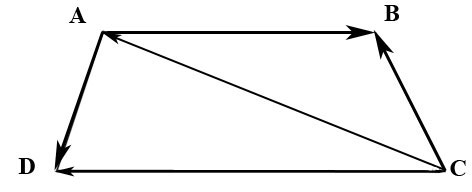
2.29. В трапеции $ABCD$ известно отношение длин оснований $|overline|/|overline|=lambda$ Найти координаты вектора $overline$ в базисе из векторов $overline$ и $overline.$

Решение.

Вектор $overline$ можно найти из треугольника $ABC:$ $overline=overline+overline.$

$overline$ находим из треугольника $ACD:$ $overline=overline+overline=overline-overline.$

Из условия $|overline|/|overline|=lambda$ находим вектор $overline:$ $overline=-overline/lambda.$

Таким образом, $overline=-overline/lambda-overline;$

2.36. Заданы векторы $e(-1, 1, 1/2)$ и $a(2, -2, -1).$ Убедиться, что они коллинеарны и найти разложение вектора $a$ по базису $B(e). $

Решение.

Векторы коллинеарны, если их направления совпадают или противоположны, т.е. тогда и только тогда когда их координаты пропорциональны. Проверим: $$frac=frac=frac=-frac,$$ то есть векторы $e$ и $a$ коллинеарны.

Найдем разложение вектора $a$ по базису $B(e),$ то есть найдем такое число $lambda$ что $a=lambda e:$

Ответ: $a=-2e.$

Домашнее задание.

2.28. Вне плоскости параллелограмма $ABCD$ взята точка $O.$ В базисе из векторов $overline, overline$ и $overline$ найти координаты:

а) вектора $overline$ , где $M$ точка пересечения диагоналей параллелограмма;

б) вектора $overline,$ где $K$- середина стороны $AD.$

Ответ: а) $(1/2; 0; 1/2);$ б) $(1, -1/2, 1/2).$

2.31. В треугольнике $ABC$ $overline=alphaoverline; overline=betaoverline;$ $overline=gammaoverline.$ Пусть $P, Q$ и $R -$ точки пересечения прямых $BF$ и $CK;$ $CK$ и $AM;$ $AM$ и $BF$ соответственно. В базисе из векторов $overline$ и $overline$ найти координаты векторов $overline,$ $overline$ и $overline.$

2.37. На плоскости заданы векторы $e_1(-1,2),$ $e_2(2,1)$ и $a(0,-2).$ Убедиться, что базис $B=e_1, e_2$ в множестве всех векторов на плоскости Построить заданные веткоры и найти разложение вектора $a$ по базису $B.$

Ответ: $a=-frace_1-frace_2.$

2.38. Показать, что тройка векторов $e_1(1,0,0), e_2(1,1,0)$ и $e_3(1,1,1)$ образуют базис в множестве всех векторов пространства. Вычислить координаты вектора $a=-2i-k$ в базисе $B(e_1, e_2, e_3)$ и написать соответствующее разложение вектора по базису.

Видео:Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Онлайн калькулятор. Разложение вектора по базису.

Этот онлайн калькулятор позволит вам очень просто разложить вектор по базисным векторам.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач и закрепить пройденый материал.

Видео:Разложение вектора по базису. 9 класс.Скачать

Калькулятор для разложения вектора по базисным векторам

Выберите размерность пространства

Количество координат в векторе:

Введите значение базисных векторов:

Введите значение вектора, который необходимо разложить по базису:

Инструкция использования калькулятора для разложение вектора по базисным векторам

Для того чтобы разложить вектор по базисным векторам онлайн:
выберите необходимую вам размерность пространства (количество координат в векторе);
введите значения базисных векторов;
введите значения вектора который нужно разложить по базису;
Нажмите кнопку «Разложить вектор по базису» и вы получите детальное решение задачи.

Ввод данных в калькулятор для разложение вектора по базисным векторам

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора разложение вектора по базисным векторам

Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 6Скачать

Теория. Разложение вектора по базису

Чтобы разложить, вектор b по базисным векторам a₁ , . a_n , необходимо найти коэффициенты x ₁, . x_n , при которых линейная комбинация векторов a₁ , . a_n равна вектору b .

Коэффициенты x ₁, . x_n будут координатами вектора b в базисе a₁ , . a_n .

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.