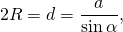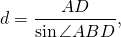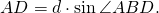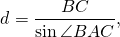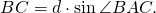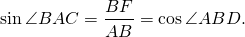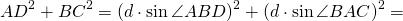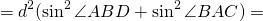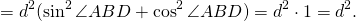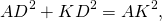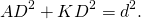Как доказать что диагональ вписанного четырехугольника является диаметром

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

Если диагонали вписанного четырехугольника перпендикулярны

Если диагонали вписанного четырехугольника перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности.

Дано:

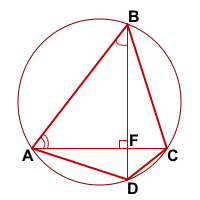
ABCD — вписанный четырёхугольник,

Доказать: AD² +BC² = d²

Радиус и диаметр описанной около треугольника окружности можно найти по формуле

где α — угол, противолежащий стороне a.

Для вписанного треугольника ABD

Для треугольника ABC —

Обозначим точку пересечения диагоналей четырёхугольника ABCD как F.

В прямоугольном треугольнике ABF по определению синуса и косинуса

Что и требовалось доказать.

Проведём диаметр AK, AK=d.

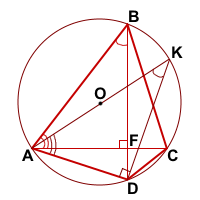
Рассмотрим треугольник ADK.

В прямоугольном треугольнике ABF ∠BAF=90°-∠ABF=90°-∠ABD=90°-∠AKD=∠KAD.

Таким образом, ∪KD=2∠KAD, ∪BC=2∠BAC, ∠BAC=∠KAD. Поэтому ∪KD=∪BC.

Так как дуги равны, то они стягивают равные хорды, то есть KD=BC.

Как доказать что четырехугольник вписан в окружность

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

«Описанная окружность» мы видели, что вокруг всякого треугольника можно описать окружность. То есть, для всякого треугольника найдётся такая окружность, что все три вершины треугольника «сидят» на ней. Вот так:

Вопрос: а можно ли то же самое сказать о четырехугольнике? Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника?

Вот оказывается, что это НЕПРАВДА! НЕ ВСЕГДА четырехугольник можно вписать в окружность. Есть очень важное условие:

Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна .

На нашем рисунке:

Посмотри, углы и лежат друг напротив друга, значит, они противоположные. А что же тогда с углами и ? Они вроде бы тоже противоположные? Можно ли вместо углов и взять углы и ?

Конечно, можно! Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет . Оставшиеся два угла тогда сами собой тоже дадут в сумме . Не веришь? Давай убедимся. Смотри:

Пусть . Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, . То есть — всегда! . Но , → .

Так что запомни крепко-накрепко:

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна

и наоборот:

Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.

Доказывать всё это мы здесь не будем (если интересно, заглядывай в следующие уровни теории). Но давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна .

Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма? Попробуем сперва «методом тыка».

Вот как-то не получается.

Теперь применим знание:

предположим, что нам как-то удалось посадить на параллелограмм окружность. Тогда непременно должно быть: , то есть .

А теперь вспомним о свойствах параллелограмма:

у всякого параллелограмма противоположные углы равны.

У нас получилось, что

А что же углы и ? Ну, то же самое конечно.

Получилось, что если параллелограмм вписан в окружность, то все его углы равны , то есть это прямоугольник!

И ещё при этом – центр окружности совпадает с точкой пересечения диагоналей этого прямоугольника. Это, так сказать, в качестве бонуса прилагается.

Ну, вот значит, выяснили, что параллелограмм, вписанный в окружность – прямоугольник.

А теперь поговорим о трапеции. Что будет, если трапецию вписать в окружность? А оказывается, будет равнобедренная трапеция. Почему?

Вот пусть трапеция вписана в окружность. Тогда опять , но из-за параллельности прямых и .

Значит, имеем: → → трапеция равнобокая.

Даже проще чем с прямоугольником, правда? Но запомнить нужно твёрдо – пригодиться: Трапеция, вписанная в окружность – равнобедренная.

Давай ещё раз перечислим самые главные утверждения, касающиеся четырехугольника, вписанного в окружность:

1. Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна
2. Параллелограмм, вписанный в окружность – непременно прямоугольник и центр окружности совпадает с точкой пересечения диагоналей
3. Трапеция, вписанная в окружность – равнобокая.

Вписанный четырехугольник. Средний уровень

Известно, что для всякого треугольника существует описанная окружность (это мы доказывали в теме «Описанная окружность»). Что же можно сказать о четырёхугольнике? Вот, оказывается, что НЕ ВСЯКИЙ четырехугольник можно вписать в окружность , а есть такая теорема:

Четырёхугольник вписан в окружность тогда и только тогда, когда сумма его противоположных углов равна .

На нашем рисунке –

Давай попробуем понять, почему так? Другими словами, мы сейчас докажем эту теорему. Но прежде чем доказывать, нужно понять, как устроено само утверждение. Ты заметил в утверждении слова «тогда и только тогда»? Такие слова означают, что вредные математики впихнули два утверждения в одно.

1. «Тогда» означает: Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна .
2. «Только тогда» означает: Если у четырёхугольника найдутся два противоположных угла, сумма которых равна , то такой четырехугольник можно вписать в окружность.

Прямо как у Алисы: «думаю, что говорю» и «говорю, что думаю».

А теперь разбираемся, отчего же верно и 1, и 2?

Пусть четырехугольник вписан в окружность. Отметим её центр и проведём радиусы и . Что же получится? Помнишь ли ты, что вписанный угол вдвое меньше соответствующего центрального? Если помнишь – сейчас применим, а если не очень – загляни в тему «Окружность. Вписанный угол» .

Получаем, что если – вписанный, то

Ну, и ясно, что и тоже в сумме составляет . (нужно так же рассмотреть и ).

Теперь и «наоборот», то есть 2.

Пусть оказалось так, что у четырехугольника сумма каких – то двух противоположных углов равна . Скажем, пусть

Мы пока не знаем, можем ли описать вокруг него окружность. Но мы точно знаем, что вокруг треугольника мы гарантированно окружность описать можем. Так и сделаем это.

Если точка не «села» на окружность, то она неминуемо оказалась или снаружи или внутри.

Рассмотрим оба случая.

Пусть сначала точка – снаружи. Тогда отрезок пересекает окружность в какой-то точке . Соединим и . Получился вписанный (!) четырехугольник .

Про него уже знаем, что сумма его противоположных углов равна , то есть , а по условию у нас .

Получается, что должно бы быть так, что .

Но это никак не может быть поскольку – внешний угол для и значит, .

А внутри? Проделаем похожие действия. Пусть точка внутри.

Тогда продолжение отрезка пересекает окружность в точке . Снова – вписанный четырехугольник , а по условию должно выполняться , но — внешний угол для и значит, , то есть опять никак не может быть так, что .

То есть точка не может оказаться ни снаружи, ни внутри окружности – значит, она на окружности!

Доказали всю-всю теорему!

Теперь посмотрим, какие же хорошие следствия даёт эта теорема.

Следствие 1

Параллелограмм, вписанный в окружность, может быть только прямоугольником.

Давай-ка поймём, почему так. Пусть параллелограмм вписан в окружность. Тогда должно выполняться .

Но из свойств параллелограмма мы знаем, что .

И то же самое, естественно, касательно углов и .

Вот и получился прямоугольник – все углы по .

Но, кроме того, есть ещё дополнительный приятный факт: центр окружности, описанной около прямоугольника, совпадает с точкой пересечения диагоналей.

Давай поймём почему. Надеюсь, ты отлично помнишь, что угол, опирающийся на диаметр – прямой.

а значит, – центр. Вот и всё.

Следствие 2

Трапеция, вписанная в окружность – равнобедренная.

Пусть трапеция вписана в окружность. Тогда .

Всё ли мы обсудили? Не совсем. На самом деле есть ещё один, «секретный» способ, как узнавать вписанный четырехугольник. Мы этот способ сформулируем не очень строго (но понятно), а докажем только в последнем уровне теории.

Если в четырёхугольнике можно наблюдать такую картинку, как здесь на рисунке (тут углы, «смотрящие» на сторону из точек и , равны), то такой четырехугольник – вписанный.

Это очень важный рисунок – в задачах часто бывает легче найти равные углы, чем сумму углов и .

Несмотря на совершенное отсутствие строгости в нашей формулировке, она верна, и более того, всегда принимается проверяющими ЕГЭ. Ты должен писать примерно так:

« — вписанный» — и всё будет отлично!

Не забывай этот важный признак – запомни картинку, и, возможно, она тебе вовремя бросится в глаза при решении задачки.

Вписанный четырехугольник. Краткое описание и основные формулы

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна

Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.

Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна .

Параллелограмм, вписанный в окружность – непременно прямоугольник , и центр окружности совпадает с точкой пересечения диагоналей.

Трапеция , вписанная в окружность – равнобокая .

P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это — не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время.

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Я рекомендую использовать для этих целей наш учебник «YouClever» (который ты сейчас читаешь) и решебник и программу подготовки «100gia».

Условия их приобретения изложены здесь. Кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!

И в заключение.

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Комментарии

спасибо очень интересно почему авторы учебников не пишут это

Спасибо, Ольга. Автори интересных учебников пишут. Просто их не так много)

Хотелось бы поблагодарить составителей статьи: подача материала очень интересна и необычна, и сам он легко усваивается!

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

«Описанная окружность» мы видели, что вокруг всякого треугольника можно описать окружность. То есть, для всякого треугольника найдётся такая окружность, что все три вершины треугольника «сидят» на ней. Вот так:

Вопрос: а можно ли то же самое сказать о четырехугольнике? Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника?

Вот оказывается, что это НЕПРАВДА! НЕ ВСЕГДА четырехугольник можно вписать в окружность. Есть очень важное условие:

Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна .

На нашем рисунке:

Посмотри, углы и лежат друг напротив друга, значит, они противоположные. А что же тогда с углами и ? Они вроде бы тоже противоположные? Можно ли вместо углов и взять углы и ?

Конечно, можно! Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет . Оставшиеся два угла тогда сами собой тоже дадут в сумме . Не веришь? Давай убедимся. Смотри:

Пусть . Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, . То есть — всегда! . Но , → .

Так что запомни крепко-накрепко:

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна

и наоборот:

Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.

Доказывать всё это мы здесь не будем (если интересно, заглядывай в следующие уровни теории). Но давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна .

Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма? Попробуем сперва «методом тыка».

Вот как-то не получается.

Теперь применим знание:

предположим, что нам как-то удалось посадить на параллелограмм окружность. Тогда непременно должно быть: , то есть .

А теперь вспомним о свойствах параллелограмма:

у всякого параллелограмма противоположные углы равны.

У нас получилось, что

А что же углы и ? Ну, то же самое конечно.

Получилось, что если параллелограмм вписан в окружность, то все его углы равны , то есть это прямоугольник!

И ещё при этом – центр окружности совпадает с точкой пересечения диагоналей этого прямоугольника. Это, так сказать, в качестве бонуса прилагается.

Ну, вот значит, выяснили, что параллелограмм, вписанный в окружность – прямоугольник.

А теперь поговорим о трапеции. Что будет, если трапецию вписать в окружность? А оказывается, будет равнобедренная трапеция. Почему?

Вот пусть трапеция вписана в окружность. Тогда опять , но из-за параллельности прямых и .

Значит, имеем: → → трапеция равнобокая.

Даже проще чем с прямоугольником, правда? Но запомнить нужно твёрдо – пригодиться: Трапеция, вписанная в окружность – равнобедренная.

Давай ещё раз перечислим самые главные утверждения, касающиеся четырехугольника, вписанного в окружность:

1. Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна
2. Параллелограмм, вписанный в окружность – непременно прямоугольник и центр окружности совпадает с точкой пересечения диагоналей
3. Трапеция, вписанная в окружность – равнобокая.

Вписанный четырехугольник. Средний уровень

Известно, что для всякого треугольника существует описанная окружность (это мы доказывали в теме «Описанная окружность»). Что же можно сказать о четырёхугольнике? Вот, оказывается, что НЕ ВСЯКИЙ четырехугольник можно вписать в окружность , а есть такая теорема:

Четырёхугольник вписан в окружность тогда и только тогда, когда сумма его противоположных углов равна .

На нашем рисунке –

Давай попробуем понять, почему так? Другими словами, мы сейчас докажем эту теорему. Но прежде чем доказывать, нужно понять, как устроено само утверждение. Ты заметил в утверждении слова «тогда и только тогда»? Такие слова означают, что вредные математики впихнули два утверждения в одно.

1. «Тогда» означает: Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна .
2. «Только тогда» означает: Если у четырёхугольника найдутся два противоположных угла, сумма которых равна , то такой четырехугольник можно вписать в окружность.

Прямо как у Алисы: «думаю, что говорю» и «говорю, что думаю».

А теперь разбираемся, отчего же верно и 1, и 2?

Пусть четырехугольник вписан в окружность. Отметим её центр и проведём радиусы и . Что же получится? Помнишь ли ты, что вписанный угол вдвое меньше соответствующего центрального? Если помнишь – сейчас применим, а если не очень – загляни в тему «Окружность. Вписанный угол» .

Получаем, что если – вписанный, то

Ну, и ясно, что и тоже в сумме составляет . (нужно так же рассмотреть и ).

Теперь и «наоборот», то есть 2.

Пусть оказалось так, что у четырехугольника сумма каких – то двух противоположных углов равна . Скажем, пусть

Мы пока не знаем, можем ли описать вокруг него окружность. Но мы точно знаем, что вокруг треугольника мы гарантированно окружность описать можем. Так и сделаем это.

Если точка не «села» на окружность, то она неминуемо оказалась или снаружи или внутри.

Рассмотрим оба случая.

Пусть сначала точка – снаружи. Тогда отрезок пересекает окружность в какой-то точке . Соединим и . Получился вписанный (!) четырехугольник .

Про него уже знаем, что сумма его противоположных углов равна , то есть , а по условию у нас .

Получается, что должно бы быть так, что .

Но это никак не может быть поскольку – внешний угол для и значит, .

А внутри? Проделаем похожие действия. Пусть точка внутри.

Тогда продолжение отрезка пересекает окружность в точке . Снова – вписанный четырехугольник , а по условию должно выполняться , но — внешний угол для и значит, , то есть опять никак не может быть так, что .

То есть точка не может оказаться ни снаружи, ни внутри окружности – значит, она на окружности!

Доказали всю-всю теорему!

Теперь посмотрим, какие же хорошие следствия даёт эта теорема.

Следствие 1

Параллелограмм, вписанный в окружность, может быть только прямоугольником.

Давай-ка поймём, почему так. Пусть параллелограмм вписан в окружность. Тогда должно выполняться .

Но из свойств параллелограмма мы знаем, что .

И то же самое, естественно, касательно углов и .

Вот и получился прямоугольник – все углы по .

Но, кроме того, есть ещё дополнительный приятный факт: центр окружности, описанной около прямоугольника, совпадает с точкой пересечения диагоналей.

Давай поймём почему. Надеюсь, ты отлично помнишь, что угол, опирающийся на диаметр – прямой.

а значит, – центр. Вот и всё.

Следствие 2

Трапеция, вписанная в окружность – равнобедренная.

Пусть трапеция вписана в окружность. Тогда .

Всё ли мы обсудили? Не совсем. На самом деле есть ещё один, «секретный» способ, как узнавать вписанный четырехугольник. Мы этот способ сформулируем не очень строго (но понятно), а докажем только в последнем уровне теории.

Если в четырёхугольнике можно наблюдать такую картинку, как здесь на рисунке (тут углы, «смотрящие» на сторону из точек и , равны), то такой четырехугольник – вписанный.

Это очень важный рисунок – в задачах часто бывает легче найти равные углы, чем сумму углов и .

Несмотря на совершенное отсутствие строгости в нашей формулировке, она верна, и более того, всегда принимается проверяющими ЕГЭ. Ты должен писать примерно так:

« — вписанный» — и всё будет отлично!

Не забывай этот важный признак – запомни картинку, и, возможно, она тебе вовремя бросится в глаза при решении задачки.

Вписанный четырехугольник. Краткое описание и основные формулы

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна

Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.

Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна .

Параллелограмм, вписанный в окружность – непременно прямоугольник , и центр окружности совпадает с точкой пересечения диагоналей.

Трапеция , вписанная в окружность – равнобокая .

P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это — не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время.

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Я рекомендую использовать для этих целей наш учебник «YouClever» (который ты сейчас читаешь) и решебник и программу подготовки «100gia».

Условия их приобретения изложены здесь. Кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!

И в заключение.

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Комментарии

спасибо очень интересно почему авторы учебников не пишут это

Спасибо, Ольга. Автори интересных учебников пишут. Просто их не так много)

Хотелось бы поблагодарить составителей статьи: подача материала очень интересна и необычна, и сам он легко усваивается!

🔍 Видео