Как доказать что четырехугольник прямоугольник по векторам

Видео:Задание 25 Доказать, что четырёхугольник прямоугольник Определение прямоугольникаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Задачник «Векторный метод решения задач»

Составила: Казакова Ольга Сергеевна,

учитель математики МОУ «СОШ № 75» г. Саратова.

Данный задачник предназначен для изучения тем: «Векторы», «Действия с векторами», «Векторный метод решения задач». Инструктивное изложение материала, при постоянной практической пробе, даёт возможность изучить темы самостоятельно.

№ 1.Заполните таблицу. Основные понятия.

Решение и изображение

1)На плоскости отметьте точки A и B , постройте отрезок AB ;

2)На отрезке AB пусть точка A будет началом, а точка B – концом. Укажите стрелкой в конце отрезка направление из начала в конец. Вы получили отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, то есть получили направленный отрезок или вектор .

3)Построен вектор , его можно обозначить и однострочной латинской буквой, например, , которая записывается над изображением вектора.

Сколько векторов можно провести, выбирая начало и конец среди данных на плоскости:

2)трёх точек, не лежащих на одной прямой;

3)четырёх точек, не лежащих на одной прямой?

Отметьте на плоскости любую точку и обозначьте её, например, заглавной буквой M . Вы построили нулевой вектор, его начало и конец совпадают.

Обозначение нулевого вектора: или символом .

1)Постройте отрезок AB , длина которого 4 см;

2)Постройте вектор .

Длиной или модулем ненулевого вектора называется длина отрезка AB .

Обозначение: = AB = 4.

Чему равна длина нулевого вектора?

3)Постройте вектор , длиной 7 см.

1)Постройте параллельные прямые p и m .

2)На прямой p постройте:

а)вектор , произвольной длины и направления;

б)вектор , произвольной длины и направления;

3)На прямой m постройте: вектор , произвольной длины и направления.

Ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых.

Нулевой вектор считается коллинеарным любому вектору.

4)Выпишите попарно коллинеарные векторы.

5)Постройте и обозначьте два произвольных вектора, которые являются не коллинеарными вектору . Будут ли они являться коллинеарными векторам , ?

Постройте два коллинеарных вектора.

Полученные векторы направлены одинаково или противоположно?

Если одинаково, то вы построили сонаправленные векторы. Обозначение:

 .

Если противоположно, то вы построили противоположно направленные векторы. Обозначение:  .

Начертите параллелограмм ABCD . Проведите векторы, начало и конец которых совпадают с какими-то двумя вершинами параллелограмма. Сколько существует пар векторов, которые являются:

1)коллинеарными друг другу;

Постройте векторы и , так, чтобы:

1)  ;

2) .

Вы построили равные векторы.

Векторы называются равными , если они сонаправлены и их длины равны.

№ 2.Заполните таблицу. Операции над векторами.

Решение и изображение

На плоскости произвольно выберите точку A , приняв её за начало, проведите вектор , произвольной длины и направления. Таким образом, вы отложили вектор от точки A .

Можно отложить от другой точки плоскости, вектор, равный данному вектору ?

Допустим, что вектор ненулевой, а точки A и B – его начало и конец.

1)Через произвольно взятую точку M плоскости проведите прямую p , параллельную AB (если M – точка прямой AB , то в качестве прямой p возьмём саму прямую AB ).

2)На прямой p отложите два противоположно направленных вектора и , длины которых равны отрезку AB .

Среди построенных векторов выберите тот, что сонаправлен с вектором , он и будет являться искомым вектором, равным вектору . К тому же такой вектор только один, что следует из построения.

А если вектор – нулевой? Ответьте самостоятельно.

Итак, от любой точки M можно отложить вектор, равный данному вектору , и при том только один.

1)Векторы и .

2)Произвольная точка A .

3)От точки A отложите вектор , равный вектору .

4)От точки B отложите вектор , равный вектору .

5)Вектор .

Вы, таким образом, выполнили построение сложения векторов и по правилу треугольника . Вектор называется суммой векторов и .

Докажем, что если и , то .

Рассмотрим случай, когда точки A , B , , точки B , C , и точки A , C , не лежат на одной прямой (остальные случаи рассмотрите самостоятельно).

а) ;

б) ;

в)Соединим точки A и , B и , C и ;

2)  – параллелограмм  ;

3)  – параллелограмм  ;

4)Из 2) и 3)   – параллелограмм;

5)Значит, . Доказано.

Вывод: при необходимости можно работать как с данными векторами, так и с равными им.

Законы сложения векторов.

Для любых векторов , и справедливы равенства:

(переместительный закон)

(сочетательный закон)

Доказательство законов проведите самостоятельно, опираясь на подсказки:

Для доказательства первого закона можете достроить треугольник до параллелограмма и работать как с самими векторами, так и с равными им.

Для доказательства второго закона достаточно несколько раз применить правило треугольника для сложения векторов, последовательно отложенных от концов предыдущих векторов.

1)Произвольная точка A ;

2)Неколлинеарные векторы и ;

3) От точки A отложите вектор , равный вектору .

4)От точки A отложите вектор , равный вектору .

5)Постройте параллелограмм ABCD ;

6) .

Вы построили сложение векторов и по правилу параллелограмма сложения неколлинеарных векторов.

Как сложить несколько векторов?

Последовательное применение правила треугольника для сложения векторов даёт возможность сложить любое количество векторов. Причём порядок сложения не важен. Сложение нескольких векторов производится следующим образом: два вектора складываются, получившаяся сумма складывается с третьим и т.д.

Выполните сложение пяти любых векторов, используя то, что несколько векторов можно расположить таким образом: первый вектор откладывается от любой точки, второй – от конца первого и т.д. Сумма всех векторов – вектор, направленный от начала первого вектора к концу последнего.

Вы выполнили построение сложения нескольких векторов, пользуясь правилом многоугольника .

Подумайте, чему будет равна сумма векторов, если начало первого вектора совпадает с концом последнего?

Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .

Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены. Обозначение: . .

Докажите, что . Для этого воспользуйтесь определением разности векторов и прибавлением к обеим частям равенства вектора.

На прямой p от любой точки O отложите вектор , от конца вектора отложите вектор . Длина построенного суммарного вектора, равна или .

Произведением ненулевого вектора на число k называется такой вектор , длина которого равна , причём векторы и сонаправлены при k  0 и противоположно направлены при k .

Произведением нулевого вектора на любое число считается нулевой вектор.

Из определения следует:

1)произведение любого вектора на число нуль есть нулевой вектор;

2)для любого числа k и любого вектора векторы и коллинеарны.

Свойства умножения вектора на число.

Для любых чисел k , l и любых векторов , справедливы равенства:

(сочетательный закон)

(первый распределительный закон)

(второй распределительный закон)

На прямой p от произвольно выбранной точки O отложите: вектор , длиной 1 см; вектор , сонаправленный с вектором , длиной 2 см; вектор , противоположно направленный с вектором , длиной 3 см.

Попробуем выразить векторы и через вектор .

Во сколько раз длины этих векторов отличаются от длины вектора ?

; ;

 ,  , т. е. векторы , и коллинеарны друг другу, значит, можно воспользоваться леммой.

Если векторы и коллинеарны и , то существует такое число k , что .

Итак, можем выразить: , .

От произвольной точки O отложите векторы и , и – произвольные данные векторы. Если и не являются сонаправленными, то лучи OA и OB образуют угол AOB , градусную меру которого обозначьте буквой α. Будем говорить, что угол между векторами и равен α. Обозначение: .

Если  , то

Если , то векторы и называются перпендикулярными.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Напишите формулу скалярного произведения для случаев, когда:

;

;

.

Сделайте вывод, о том, в каком случае скалярное произведение двух векторов равно нулю.

Напишите формулу скалярного произведения для случая, когда вектор скалярно умножается на себя. В этом случае скалярное произведение называется скалярным квадратом . Обозначение: .

Итак, перечислите все операции над векторами.

№ 3.Решая задачи, заполните пустые ячейки в таблице.

k , что ,

точки M и N совпадают

точка C принадлежит прямой AB

, или
, или

точка С – середина отрезка AB

точка D разбивает отрезок AC так, что AD : DC = m : n

Заполняя таблицу, вы пользовались векторным методом решения задач.

Векторный метод – один из наиболее общих методов решения геометрических задач.

Для решения задач элементарной геометрии с помощью векторов необходимо, прежде всего, научиться «переводить» условие геометрической задачи на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык. В этом и состоит сущность векторного метода решения геометрических задач.

Далее вам необходимо самостоятельно решать задачи. После решения каждой задачи делайте вывод о её значимости. Если результат задачи возможно использовать для решения других, то заносите его в таблицу № 3. Таким образом, вы получите набор базовых задач, на основании которых решаются более сложные.

1)Докажите, что средняя линия треугольника параллельна его третьей стороне и равна её половине.

2)Докажите, что средняя линия трапеции параллельна её основанию и её длина равна полусумме длин её оснований.

3)Если средняя линия четырёхугольника равна полусумме длин её оснований (сторон, не имеющих общей точки со средней линией), то этот четырёхугольник является трапецией или параллелограммом.

4)Около окружности описана равнобочная трапеция ABCD . Точки E и K – точки касания этой окружности с боковыми сторонами AB и CD . Докажите, что отрезок EK параллелен основаниям трапеции.

5)Докажите, что биссектриса угла треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам. Выразите биссектрису через угол треугольника, который она делит пополам, и через стороны этого угла.

6)Если точки M и N делят отрезки AB и CD соответственно в равных отношениях так, что AM : MB = CN : ND = m : n , то выполняется равенство: .

7)В треугольнике ABC через M обозначена точка пересечения медиан. Докажите, что .

8)Пусть M – точка пересечения медиан треугольника ABC , O – произвольная точка. Докажите, что .

9)Пусть H – точка пересечения высот треугольника ABC , O – центр описанной окружности. Докажите, что .

10)Докажите, что три точки A , B , C ( A ≠ B ) лежат на одной прямой тогда и только тогда, когда имеет место равенство, , в котором α+β=1, где O – некоторая точка.

11)Докажите, что центр описанной окружности

12)Докажите, что если точки пересечения диагоналей четырёхугольника и середины двух его противоположных сторон лежат на одной прямой, то этот четырёхугольник – трапеция или параллелограмм.

13)Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

14)Докажите, что биссектрисы треугольника пересекаются в одной точке.

15)Докажите, что высоты треугольника пересекаются в одной точке.

16)Докажите, что четырёхугольник является параллелограммом тогда и только тогда, когда его диагонали в точке пересечения делятся пополам.

17)Докажите, что в произвольном четырёхугольнике средние линии (т. е. отрезки, соединяющие середины противоположных сторон) точкой их пересечения делятся пополам.

18)Найти косинус угла между диагоналями прямоугольника, стороны которого равны a и b .

19)Докажите, что диагонали ромба взаимно перпендикулярны.

20)Докажите, что вписанный угол, опирающийся на диаметр окружности, — прямой.

21)Докажите, что если в треугольнике длины его сторон a , b , c связаны соотношением , то угол этого треугольника, лежащий против стороны длины c , — прямой.

22)Даны стороны a , b , c треугольника. Найдите медианы , , , проведённые к этим сторонам.

23)В треугольнике со сторонами a , b , c найти длину высоты , опущенную на сторону c .

24)В треугольнике со сторонами a , b , c найти длину биссектрисы , проведённой к стороне c .

25)Докажите, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон.

26)Докажите, что сумма квадратов длин диагоналей трапеции равна сумме квадратов длин её боковых сторон плюс удвоенное произведение длин оснований.

27)Доказать, что большей медиане треугольника соответствует меньшая сторона и обратно.

28)Докажите, диагонали прямоугольника равны между собой.

29)Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности.

30)В четырёхугольнике ABCD прямая, проведённая через вершину A параллельна стороне BC , пересекает диагональ BD в точке M , а прямая проведённая через вершину B параллельно стороне AD , пересекает диагональ AC в точке N . Докажите, что MN || DC .

31)Четыре окружности радиуса R пересекаются по три в точках M и N , и по две в точках A , B , C , D . Докажите, что ABCD – параллелограмм.

32)Пусть K , L , M , N – середины отрезков AB , BC , CD , DE пятиугольника ABCDE , а точки P и Q – середины отрезков KM и LN соответственно. Докажите, что отрезок PQ в четыре раза меньше стороны AE и параллелен ей.

33)В плоскости даны четырёхугольник ABCD и точка M . Докажите, что точки, симметричные точке M относительно середин сторон этого четырёхугольника, являются вершинами параллелограмма.

34)На диагоналях AC и CE правильного шестиугольника ABCDEF взяты точки M и N соответственно, такие, что AM : AC = CN : CE = λ. Известно, что точки B , M , N лежат на одной прямой. Найдите λ.

35)Дан параллелограмм ABCD ( AD || BC , AB || CD ). На стороне AD выбрана точка K , а на AC – точка L так, что 5 AK = AD , 6 AL = AC . Докажите, что KL || BL и найдите отношение их длин.

36)Точки M и K на сторонах AB и BC треугольника ABC таковы, что AM : MB =3:4, CK : KB =2:3. Отрезки AK и CM пересекаются в точке N . Найдите отношение AN : NK .

37)Точка K на стороне AC и точки L , M на стороне BC треугольника ABC таковы, что AK : KC = CL : LB = BM : MC =1:2, N – середина стороны AC . Найти отношение, в котором точка пересечения отрезков KL и MN делит отрезок KL .

38)Через середину E медианы треугольника ABC проведена прямая AE , пересекающая сторону BC в точке F . Вычислить: AE : EF и CF : FB .

39)Дан параллелограмм ABCD . Точка M делит сторону AD в отношении p , т. е. AM : MD = p ; точка N делит сторону DC в отношении q , т. е. DN : NC = q . Прямые BM и AN пересекаются в точке S . Вычислить отношения AS : SN и BS : SM .

40)В параллелограмме ABCD сторона AD разделена на n равных частей и первая точка деления M (считая от A ) соединена с B . В каком отношении делит точка N диагональ AC и отрезок MB ?

41)В треугольнике ABC проведена медиана CM . Прямая l пересекает отрезки CA , CM , CB в точках , , соответственно. Докажите равенство .

42)На сторонах AC и BC треугольника ABC взяты точки M и D так, что AM = AC , BD = BC , а на прямой AD – точка N так, что AN = AD . Доказать, что точки M , N и B лежат на одной прямой. Какую часть от отрезка MB составляет отрезок MN ?

43)На стороне AD и диагонали AC параллелограмма ABCD взяты точки M и N так, что AM = AD , AN = AC . Доказать, что точки M , N и B лежат на одной прямой. В каком отношении делит точка N отрезок MB ?

44)На стороне AB треугольника ABC дана точка P , через которую проведены прямые параллельно его медианам A и A и пересекающие соответственно стороны треугольника в точках и . Докажите, что середина отрезка (точка E ), а также точка P и точка G пересечения медиан треугольника лежат на одной прямой и найдите отношение длин отрезков EG и EP .

45)Докажите, что точки пересечения диагоналей трапеции, боковых сторон, а также середины оснований лежат на одной прямой.

46)Через точку P – внутреннюю точку параллелограмма ABCD – проведены прямая KM || AD и прямая LN || AB , пересекающие стороны AB , BC , CD , DA параллелограмма в точках K , L , M , N соответственно. Q – точка пересечения средних линий четырёхугольника KLMN , S – точка пересечения диагоналей параллелограмма ABCD . Докажите, что Q – середина отрезка PS .

47)Пусть , , – середины сторон BC , AC , AB треугольника ABC . Доказать, что точки пересечения медиан треугольника ABC и треугольника совпадают.

48)Пусть ABCDEF – произвольный шестиугольник и U , V , W , X , Y , Z – середины его сторон. Докажите, что центры тяжести (т. е. точки пересечения медиан) треугольника UWY и треугольника VXZ совпадают.

49)Докажите, что прямая, соединяющая середины оснований трапеции, и продолжения боковых сторон трапеции пересекаются в одной точке.

50)На сторонах параллелограмма заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки деления служат вершинами параллелограмма, а центры этих параллелограммов совпадают.

51)На сторонах треугольника заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки пересечения медиан данного треугольника и треугольника, имеющего вершинами точки деления, совпадают.

52)В треугольнике ABC длины сторон связаны соотношением . Докажите, что медианы, проведённые к сторонам AC и BC , взаимно перпендикулярны.

53)Найдите косинус угла между медианами прямоугольного равнобедренного треугольника, проведёнными к его катетам.

54)Найти косинус угла между медианами равнобедренного треугольника, проведёнными к его боковым сторонам, при условии, что угол при вершине равен α.

55)Найти косинус угла при вершине равнобедренного треугольника, если медианы, проведённые к его боковым сторонам, а) перпендикулярны; б) образую угол .

56)В треугольнике две стороны равны 2 и 4, а угол между ними равен . Найти угол ψ между короткой стороной и медианой, проведённой к третьей стороне.

57)В окружности с центром O радиуса r вписан четырёхугольник ABCD . Доказать, что если , то диагонали четырёхугольника взаимно перпендикулярны.

58)В прямоугольнике ABCD опущен перпендикуляр BK на диагональ AC . Точки M и N – середины отрезков AK и CD соответственно. Докажите, что угол BMN прямой.

59)На стороне AB треугольника ABC с углом ABC , равным α , расположена точка K , причём AK = BC . Пусть P – середина BK , M – середина AC . Найдите угол APM .

60)Точка K – середина стороны AB квадрата ABCD , а точка M лежит на диагонали AC , причём AM : MC = 3 : 1. Докажите, что угол KMD равен .

61)На сторонах AB и AC треугольника ABC во внешнюю сторону построены квадраты AMNB и CKLA . Докажите, что медиана AP треугольника ABC перпендикулярна прямой ML .

62)На стороне AB треугольника ABC дана точка D . Выразить расстояние CD через длины сторон данного треугольника a , b , c и расстояния AD = m и DB = n .

63)Выразить расстояние от заданной точки O до точки M пересечения медиан треугольника ABC через длины сторон треугольника BC = a , AC = b , AB = c и расстояния от точки O до вершин треугольника OA = , OB = , OC = .

64)В параллелограмме ABCD точка K – середина стороны BC , а точка M – середина стороны CD . Найдите AD , если AK = 6, AM = 3,  KAM = .

Список использованной литературы

Атанасян Л.С. и др. Геометрия. Учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 2003.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2009.

Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Шестаков С.А., Юдина И.И. Планиметрия. Пособие для углубленного изучения математики – М.: ФИЗМАТЛИТ, 2005.

Василевский А.Б. Методы решения геометрических задач. – Минск: Вышэйш. школа, 1965.

Габович И.Г. Алгоритмический подход к решению геометрических задач. – М.: Просвещение, 1996.

Гордин Р.К. Геометрия. Планиметрия 7-9 кл. – М.: МЦНМО, 2006.

Готман Э.Г., Скопец З.А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9 и 10 кл. – М.: Просвещение, 1979.

Гусев В. А. и др. Практикум по элементарной математике: Геометрия: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов и учителей. – М.: Просвещение, 1992.

Зеленяк О. П. Решение задач по планиметрии. Технология алгоритмического подхода на основе задач-теорем. Моделирование в среде Turbo Pascal. – Киев, Москва: ДиаСофтЮП, ДМК Пресс, 2008.

Шарыгин И. Ф. Геометрия. 7 – 9 кл.: Учеб. для общеобразоват. учеб. завед. – М.: Дрофа, 2001.

Шарыгин И.Ф. Решение задач: Учеб. пособие для 10 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.

Шестаков С. А. Векторы на экзаменах. Векторный метод в стереометрии. – М.: МЦНМО, 2005.

Видео:№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Докажите что векторы ABCD ПРЯМОУГОЛЬНИК?

Геометрия | 5 — 9 классы

Докажите что векторы ABCD ПРЯМОУГОЛЬНИК.

А(0 ; — 3)В( — 1 ; 0)С(5 ; 2)D(6 ; — 1).

В прямоугольнике противоположные стороны равны.

Посмотрим равны листороны — АВ и СД.

Вектор АВ = (0 — ( — 1)) и ( — 3 — 0) = (1 ; — 3).

Вектор СД = (6 — 5) и ( — 1 — 2) = (1 ; — 3).

Вектор АВ = СД, , , , значит, это прямоугольник.

Можна таким же образом доказать равенство векторов ВС = АД.

Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

В прямоугольнике ABCD AB = 3 см, BC = 4 см?

В прямоугольнике ABCD AB = 3 см, BC = 4 см.

Найдите длину вектора AC.

Видео:ОГЭ Задание 25 Доказать что четырехугольник квадратСкачать

Какое правило для сложения векторов выражает равенство вектор BD = вектор BC + вектор BA?

Какое правило для сложения векторов выражает равенство вектор BD = вектор BC + вектор BA.

Притом, что ABCD — прямоугольник?

Видео:Прямоугольник. 8 класс.Скачать

Докажите , что если в параллелограмме ABCD углы ABD и BAC равны , то этот параллелограмм — прямоугольник?

Докажите , что если в параллелограмме ABCD углы ABD и BAC равны , то этот параллелограмм — прямоугольник.

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Среди векторов , определенных сторонами прямоугольника ABCD , найдите : 1) коллинеарные ; 2) перпендикулярные ; 3) равные между собой векторы?

Среди векторов , определенных сторонами прямоугольника ABCD , найдите : 1) коллинеарные ; 2) перпендикулярные ; 3) равные между собой векторы.

Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать

В прямоугольнике ABCD BD — диагональ?

В прямоугольнике ABCD BD — диагональ.

Докажите, что треугольник ABD = треугольнику BCD.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Выражение скалярного произведения через координаты векторов даны точки А(1 ; 1), B(4 ; 4), C(0 ; 4), D( — 4 ; 4)?

Выражение скалярного произведения через координаты векторов даны точки А(1 ; 1), B(4 ; 4), C(0 ; 4), D( — 4 ; 4).

Докажите что четехуголник ABCD — ПРЯМОУГОЛЬНИК.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Дан квадрат ABCD ?

Дан квадрат ABCD .

Докажите равенство векторов BC и AD и объясните почему не равны векторы AB и BC.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Докажите что прямоугольник ABCD и треугольник AKD изображенные на рис?

Докажите что прямоугольник ABCD и треугольник AKD изображенные на рис.

Видео:Какой четырехугольник называется прямоугольником. Геометрия 8 класс. Глава 5Скачать

В четырехугольнике ABCD известно, что вектор ВС = — векторDA?

В четырехугольнике ABCD известно, что вектор ВС = — векторDA.

Докажите, что этот четырехугольник — параллелограмм.

Видео:8 класс, 7 урок, ПрямоугольникСкачать

Дан прямоугольник ABCD?

Дан прямоугольник ABCD.

X — произвольная точка на плоскости.

Докажите что сумма векторов XA + XC = XB + XD.

Вы открыли страницу вопроса Докажите что векторы ABCD ПРЯМОУГОЛЬНИК?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Решение смотри на фотографии.

Возможны 2 случая : 1) Внешний угол при вершине равнобедренного треугольника равен 110°. Тогда смежный к нему угол равен 180 — 110 = 70°. Сумма углов при основании треугольника равна 180 — 70 = 110°, а каждый из углов при основании равнобедренного ..

1. Пусть один градус данного угла = х , тогда составим уравнение 2х + 3х + 7х = 180 12х = 180 х = 15 2 * 15 = 30 градусов 3 * 15 = 45 градусов 7 * 15 = 105 градусов. Ответ : 30, 45, 105 2. Пусть один градус данного угла = х , тогда составим уравнен..

1. Так как треугольники АВС и МNP равны, то их елементы тоже равные. Значит : ВС = NP = 12см угол С = углу Р = 121° 2. Нет, не могут , потому что MNP имеет разные по длинне стороны.

Так как у квадрата все стороны равны, а их диагонали при пересечении образуют перпендикуляр, то можно сделать вывод, что полученный четырехугольник — квадрат, а квадрата все стороны равны. Значит ВС = ВД ч. Т. д.

BC + AD = 3 + 4 = 7cm = 7 + 7 = 14cm AB + CD = 14 : 2 = 7cm P = 14 + 7 = 21 cm.

ВА = ВС , ∠В Общий(по условию) ∠ВАЕ = ∠ВСД, так как∠1 = ∠2⇒ треугольники АВЕ и ВСД равны по 2 углам и стороне значит АЕ = СД.

А B = 77 + 8 = 85, А B = 85 треуг АBH : BH = AB AH = 85 — 77 = 1296, BH = 36 — высота ромба S = AD * BH = 85 * 36 = 3060.

Треугольники ABD и BCD подобны, т. К. у них равные углы. Один угол 90, угол BAD = 90 — ABD = DBC Из подобия вытекает AD / BD = BD / DC 9 / BD = BD / 16 BD ^ 2 = 16 * 9 BD = 4 * 3 = 12.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Четырехугольники

теория по математике 📈 планиметрия

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Определение

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.

Видео:Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

Виды и свойства выпуклых четырехугольников

Сумма углов выпуклого четырехугольника равна 360 градусов.

Прямоугольник

Прямоугольник – это четырехугольник, у которого все углы прямые.

На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь

1. Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
2. Диагонали прямоугольника равны (АС=ВD).
3. Диагонали пересекаются и точкой пересечения делятся пополам.
4. Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
5. Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:

S=ab, где a и b соседние стороны прямоугольника.

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны.

Свойства квадрата

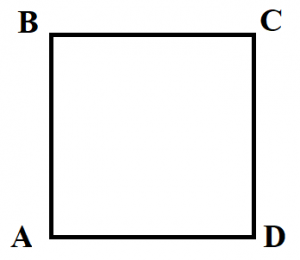
1. Диагонали квадрата равны (BD=AC).
2. Диагонали квадрата пересекаются под углом 90 градусов.
3. Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
4. Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
5. Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция

Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций

Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов

Средняя линия трапеции

Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.

Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.

По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17

Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).

Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .

Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула

S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63

pазбирался: Даниил Романович | обсудить разбор | оценить

Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить

Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8

Для выполнения данного задания надо подставить все известные данные в формулу:

12,8= d 1 × 16 × 2 5 . . 2 . .

В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .

Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2

Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4

pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

Задание №1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.

Решение

Для решения 1 задачи работаем с текстом и планом одновременно:

при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.

Итак, получили следующее:

1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.

Заполняем нашу таблицу:

Записываем ответ: 3517

Задание №2

Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

Решение

Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.

Задание №3

Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4

Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.

Решение

Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м

Задание №5

Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?

Решение

Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:

1 магазин: 232х0,25=58 кг

2 магазин: 232х0,4=92,8 кг

Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:

1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)

2 магазин: 92,8:5=18,56; значит надо 19 банок.

Вычислим стоимость краски в каждом магазине плюс доставка:

1 магазин: 10х3000+500=30500 руб.

2 магазин: 19х1900+800=36900 руб.

Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

💥 Видео

Задача, которую боятсяСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать